- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Выполнение логических операций
Содержание
- 1. Презентация по теме Выполнение логических операций
- 2. Логическая операция – способ построения
- 3. Инверсия (логическое отрицание) Инверсия логической переменной истина,
- 4. Таблица истинности
- 5. Конъюнкция (логическое умножение) Конъюнкция двух логических
- 6. Таблица истинности
- 7. Дизъюнкция (логическое сложение) Дизъюнкция
- 8. Таблица истинности
- 9. Импликация (логическое следование) Импликация двух логических
- 10. Таблица истинности
- 11. Эквивалентность (логическое равенство) Эквивалентность двух
- 12. Таблица истинности
- 13. Приоритет выполнения логических операций При
- 14. ПримерДана формулаОпределите порядок вычисления. Порядок вычисления:Инверсия – Конъюнкция –Дизъюнкция – Импликация – Эквивалентность –
Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Слайд 2 Логическая операция – способ построения сложного высказывания из данных
высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
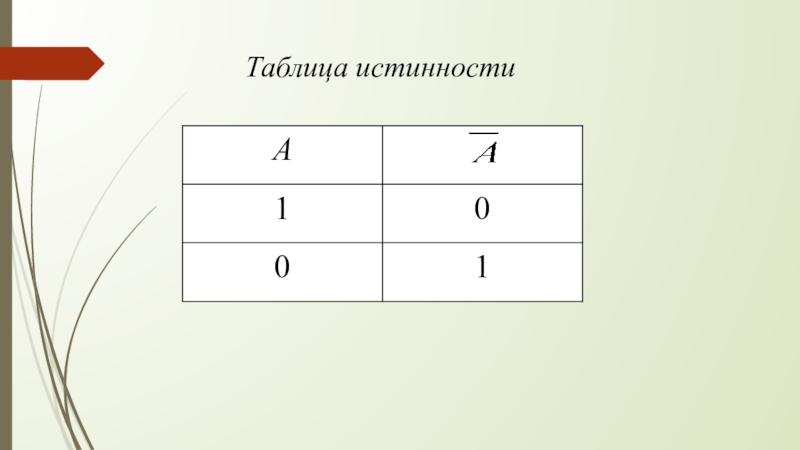
Слайд 3Инверсия (логическое отрицание)
Инверсия логической переменной истина, если переменная ложна, и,
наоборот, инверсия ложна, если переменная истинна.
Обозначение:
Обозначение:
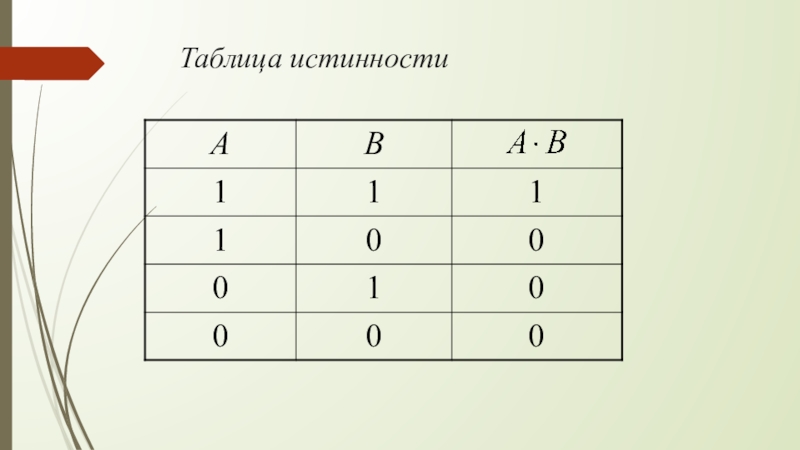
Слайд 5Конъюнкция (логическое умножение)
Конъюнкция двух логических переменных истинна тогда
и только тогда, когда оба высказывания, истинны.
Обозначение:
Обозначение:
Слайд 7 Дизъюнкция (логическое
сложение)
Дизъюнкция двух логических переменных ложна
тогда и только тогда, когда оба высказывания ложны.
Обозначение:
Обозначение:
Слайд 9Импликация (логическое следование)
Импликация двух логических переменных ложна тогда и
только тогда, когда из истинного основания следует ложное следствие.
Обозначение:
А - условие
В - следствие
Обозначение:
А - условие
В - следствие
Слайд 11 Эквивалентность (логическое равенство)
Эквивалентность двух логических переменных истинна
тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Обозначение:
Обозначение:
Слайд 13Приоритет выполнения логических операций
При вычислении значения логического выражения
(формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Пример
1.инверсия,
2.конъюнкция,
3.дизъюнкция,
4.импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Пример
Слайд 14Пример
Дана формула
Определите порядок вычисления.
Порядок вычисления:
Инверсия –
Конъюнкция –
Дизъюнкция –
Импликация
–
Эквивалентность –
Эквивалентность –