- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Повторение_10 класс_Информатика
Содержание
- 1. Презентация по теме Повторение_10 класс_Информатика
- 2. Часть 1.
- 3. B6-1: Выполнение и анализ простых алгоритмовЧто нужно
- 4. Задача №1. На вход алгоритма подаётся натуральное
- 5. Задача №2. На вход алгоритма подаётся натуральное
- 6. Задача №3.Вход: натуральное число N. В конец
- 7. B6-2: Поиск алгоритма минимальной длины для исполнителя.Задача
- 8. B8: Анализ программ с цикламиЧто нужно знать:формулу
- 9. Задача №5. При каком наибольшем введенном числе
- 10. Задача №6. Запишите число, которое будет напечатано
- 11. B11: Рекурсивные алгоритмыЧто нужно знать:рекурсия – это
- 12. Задача №7. Ниже записаны две рекурсивные процедуры:
- 13. Задача №8. Дан рекурсивный алгоритм:function F(n: integer):
- 14. Задача №9. Дан рекурсивный алгоритм:procedure F(n: integer);begin
- 15. B14: Выполнение алгоритмов для исполнителя1. ЧертёжникЗадача №10.
- 16. Задача №10. Чертёжнику был дан для исполнения
- 17. Задача №11. Чертёжнику был дан для исполнения
- 18. 2. РедакторЗадача №12. Редактор получает на вход
- 19. Задача №12. Дана программа для исполнителя Редактор:НАЧАЛОПОКА
- 20. Задача №12. Дана программа для исполнителя Редактор:НАЧАЛОПОКА
- 21. Задача №13. Дана программа для исполнителя Редактор:НАЧАЛОПОКА
- 22. 3. РоботЗадача №14. Система команд исполнителя РОБОТ,
- 23. Задача №14. Сколько клеток лабиринта соответствуют требованию,
- 24. «Двигаться вправо до упора»«Двигаться вниз до упора»Программу
- 25. B19: Обработка массивовЧто нужно знать:работу цикла for
- 26. Задача №16. Массив с индексами от 0
- 27. Задача №17. Массив с индексами от 0
- 28. Задача №18. Массив с индексами от 0
- 29. Задача №19. Массив с индексами от 0
- 30. B20: Циклы и условия («узнай алгоритм»)Задача №20.
- 31. Задача №21. Укажите наименьшее число x, большее
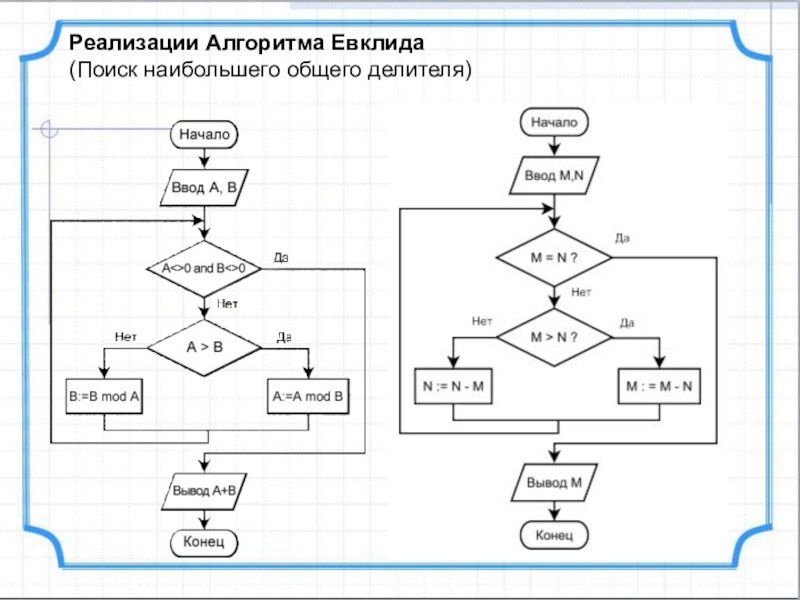
- 32. Реализации Алгоритма Евклида(Поиск наибольшего общего делителя)
- 33. Часть 2.
- 34. B21: Анализ программы с подпрограммамиЧто нужно знать:функция
- 35. Задача №22. Найдите число различных значений k,
- 36. function f(n: longint): longint;begin f:= n*(n-1)+10end;…readln(k);i:= 0;while
- 37. Задача №23. Найдите наименьшее значение k, при
- 38. B22: Динамическое программированиеЧто нужно знать:динамическое программирование –
- 39. Задача №24. У исполнителя Утроитель две команды,
- 40. C24: Исправление ошибокЗадача №25. Считывается натуральное число
- 41. Задача №26. Нужно написать программу, которая выводит
- 42. C25: Обработка массива Задача №27. Дан целочисленный
- 43. Домашнее задание*Подготовиться к КР«ДЗ_Повторение 10 kl.doc»
Слайд 3B6-1: Выполнение и анализ простых алгоритмов
Что нужно знать:
сумма двух цифр в
могут использоваться цифры восьмеричной и шестнадцатеричной систем счисления
бит чётности – это дополнительный контрольный бит, который добавляется к двоичному коду так, чтобы количество единиц в полученном двоичном коде стало чётным; если в исходном коде уже было чётное количество единиц, дописывается 0, если нечётное – дописывается 1.
при добавлении к двоичной записи числа нуля справа число увеличивается в 2 раза
Слайд 4Задача №1. На вход алгоритма подаётся натуральное число N. Алгоритм строит
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 137. В ответе это число запишите в десятичной системе.
Решение:
К числу 2 раза дописывается бит чётности ⇒ после шага «а» у нас всегда получится чётное число единиц ⇒ после «b» всегда добавится ноль
Должны получить чётное = 138, 140, 142, …
После div 2 должна сохраниться чётность!
138 / 2 = 69 = 10001012 :
– 3 ед., нечётность
140 / 2 = 70 = 10001102 :
– 3 ед., нечётность
142 / 2 = 71 = 10001112 :
– 4 ед., чётность
100011
Ответ: 35
Слайд 5Задача №2. На вход алгоритма подаётся натуральное число N. Алгоритм строит
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, которое превышает 43 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.
Решение:
К числу 2 раза дописывается бит чётности ⇒ после шага «а» у нас всегда получится чётное число единиц ⇒ после «b» всегда добавится ноль
min чётное > 43 = 44, 46, 48, …
После div 2 должна сохраниться чётность!
44 / 2 = 22 = 101102 :
– 3 ед., нечётность
46 / 2 = 23 = 101112 :
– 4 ед., чётность
Ответ: 46
Слайд 6
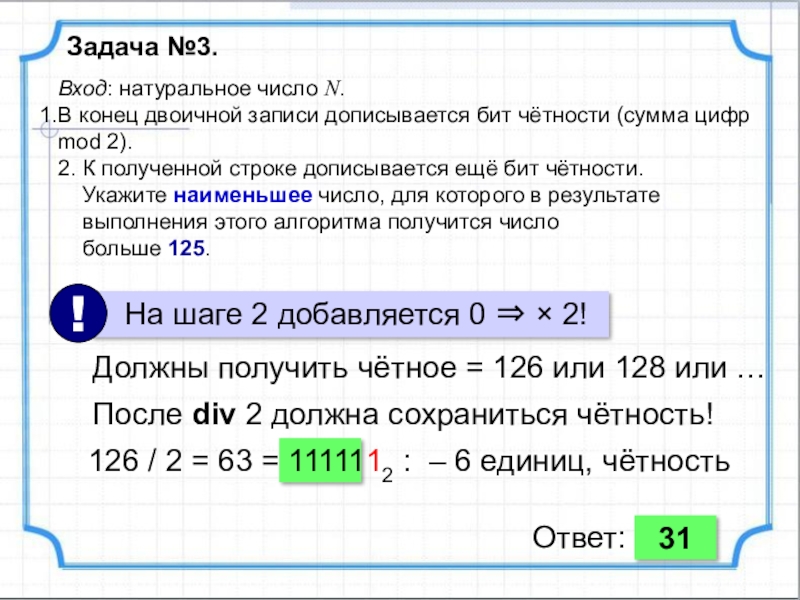
Задача №3.
Вход: натуральное число N.
В конец двоичной записи дописывается бит
2. К полученной строке дописывается ещё бит чётности.
Укажите наименьшее число, для которого в результате
выполнения этого алгоритма получится число больше 125.
Должны получить чётное = 126 или 128 или …
После div 2 должна сохраниться чётность!
126 / 2 = 63 = 1111112 : – 6 единиц, чётность
Слайд 7B6-2: Поиск алгоритма минимальной длины для исполнителя.
Задача №4.
У исполнителя Аккорд
1. отними 1
2. умножь на x
где x – неизвестное положительное число. Выполняя первую из них, Аккорд отнимает от числа на экране 1, а выполняя вторую, умножает это число на x.
Программа для исполнителя Аккорд – это последовательность номеров команд.
Известно, что программа 12121 переводит число 4 в число 23. Определите значение x.
Вход: 4
1: 4 – 1 = 3
2: 3·x = 3x
1: 3·x – 1
2: (3·x – 1) ·x = 3x2– x
1: 3x2– x – 1 = 23
Корни: x1= 3 и x2= – 2,666
Ответ: 3
Слайд 8B8: Анализ программ с циклами
Что нужно знать:
формулу для вычисления n-ого элемента
формулу для вычисления суммы n первых членов арифметической прогрессии:
Слайд 9Задача №5. При каком наибольшем введенном числе d после выполнения программы
var n, s, d: integer;
begin
readln(d);
n := 0;
s := 0;
while s <= 365 do begin
s := s + d;
n := n + 5
end;
write(n)
end.
Начальные значения переменных s и n равны нулю
Шаг изменения переменных
n = 55 ⇒ цикл выполнится 11 раз
s увеличится на d 11 раз и станет равно 0 + 11·d = 11·d
Цикл остановился на 11-м шаге ⇒ 11·d > 365
Цикл не должен остановиться на 10-м шаге ⇒ 10·d ≤ 365
Получаем два неравенства:
n = 55
⇒ d ∈ [34; 36], max = 36
Ответ: 36
Слайд 10Задача №6. Запишите число, которое будет напечатано в результате выполнения программы.
var
begin
s := 33;
n := 1;
while s > 0 do begin
s := s – 7;
n := n * 3
end;
writeln(n)
end.
Начальные значения переменных:
s = 33 и n = 1
Шаг изменения переменных
n увеличивается в 3 раза ⇒ n=3k, где k –число шагов цикла
s уменьшается на 7, конечное значение s = 33 - 7*k ≤ 0, при k=5 (s=33–7*5=-2)
n = 3k = 35 = 243
Ответ: 243
Слайд 11B11: Рекурсивные алгоритмы
Что нужно знать:
рекурсия – это приём, позволяющий свести исходную
чтобы определить рекурсию, нужно задать
условие остановки рекурсии (базовый случай или несколько базовых случаев)
рекуррентную формулу
любую рекурсивную процедуру можно запрограммировать с помощью цикла
Слайд 12Задача №7. Ниже записаны две рекурсивные процедуры: F и G:
procedure F(n:
procedure G(n: integer); forward;
procedure F(n: integer);
begin
if n > 0 then
G(n - 1);
end;
procedure G(n: integer);
begin
writeln('*');
if n > 1 then
F(n - 2);
end;
Сколько символов «звёздочка» будет напечатано на экране при выполнении
вызова F(11)?
Каждая функция вызывает другую (косвенная рекурсия)
Цепочка вызовов:
F(11) → G(10) → F(8) → G(7) → F(5) → G(4) → F(2) → G(1)
За один вызов G выводится одна звёздочка
4 вызова G ⇒ выведено 4 звездочки
Ответ: 4
Слайд 13Задача №8. Дан рекурсивный алгоритм:
function F(n: integer): integer;
begin
if n >
F:= 2*n + F(n-3) + F(n-2)
else
F:= n + 5;
end;
Чему будет равно значение, вычисленное алгоритмом при выполнении вызова F(6)?
4
5
6
13
17
27
40
56
F(2) = 2*2 + 4 + 5 = 13
F(3) = 2*3 + 5 + 6 = 17
Ответ: 56
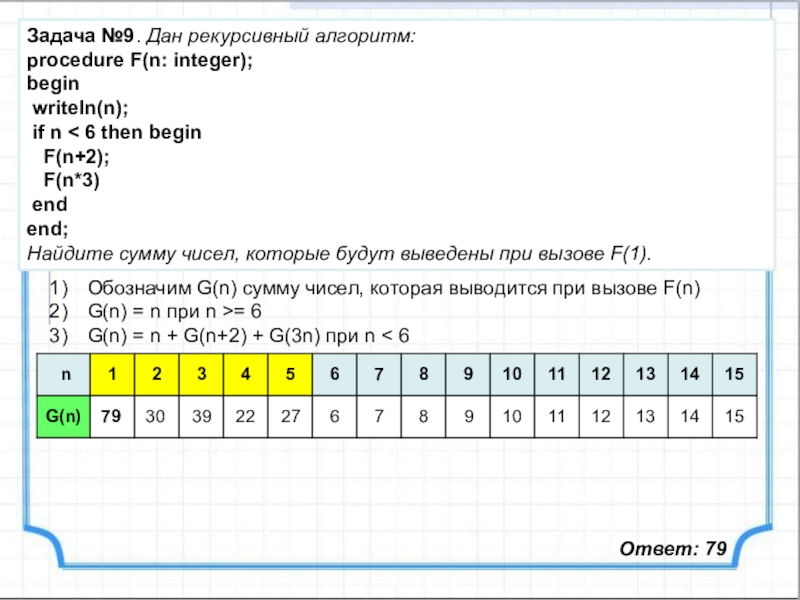
Слайд 14Задача №9. Дан рекурсивный алгоритм:
procedure F(n: integer);
begin
writeln(n);
if n
F(n+2);
F(n*3)
end
end;
Найдите сумму чисел, которые будут выведены при вызове F(1).
Обозначим G(n) сумму чисел, которая выводится при вызове F(n)
G(n) = n при n >= 6
G(n) = n + G(n+2) + G(3n) при n < 6
6
7
8
9
10
11
12
13
14
15
79
30
39
22
27
Ответ: 79
Слайд 15B14: Выполнение алгоритмов для исполнителя
1. Чертёжник
Задача №10.
Исполнитель Чертёжник перемещается на
Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Слайд 16Задача №10. Чертёжнику был дан для исполнения следующий алгоритм (буквами n,
НАЧАЛО
сместиться на (–1, –2)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (-1, -2)
КОНЕЦ ПОВТОРИ
сместиться на (–24, -12)
КОНЕЦ
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
Общее изменение координат:
Чертёжник должен вернуться в исходную точку ⇒ эти величины должны быть равны нулю
Найти max n∈N, при котором система уравнений разрешима в целых числах относительно a и b
N = НОД (25,14)
Ответ: 1
Слайд 17Задача №11. Чертёжнику был дан для исполнения следующий алгоритм (буквами n,
НАЧАЛО
сместиться на (–3, –3)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (27, 12)
КОНЕЦ ПОВТОРИ
сместиться на (–22, -7)
КОНЕЦ
Укажите наименьшее возможное значение числа n (n > 1), для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
Общее изменение координат:
Чертёжник должен вернуться в исходную точку ⇒ эти величины должны быть равны нулю
N = наименьший общий делитель (25,10) >1
Ответ: 5
Слайд 182. Редактор
Задача №12.
Редактор получает на вход строку цифр и преобразовывает
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
заменить (v, w)
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w.
нашлось (v)
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка при этом не изменяется.
Слайд 19Задача №12.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось
ЕСЛИ нашлось (222)
ТО заменить (222, 5)
ИНАЧЕ заменить (555, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, состоящей из
А) 247 идущих подряд цифр 5?
Б) 247 идущих подряд цифр 2?
В ответе запишите полученную строку.
А
Как поступить, если остаток от деления равен 0?
Например, будут даны двадцать четыре «5».
Тогда выполним шаг назад, когда оставались последние восемь «5»: 55555555 → 255555 → 2255
555555555…5
247
555555555…5
9 «5» заменяются на одну «5» ⇒ при каждом повторении действий вычеркиваются по восемь «5»
Сколько «5» остались не вычеркнутыми?
Вычислим целочисленный остаток:
247 mod 8 = 7
5555555
225
Ответ: 225
Слайд 20Задача №12.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось
ЕСЛИ нашлось (222)
ТО заменить (222, 5)
ИНАЧЕ заменить (555, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, состоящей из
А) 247 идущих подряд цифр 5?
Б) 247 идущих подряд цифр 2?
В ответе запишите полученную строку.
Б
222222222…2
247
222222222…2
Теперь к последовательности применим алгоритм, описанный в пункте А.
82 mod 8 = 2
Не происходит замена трех «5» на «2»!
Происходит замена следующих трех «2» на «5»
247 div 3 = 82
247 mod 3 = 1
555555555…52
82
552
Ответ: 552
Слайд 21Задача №13.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось
ЕСЛИ нашлось (222)
ТО заменить (222, 8)
ИНАЧЕ заменить (888, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 68 идущих подряд цифр 8?
В ответе запишите полученную строку.
888888888…8
68
888888888…8
9 «8» заменяются на одну «8» ⇒ при каждом повторении действий вычеркиваются по восемь «8»
68 mod 8 = 4
8888
28
Ответ: 28
Слайд 223. Робот
Задача №14.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте
вверх вниз влево вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
сверху свободно, снизу свободно, слева свободно, справа свободно
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если
условие ложно).
Если РОБОТ начнёт движение в сторону находящейся рядом с ним
стены, то он разрушится и программа прервётся.
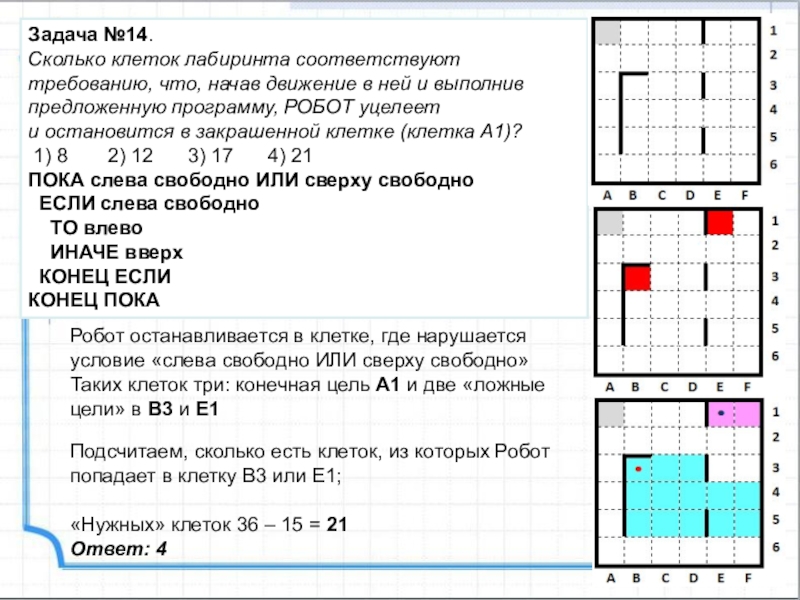
Слайд 23Задача №14.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в
и остановится в закрашенной клетке (клетка А1)?
1) 8 2) 12 3) 17 4) 21
ПОКА слева свободно ИЛИ сверху свободно
ЕСЛИ слева свободно
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
Робот останавливается в клетке, где нарушается условие «слева свободно ИЛИ сверху свободно»
Таких клеток три: конечная цель А1 и две «ложные цели» в В3 и Е1
Подсчитаем, сколько есть клеток, из которых Робот попадает в клетку В3 или E1;
«Нужных» клеток 36 – 15 = 21
Ответ: 4
Слайд 24«Двигаться вправо до упора»
«Двигаться вниз до упора»
Программу можно записать в свободном
ПОКА не пришли в угол
двигаться вправо до упора
двигаться вниз до упора
КОНЕЦ ПОКА
где угол – есть стенки снизу и справа
Один шаг внешнего цикла
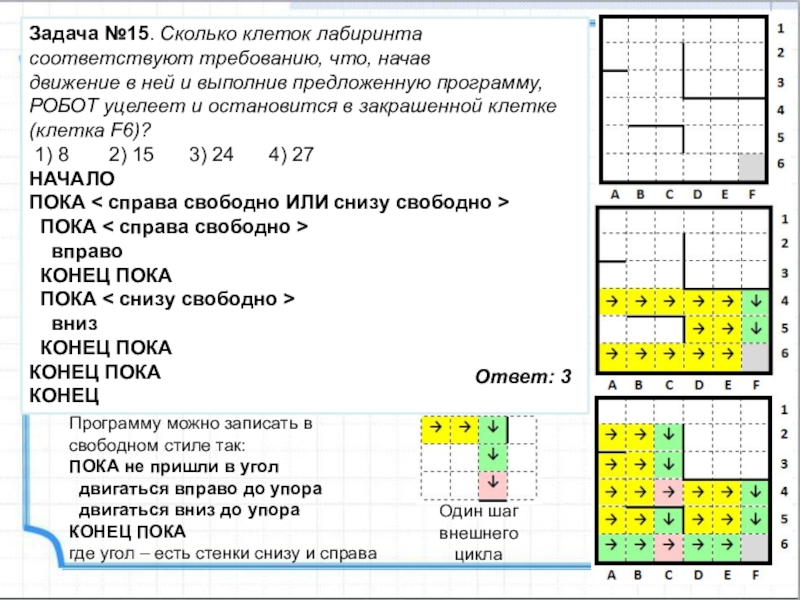
Задача №15. Сколько клеток лабиринта соответствуют требованию, что, начав
движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
1) 8 2) 15 3) 24 4) 27
НАЧАЛО
ПОКА < справа свободно ИЛИ снизу свободно >
ПОКА < справа свободно >
вправо
КОНЕЦ ПОКА
ПОКА < снизу свободно >
вниз
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
Ответ: 3
Слайд 25B19: Обработка массивов
Что нужно знать:
работу цикла for (цикла с переменной)
массив –
для обращения к элементу массива используют квадратные скобки, запись A[i] обозначает элемент массива A с номером (индексом) i
матрица (двухмерный массив) – это прямоугольная таблица однотипных элементов
если матрица имеет имя A, то обращение A[i,k] обозначает элемент, расположенный на пересечении строки i и столбца k
Слайд 26Задача №16.
Массив с индексами от 0 до 9.
for i:= 1 to 9 do
if A[i-1] < A[i] then begin
c:= c + 1;
t:= A[i];
A[i]:= A[i-1];
A[i-1]:= t
end;
Какое значение будет иметь переменная «c»?
перестановка пары при сортировке пузырьком
6 9 7 2 1 5 0 3 4 8
1) 9 6 7 2 1 5 0 3 4 8
2) 9 7 6 2 1 5 0 3 4 8
3) 9 7 6 2 5 1 0 3 4 8
4) 9 7 6 2 5 1 3 0 4 8
5) 9 7 6 2 5 1 3 4 0 8
6) 9 7 6 2 5 1 3 4 8 0
с = 6
Исходный массив:
6 9 7 2 1 5 0 3 4 8
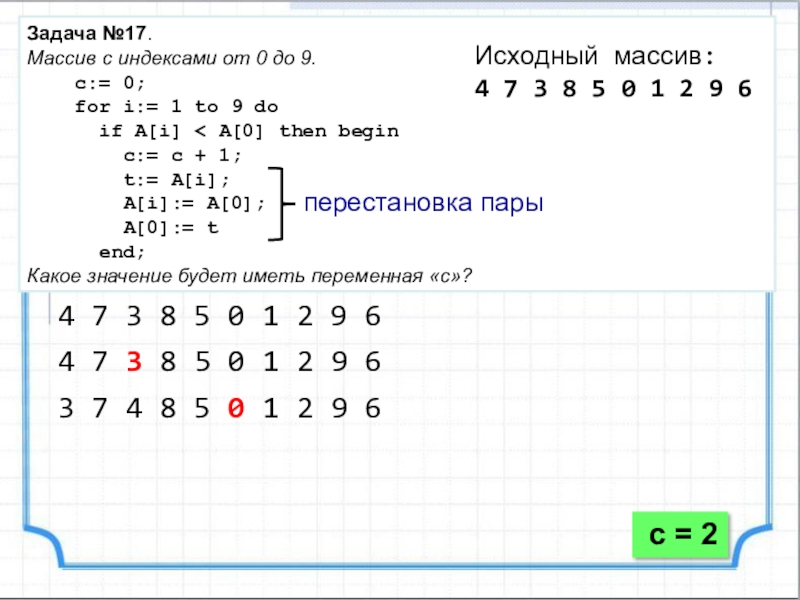
Слайд 27Задача №17.
Массив с индексами от 0 до 9.
for i:= 1 to 9 do
if A[i] < A[0] then begin
c:= c + 1;
t:= A[i];
A[i]:= A[0];
A[0]:= t
end;
Какое значение будет иметь переменная «c»?
перестановка пары
4 7 3 8 5 0 1 2 9 6
4 7 3 8 5 0 1 2 9 6
3 7 4 8 5 0 1 2 9 6
с = 2
Исходный массив:
4 7 3 8 5 0 1 2 9 6
Слайд 28
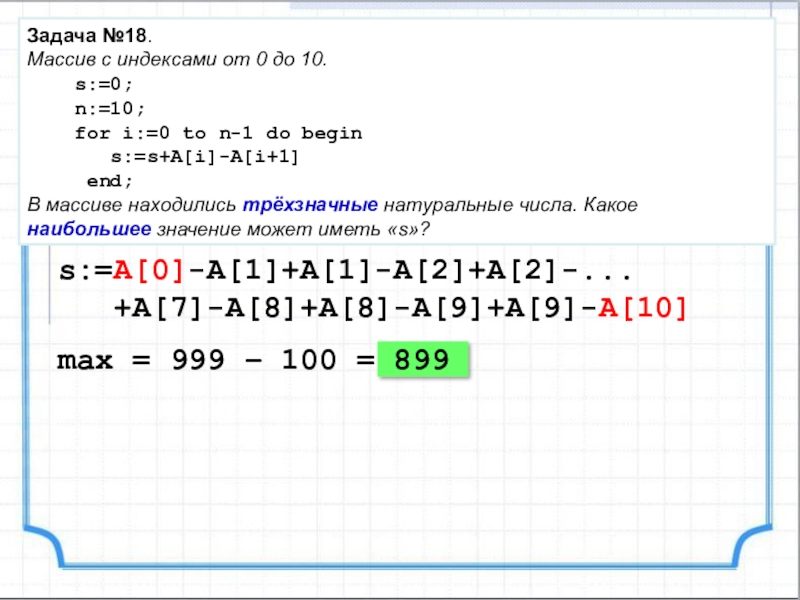
Задача №18.
Массив с индексами от 0 до 10.
n:=10;
for i:=0 to n-1 do begin
s:=s+A[i]-A[i+1]
end;
В массиве находились трёхзначные натуральные числа. Какое наибольшее значение может иметь «s»?
s:=A[0]-A[1]+A[1]-A[2]+A[2]-...
+A[7]-A[8]+A[8]-A[9]+A[9]-A[10]
max = 999 – 100 = 899
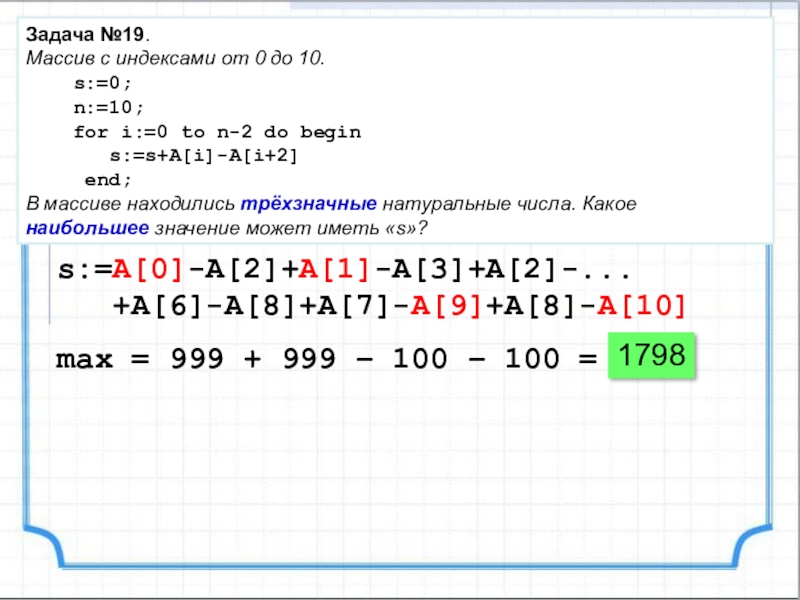
Слайд 29Задача №19.
Массив с индексами от 0 до 10.
n:=10;
for i:=0 to n-2 do begin
s:=s+A[i]-A[i+2]
end;
В массиве находились трёхзначные натуральные числа. Какое наибольшее значение может иметь «s»?
s:=A[0]-A[2]+A[1]-A[3]+A[2]-...
+A[6]-A[8]+A[7]-A[9]+A[8]-A[10]
max = 999 + 999 – 100 – 100 = 1798
1798
Слайд 30B20: Циклы и условия («узнай алгоритм»)
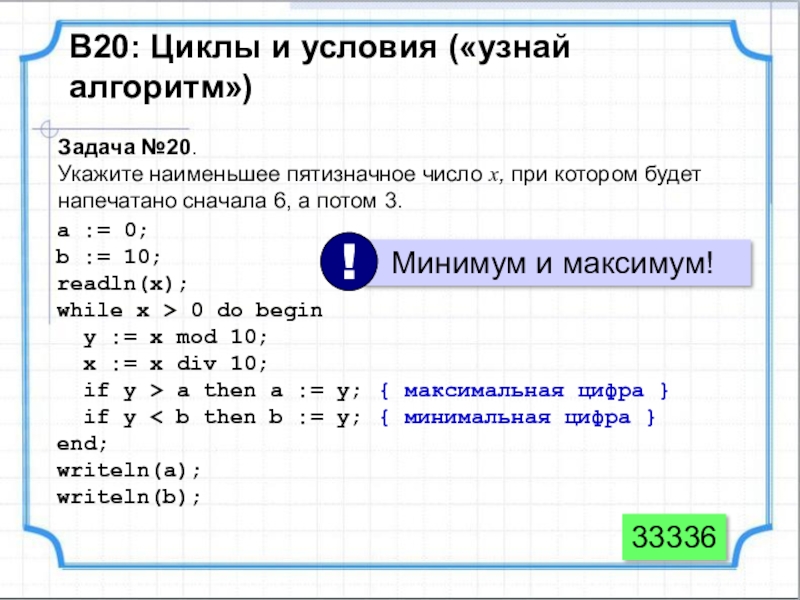
Задача №20.
Укажите наименьшее пятизначное число
a := 0;
b := 10;
readln(x);
while x > 0 do begin
y := x mod 10;
x := x div 10;
if y > a then a := y;
if y < b then b := y;
end;
writeln(a);
writeln(b);
33336
{ максимальная цифра }
{ минимальная цифра }
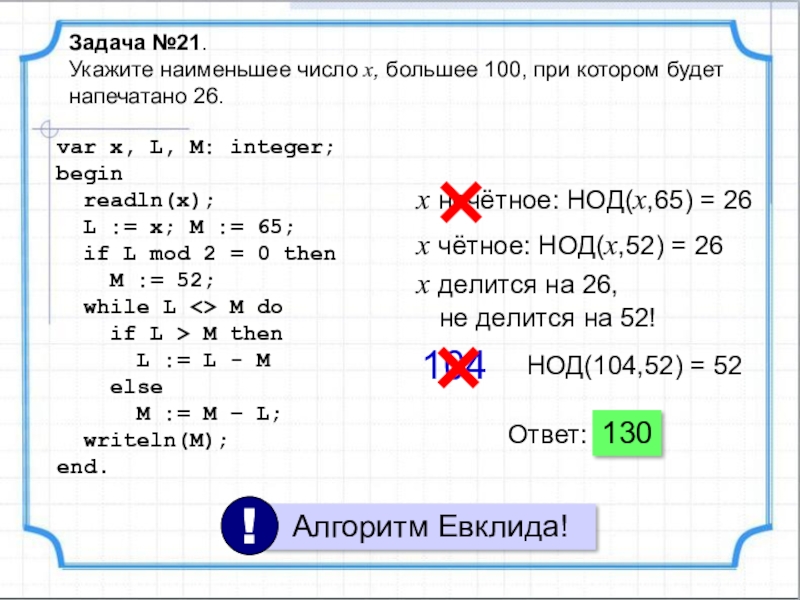
Слайд 31Задача №21.
Укажите наименьшее число x, большее 100, при котором будет
var x, L, M: integer;
begin
readln(x);
L := x; M := 65;
if L mod 2 = 0 then
M := 52;
while L <> M do
if L > M then
L := L - M
else
M := M – L;
writeln(M);
end.
x нечётное: НОД(x,65) = 26
x чётное: НОД(x,52) = 26
x делится на 26,
не делится на 52!
104
НОД(104,52) = 52
Слайд 34B21: Анализ программы с подпрограммами
Что нужно знать:
функция – это вспомогательный алгоритм,
оформляется следующим образом (вместо многоточия могут быть любые операторы):
function F(x: integer):integer;
begin
...
F:= <результат функции>
end;
в заголовке функции записывают имя функции, в скобках – список параметров, далее через двоеточие – тип возвращаемого значения; в приведенном примере функция F принимает один целый параметр, к которому внутри функции нужно обращаться по имени x, и возвращает целое число
результат функции записывается в специальную переменную, имя которой совпадает с именем функции; объявлять эту переменную не нужно
Слайд 35Задача №22.
Найдите число различных значений k, при которых программа выдаёт
function f(n: longint): longint;
begin
f:= n*(n-1)+10
end;
…
readln(k);
i:= 0;
while f(i) < k do
i:= i + 1;
writeln(i);
36
Останов: k <= f(i)
31 … 40
10
8
23 … 30
Слайд 36
function f(n: longint): longint;
begin
f:= n*(n-1)+10
end;
…
readln(k);
i:= 0;
while f(i) < k do
writeln(i);
Останов:
f(i-1) < k <= f(i)
31 … 40
(i-1)*(i-2)+10 < k <= i*(i-1)+10
i2-3i+12 < k <= i2-i+10
i=6: 30 < k <= 40
Задача №22.
Найдите число различных значений k, при которых программа выдаёт тот же ответ, что и при k = 36.
Слайд 37Задача №23.
Найдите наименьшее значение k, при котором программа выдаёт тот
var k, i : longint;
function f(n: longint): longint;
begin f := n * n * n;
end;
function g(n: longint): longint;
begin g := 2*n + 3;
end;
begin
readln(k);
i := 1;
while f(i) < g(k) do
i := i+1;
writeln(i)
end.
Останов:
f(i-1) < g(k) <= f(i)
3 … 12
(i-1)3 < 2k+3 <= i3
k=10: (i-1)3 < 23 <= i3
i=3
8 < 2k+3 <= 27
Слайд 38B22: Динамическое программирование
Что нужно знать:
динамическое программирование – это способ решения сложных
с помощью динамического программирования решаются задачи, которые требуют полного перебор вариантов:
«подсчитайте количество вариантов…»
«как оптимально распределить…»
«найдите оптимальный маршрут…»
динамическое программирование позволяет ускорить выполнение программы за счет использования дополнительной памяти; полный перебор не требуется, поскольку запоминаются решения всех задач с меньшими значениями параметров
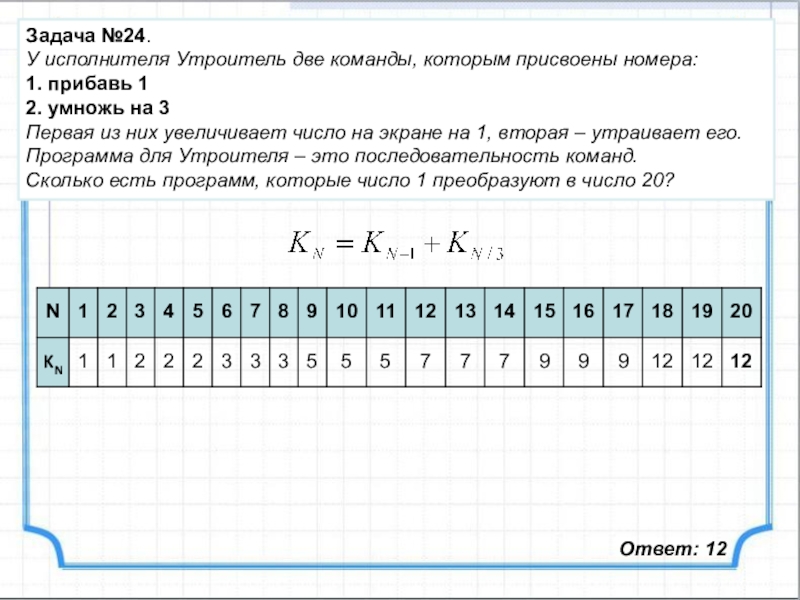
Слайд 39Задача №24.
У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь
2. умножь на 3
Первая из них увеличивает число на экране на 1, вторая – утраивает его.
Программа для Утроителя – это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в число 20?
Ответ: 12
Слайд 40C24: Исправление ошибок
Задача №25.
Считывается натуральное число x, нужно найти количество
…
readln(x);
c:= 0;
while x > 0 do begin
c:= c + x mod 2;
x:= x div 10
end;
writeln(c)
…
ЗАДАНИЕ
Что выведет эта программа при вводе числа 15.
Приведите пример такого числа x, что, несмотря на ошибки, программа печатает правильный ответ.
Найдите все ошибки в этой программе.
Для каждой ошибки:
выпишите строку, в которой сделана ошибка;
укажите, как исправить ошибку.
Возможные ошибки
неверное начальное значение
неверное условие цикла
неверное изменение переменных
неверный вывод
Решение:
2
x = 1
1-я ошибка (знач. нули)
c:= c + x mod 2;
c:= c + 1;
2-я ошибка (обработка x)
x:= x div 10
x:= x div 2
Слайд 41Задача №26.
Нужно написать программу, которая выводит на экран максимальную цифру
readln(N);
maxDigit := N mod 10;
while N > 0 do begin
digit := N mod 10;
if digit mod 3 = 0 then
if digit > maxDigit then
maxDigit := digit;
N := N div 10;
end;
if maxDigit = 0 then
writeln('NO')
else
writeln(maxDigit);
ЗАДАНИЕ
Напишите, что выведет эта программа при вводе числа 134.
Приведите пример такого трёхзначного числа, при вводе которого программа выдаёт верный ответ.
Найдите все ошибки в этой программе.
Для каждой ошибки:
выпишите строку, в которой сделана ошибка;
укажите, как исправить ошибку.
Решение:
4
333
1-я ошибка (Иниц-ия maxDigit)
maxDigit := N mod 10;
maxDigit := -1; {< 0}
2-я ошибка (Условие вывода)
if maxDigit = 0 then
if maxDigit = -1 then
Когда работает верное
последняя цифра делится на 3
последняя цифра меньше, чем нужный результат
Слайд 42C25: Обработка массива
Задача №27.
Дан целочисленный массив из 40 элементов.
const
N=40;
var a: array [1..N] of integer;
i, j, k: longint;
begin
for i:=1 to N do
readln(a[i]);
…
end.
k := 0;
for i := 1 to N-1 do
if ((a[i]+a[i+1]) mod 6 <> 0) and
(a[i]*a[i+1] < 1000) then
k := k + 1;
writeln(k);