Урок №1
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Основы логики 1, 2 уроки
Содержание
- 1. Презентация по теме Основы логики 1, 2 уроки
- 2. ЛОГИКАНАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ
- 3. МЫШЛЕНИЕ ОСУЩЕСТВЛЯЕТСЯ ЧЕРЕЗ: Понятия Высказывания Умозаключения
- 4. ПОНЯТИЕ форма мышления, которая выделяет существенные признаки
- 5. ВЫСКАЗЫВАНИЕформулировка своего понимания окружающего мира (повествовательное предложение
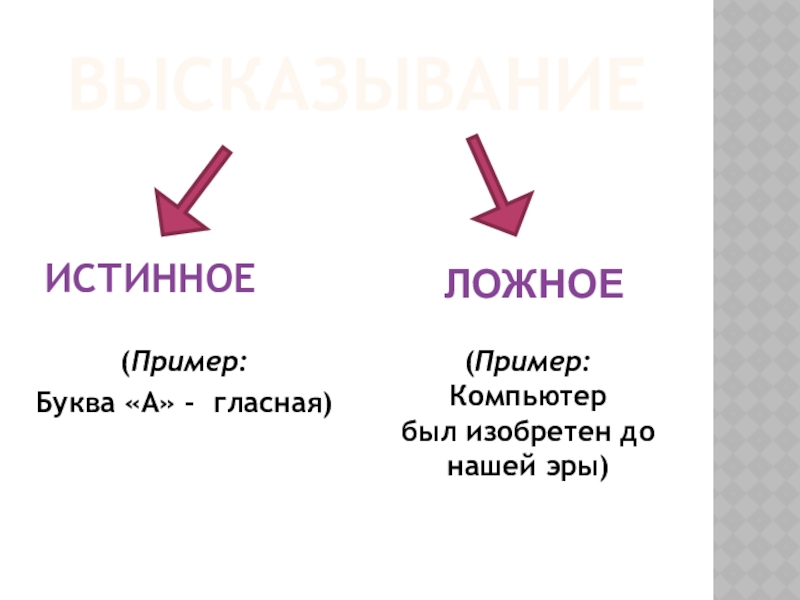
- 6. ВЫСКАЗЫВАНИЕИСТИННОЕ (Пример: Буква «А» - гласная) ЛОЖНОЕ(Пример: Компьютербыл изобретен до нашей эры)
- 7. УМОЗАКЛЮЧЕНИЕформа мышления, с помощью которой из одного
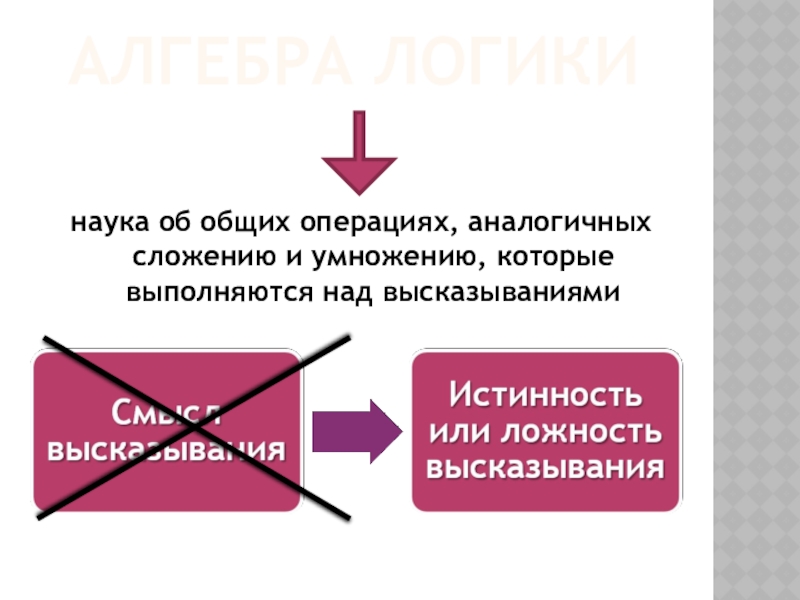
- 8. АЛГЕБРА ЛОГИКИнаука об общих операциях, аналогичных сложению и умножению, которые выполняются над высказываниями
- 9. ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ:Логическая переменная – это простое
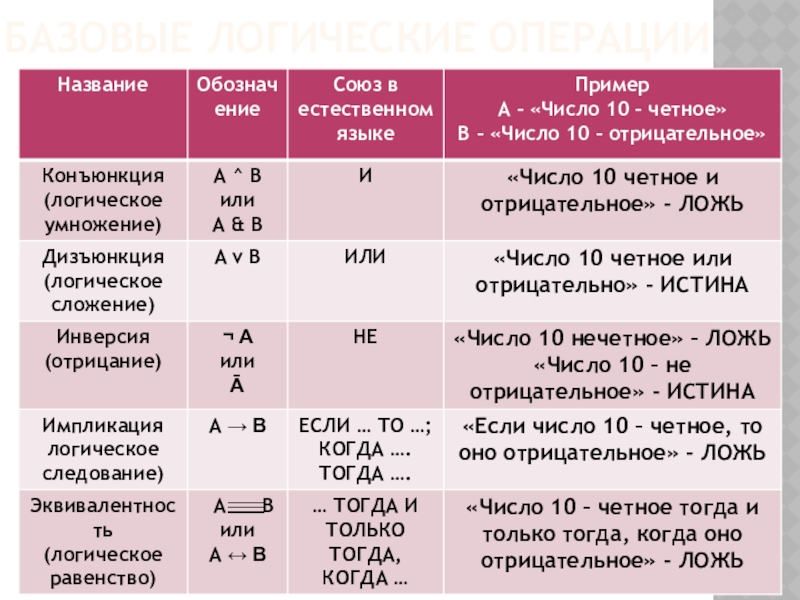
- 10. БАЗОВЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- 11. ТАБЛИЦА ИСТИННОСТИтаблица определяющая значение сложного высказывания при всех возможных значениях простых высказываний
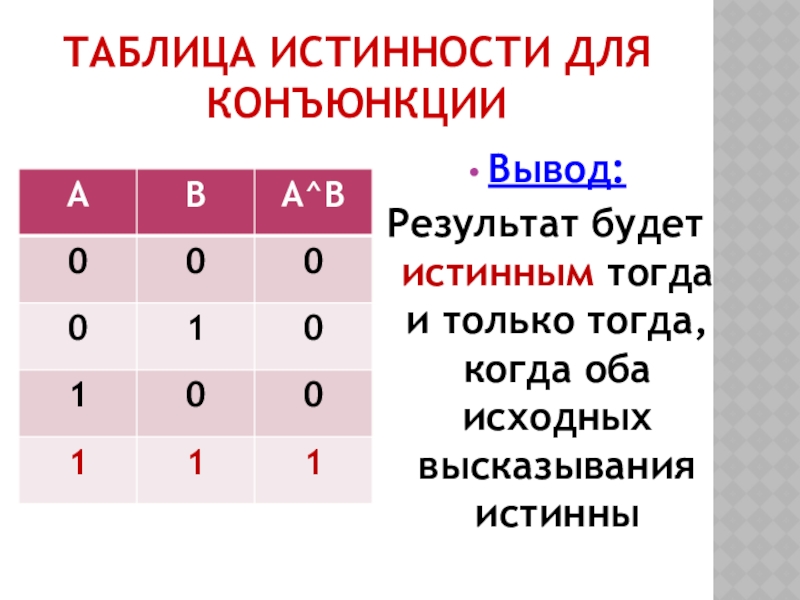
- 12. ТАБЛИЦА ИСТИННОСТИ ДЛЯ КОНЪЮНКЦИИВывод: Результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны
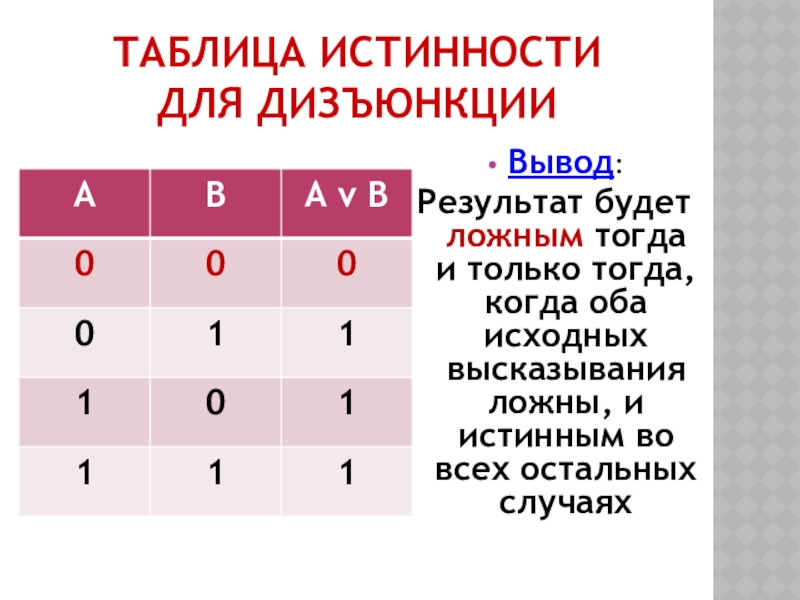
- 13. ТАБЛИЦА ИСТИННОСТИ ДЛЯ ДИЗЪЮНКЦИИВывод: Результат будет
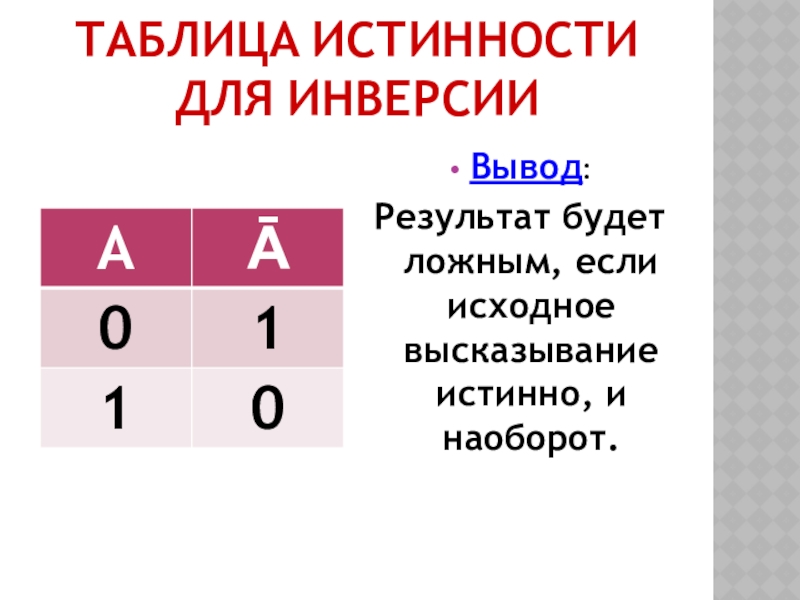
- 14. ТАБЛИЦА ИСТИННОСТИ ДЛЯ ИНВЕРСИИВывод: Результат будет ложным, если исходное высказывание истинно, и наоборот.
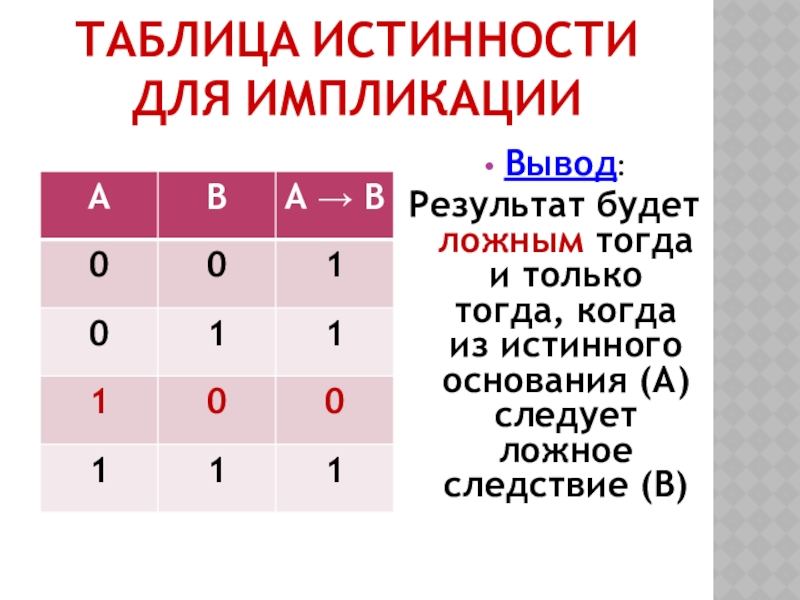
- 15. ТАБЛИЦА ИСТИННОСТИ ДЛЯ ИМПЛИКАЦИИВывод: Результат будет ложным
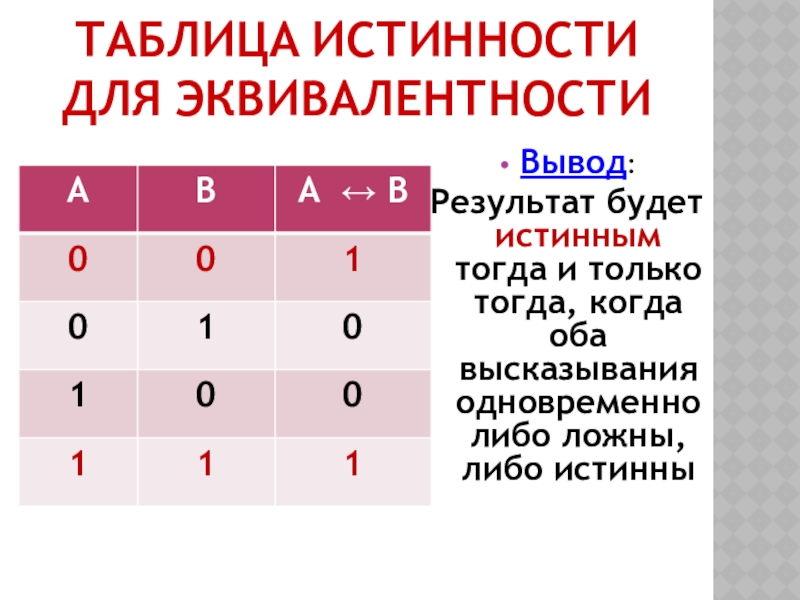
- 16. ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЭКВИВАЛЕНТНОСТИВывод: Результат будет истинным
- 17. Если составное высказывание (логическую функцию) выразить в
- 18. ПОРЯДОК ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ: Действия в скобках Инверсия Конъюнкция Дизъюнкция Импликация Эквивалентность
- 19. ПРИМЕР: ЗАПИСАТЬ В ВИДЕ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ СЛЕДУЮЩЕЕ
- 20. УПРАЖНЕНИЯ:Есть два простых высказывания:А = «Число 10
- 21. ОСНОВЫ ЛОГИКИУрок №2
- 22. УПРАЖНЕНИЯ:3. Решить логические выражения:F(A, B) =¬(А v
- 23. 3. Решить логические выражения:1) F(A, B) =¬(А v В)^( A ^ ¬B)
- 24. 3. Решить логические выражения:2) F(A, B, C) =C v ( B ^ A ^ ¬C)
- 25. 3. Решить логические выражения:3) F(A, B, C) =А ^ В v ¬B v ¬A ^ C
- 26. 3. Решить логические выражения:4) F(A, B, C)
- 27. 3. Решить логические выражения:5) F(A, B, C) = (A v B) → (¬A v C)
- 28. 3. Решить логические выражения:6) F(A, B, C) = ¬A v С v (A ^ ¬B)
- 29. 3. Решить логические выражения:7) F(A, B, C) = (A v B) ^ (¬A v C)
- 30. 3. Решить логические выражения:8) F(A, B, C)
- 31. 3. Решить логические выражения:9) F(A, B, C) = (A ^ B) → (A v ¬C)
ЛОГИКАНАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ
Слайд 1ОСНОВЫ ЛОГИКИ
Муравьева Инна Владимировна
Учитель информатики и ИКТ
МБОУ «Гимназия №11»
г. Выборг, Ленинградская
обл.
Слайд 4ПОНЯТИЕ
форма мышления, которая выделяет существенные признаки предмета или класса предметов,
позволяющие отличать их друг от друга
(Пример: Прямоугольник - геометрическая фигура у которой все углы прямые и противоположные стороны равны)
(Пример: Прямоугольник - геометрическая фигура у которой все углы прямые и противоположные стороны равны)
Слайд 5ВЫСКАЗЫВАНИЕ
формулировка своего понимания окружающего мира (повествовательное предложение в котором что-либо утверждается
или отрицается)
(Пример: Париж – столица Франции)
(Пример: Париж – столица Франции)
Слайд 6ВЫСКАЗЫВАНИЕ
ИСТИННОЕ
(Пример:
Буква «А» - гласная)
ЛОЖНОЕ
(Пример:
Компьютер
был изобретен до нашей эры)
Слайд 7УМОЗАКЛЮЧЕНИЕ
форма мышления, с помощью которой из одного или нескольких суждений может
быть получено новое суждение
(знание или вывод)
(Пример: любая теорема)
(знание или вывод)
(Пример: любая теорема)
Слайд 8АЛГЕБРА ЛОГИКИ
наука об общих операциях, аналогичных сложению и умножению, которые выполняются
над высказываниями
Слайд 9ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ:
Логическая переменная – это простое высказывание, содержащее только одну
мысль
Обозначение: латинская буква (А, В, Х …)
Значение: ИСТИНА (1) или ЛОЖЬ (0)
Логическая функция – это составное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций
Обозначение: F
Логические операции – логическое действие
Обозначение: латинская буква (А, В, Х …)
Значение: ИСТИНА (1) или ЛОЖЬ (0)
Логическая функция – это составное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций
Обозначение: F
Логические операции – логическое действие
Слайд 11ТАБЛИЦА ИСТИННОСТИ
таблица определяющая значение сложного высказывания при всех возможных значениях простых
высказываний
Слайд 12ТАБЛИЦА ИСТИННОСТИ ДЛЯ КОНЪЮНКЦИИ
Вывод:
Результат будет истинным тогда и только тогда,
когда оба исходных высказывания истинны
Слайд 13ТАБЛИЦА ИСТИННОСТИ
ДЛЯ ДИЗЪЮНКЦИИ
Вывод:
Результат будет ложным тогда и только тогда,
когда оба исходных высказывания ложны, и истинным во всех остальных случаях
Слайд 14ТАБЛИЦА ИСТИННОСТИ ДЛЯ ИНВЕРСИИ
Вывод:
Результат будет ложным, если исходное высказывание истинно,
и наоборот.
Слайд 15ТАБЛИЦА ИСТИННОСТИ ДЛЯ ИМПЛИКАЦИИ
Вывод:
Результат будет ложным тогда и только тогда,
когда из истинного основания (А) следует ложное следствие (В)
Слайд 16ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЭКВИВАЛЕНТНОСТИ
Вывод:
Результат будет истинным тогда и только тогда,
когда оба высказывания одновременно либо ложны, либо истинны
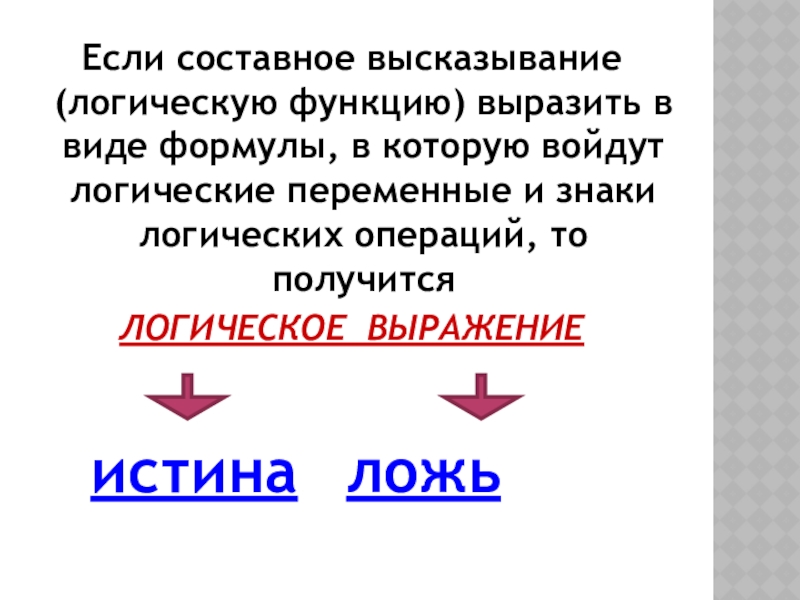
Слайд 17Если составное высказывание (логическую функцию) выразить в виде формулы, в которую
войдут логические переменные и знаки логических операций, то получится
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
истина ложь
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
истина ложь
Слайд 18ПОРЯДОК ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ:
Действия в скобках
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность
Эквивалентность
Слайд 19ПРИМЕР: ЗАПИСАТЬ В ВИДЕ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ СЛЕДУЮЩЕЕ ВЫСКАЗЫВАНИЕ: «ЛЕТОМ ПЕТЯ ПОЕДЕТ
В ДЕРЕВНЮ И, ЕСЛИ БУДЕТ ХОРОШАЯ ПОГОДА, ТО ОН ПОЙДЕТ НА РЫБАЛКУ»
Это составное высказывание состоит из простых высказываний:
А = «Петя поедет в деревню»
В = «Будет хорошая погода»
С = «Он пойдет на рыбалку»
Записываем высказывание в виде логического выражения, учитывая порядок действий
F = A ^ (B → C)
Слайд 20УПРАЖНЕНИЯ:
Есть два простых высказывания:
А = «Число 10 четное»
В = Волк –
травоядное животное»
Составьте из них все возможные составные высказывания и определите их истинность
Запишите следующие высказывания в виде логических выражений:
Неверно, что корова – хищное животное
На уроке физики ученики выполняли лабораторную работу и сообщали результаты учителю.
Если Маша – сестра Саши, то Саша - брат Маши.
Составьте из них все возможные составные высказывания и определите их истинность
Запишите следующие высказывания в виде логических выражений:
Неверно, что корова – хищное животное
На уроке физики ученики выполняли лабораторную работу и сообщали результаты учителю.
Если Маша – сестра Саши, то Саша - брат Маши.
Слайд 22УПРАЖНЕНИЯ:
3. Решить логические выражения:
F(A, B) =¬(А v В)^( A ^ ¬B)
F(A,
B, C) =C v ( B ^ A ^ ¬C)
F(A, B, C) =А ^ В v ¬B v ¬A ^ C
F(A, B, C) =А ^ ¬B ^ C v A v B v ¬C
F(A, B, C) = (A v B) → (¬A v C)
F(A, B, C) = ¬A v С v (A ^ ¬B)
F(A, B, C) = (A v B) ^ (¬A v C)
F(A, B, C) = A ^¬B ^ C v A v B v ¬C
F(A, B, C) = (A ^ B) → (A v ¬C)
F(A, B, C) =А ^ В v ¬B v ¬A ^ C
F(A, B, C) =А ^ ¬B ^ C v A v B v ¬C
F(A, B, C) = (A v B) → (¬A v C)
F(A, B, C) = ¬A v С v (A ^ ¬B)
F(A, B, C) = (A v B) ^ (¬A v C)
F(A, B, C) = A ^¬B ^ C v A v B v ¬C
F(A, B, C) = (A ^ B) → (A v ¬C)
