- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Машина Тьюринга
Содержание
- 1. Презентация по теме Машина Тьюринга
- 2. Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический
- 3. Структура и описание машины Тьюринга
- 4. 1) Внешний алфавит А = {a0, a1, …,
- 5. 2) Внутренний алфавит Q = {q0, q1, …,
- 6. Виды команд машины ТьюрингаНаписать новую букву в
- 7. 3) Внешняя память (лента)Машина имеет ленту, разбитую
- 8. 3) Внешняя память (лента)Устройство машины ТьюрингаПустая клетка
- 9. 4) Каретка (управляющая головка)Каретка машины располагается над
- 10. 5) Функциональная схема (программа)Программа машины состоит из
- 11. К началу работы машины на ленту подается
- 12. Описание работы машины ТьюрингаСтандартное положение называется начальным
- 13. Находясь в не заключительном состоянии, машина совершает
- 14. Описание работы машины ТьюрингаВ соответствии с командой
- 15. При переходе машины в заключительное состояние q0
- 16. Машинным словом (конфигурацией) машины Тьюринга называется слово
- 17. Конфигурация α1qkal α2 интерпретируется следующим образом:- машина
- 18. Ситуации неприменимости машины Тьюринга Считается, что машина Тьюринга
- 19. Пример машин Тьюринга Требуется построить машину Тьюринга для
- 20. Реализуйте предложенный алгоритм Машина Тьюринга прибавляет единицу к
- 21. Реализуйте предложенный алгоритм На ленте машины Тьюринга содержится
- 22. ПримерДана машина Тьюринга с внешним алфавитом А
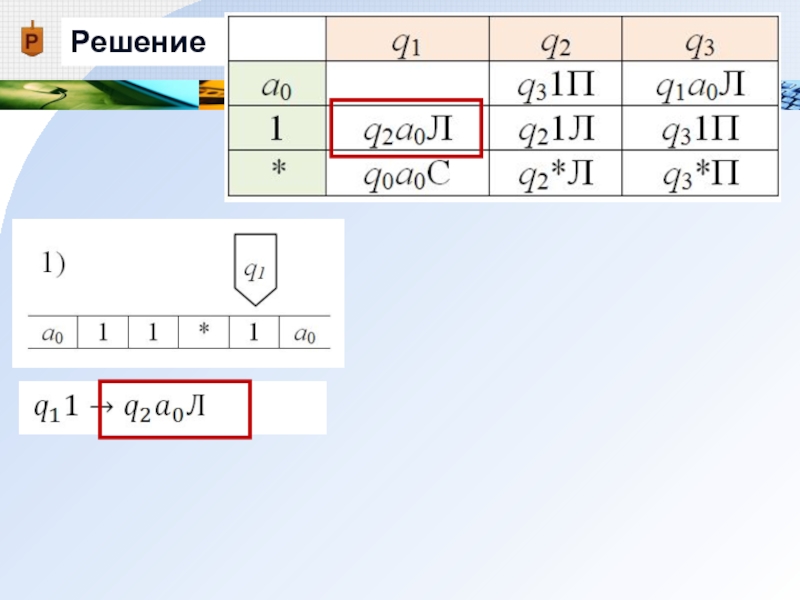
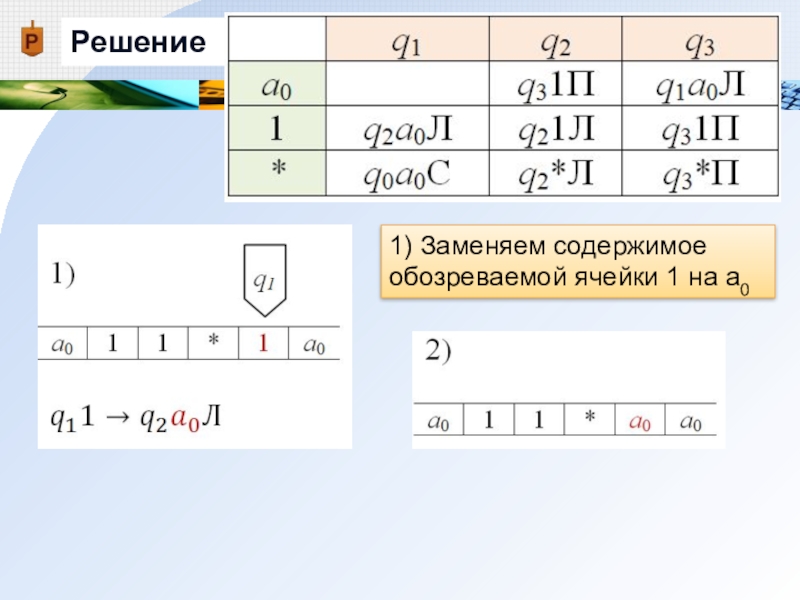
- 23. Решение
- 24. Решение1) Заменяем содержимое обозреваемой ячейки 1 на а0
- 25. Решение2) Машина переходит в новое состояние q2
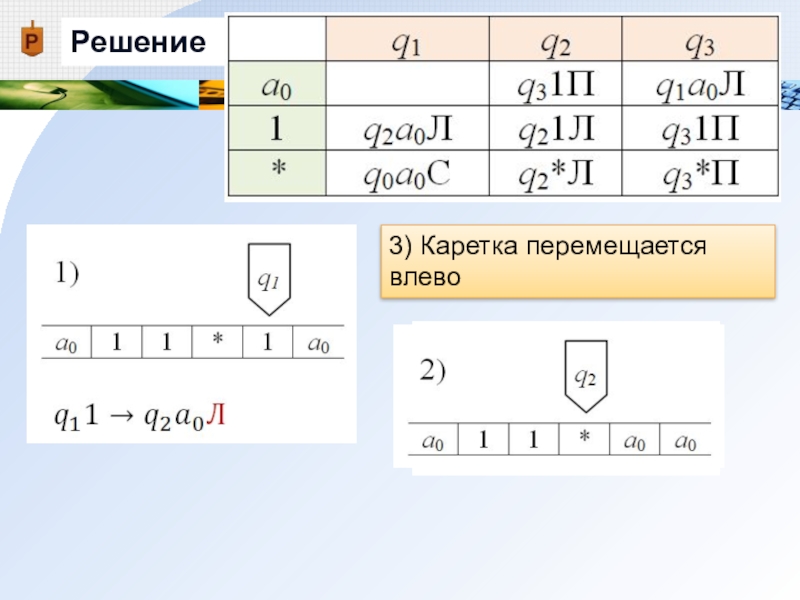
- 26. Решение3) Каретка перемещается влево
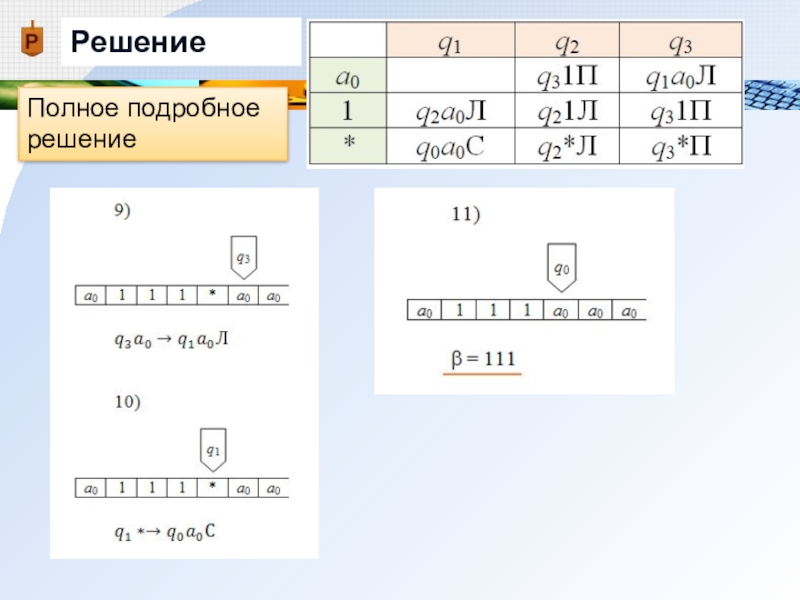
- 27. РешениеПолное подробное решение
- 28. РешениеПолное подробное решение
- 29. РешениеПолное подробное решение
- 30. РешениеРешение, записанное с помощью конфигураций (в строчку)
- 31. α = 1*11Ответ: β = 111
- 32. ЛитератураИгошин В.И. Математическая логика и теория алгоритмов.
- 33. Люди могут вести себя по-разному в одинаковых ситуациях, и этим они принципиально отличаются от машин.
Слайд 2Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс, созданный для уточнения
Это математический объект, а не физическая машина.
Предложена Аланом Тьюрингом в 1936 году
Машина Тьюринга – это строгое математическое построение, математический аппарат, созданный для решения определённых задач.
Слайд 3Структура и описание машины Тьюринга
Машина Тьюринга состоит из:
бесконечной ленты, разделенной на ячейки;
каретки (читающей и записывающей головки);
программируемого автомата (программа в виде таблицы).
Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую букву он видит, а также в зависимости от своего состояния q автомат может выполнять следующие действия:
записать новую букву в обозреваемую ячейку;
выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
перейти в новое состояние.
Слайд 4
1) Внешний алфавит
А = {a0, a1, …, an}
Элемент a0 называется пустой
В этом алфавите в виде слова кодируется исходный набор данных и результат работы алгоритма.
Устройство машины Тьюринга
Слайд 5
2) Внутренний алфавит
Q = {q0, q1, …, qm}, {П, Л, Н!}
В
При этом: q1 - начальное состояние (машина начинает работу)
q0 - заключительное состояние (машина закончила работу)
Символы {П, Л, Н!} – символы сдвига (вправо, влево, на месте)
Устройство машины Тьюринга
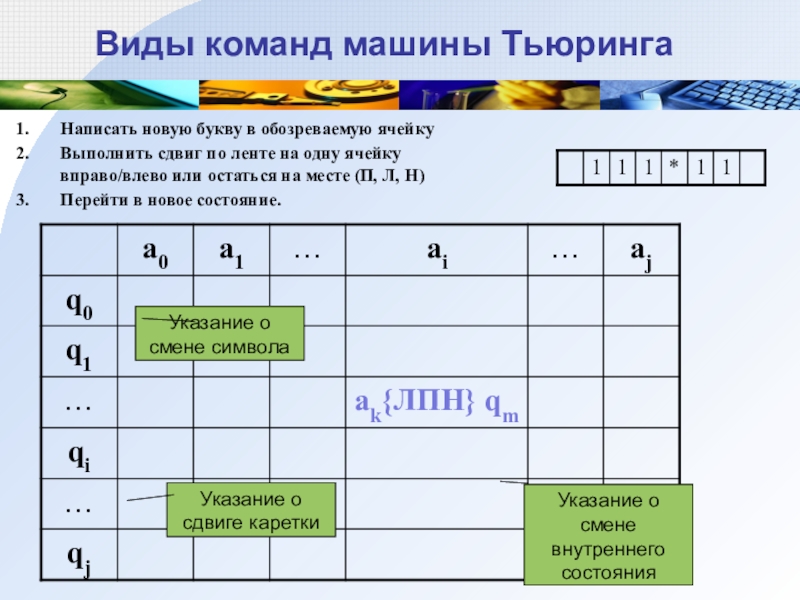
Слайд 6Виды команд машины Тьюринга
Написать новую букву в обозреваемую ячейку
Выполнить сдвиг по
Перейти в новое состояние.
Указание о смене символа
Указание о сдвиге каретки
Указание о смене внутреннего состояния
Слайд 7
3) Внешняя память (лента)
Машина имеет ленту, разбитую на ячейки, в каждую
Устройство машины Тьюринга
Слайд 8
3) Внешняя память (лента)
Устройство машины Тьюринга
Пустая клетка содержит a0.
В каждый
Лента является конечной, но дополняется в любой момент ячейками слева и справа для записи новых непустых символов.
Это соответствует принципу абстракции потенциальной осуществимости
Слайд 9
4) Каретка (управляющая головка)
Каретка машины располагается над некоторой ячейкой ленты –
В одном такте работы каретка сдвигается на одну ячейку (вправо, влево) или остается на месте
Устройство машины Тьюринга
Слайд 10
5) Функциональная схема (программа)
Программа машины состоит из команд:
Устройство машины Тьюринга
Для каждой
Слайд 11
К началу работы машины на ленту подается исходный набор данных в
Описание работы машины Тьюринга
Будем говорить, что непустое слово α в алфавите А\{a0} воспринимается машиной в стандартном положении, если:
- оно задано в последовательных ячейках ленты,
- все другие ячейки пусты,
- машина обозревает крайнюю правую ячейку из тех, в которых записано слово α
Слайд 12
Описание работы машины Тьюринга
Стандартное положение называется начальным (заключительным), если машина, воспринимающая
Слайд 13Находясь в не заключительном состоянии, машина совершает шаг, который определяется текущим
Описание работы машины Тьюринга
Слайд 14
Описание работы машины Тьюринга
В соответствии с командой qiaj → qkal Х
1) Содержимое обозреваемой ячейки aj стирается и в нее записывается символ al (который может совпадать с aj)
2) Машина переходит в новое состояние qk (оно может совпадать с состоянием qi)
3) Каретка перемещается в соответствии с управляемым символом Х ∈ {П, Л, Н!}
Слайд 15При переходе машины в заключительное состояние q0 ее работа прекращается
На ленте
Описание работы машины Тьюринга
Слайд 16
Машинным словом (конфигурацией) машины Тьюринга называется слово вида α1qkal α2, где
Слайд 17Конфигурация α1qkal α2 интерпретируется следующим образом:
- машина находится в состоянии qk
-
- α1 и α2 – это содержимое ленты до и после символа al
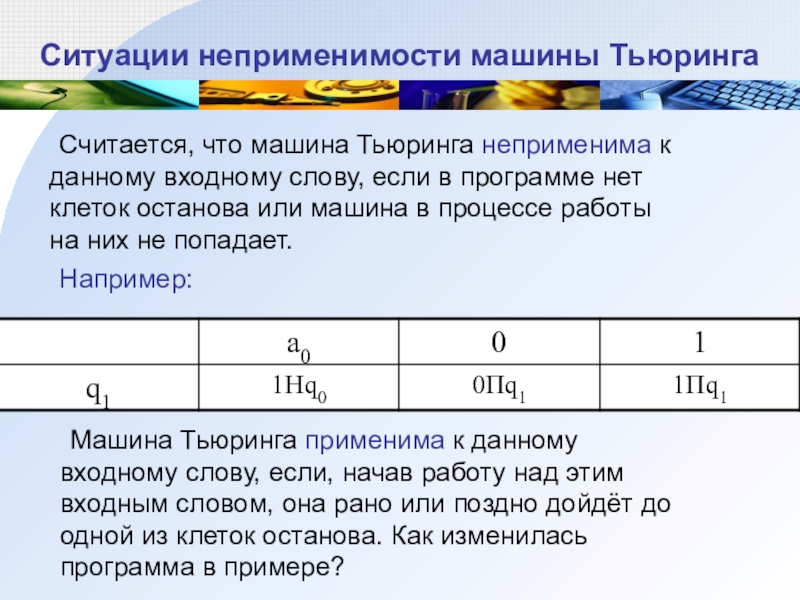
Слайд 18Ситуации неприменимости машины Тьюринга
Считается, что машина Тьюринга неприменима к данному входному
Например:
Машина Тьюринга применима к данному входному слову, если, начав работу над этим входным словом, она рано или поздно дойдёт до одной из клеток останова. Как изменилась программа в примере?
Слайд 19Пример машин Тьюринга
Требуется построить машину Тьюринга для решения следующей задачи: во
у
→
у
б
→
а
а
→
б
р
→
р
у
б
а
р
а
б
а
→
б
б
→
а
а
б
б
а
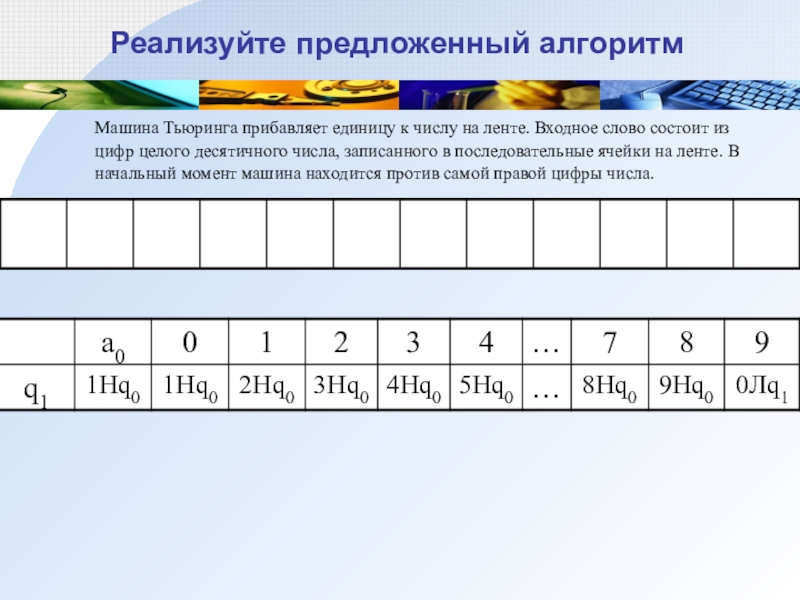
Слайд 20Реализуйте предложенный алгоритм
Машина Тьюринга прибавляет единицу к числу на ленте. Входное
Слайд 21Реализуйте предложенный алгоритм
На ленте машины Тьюринга содержится последовательность символов «+». Машина
q1 – машина ищет правый конец числа;
q2 – пропускает знак «+», при достижении конца последовательности – останов;
q3 – знак «+» заменяет на «–».
Слайд 22Пример
Дана машина Тьюринга с внешним алфавитом А = {a0, 1, *
Применить машину Тьюринга к слову α=11*1, начиная со стандартного начального положения
Слайд 32Литература
Игошин В.И. Математическая логика и теория алгоритмов. – М.: Академия, 2008.
Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. – СПб.: Лань, 1999. - 288 с.
Ильиных А.П. Теория алгоритмов. Учебное пособие. – Екатеринбург, 2006. - 149 с.