- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Логика 10кл.
Содержание
- 1. Презентация по теме Логика 10кл.
- 2. План изучения темы включает следующие вопросыПонятие о
- 3. Этапы развития логики 1.1.&
- 4. Предмет логики Логика (др.-греч. «λογική» — «искусство рассуждения») — наука, изучающая законы и формы мышления.
- 5. Слайд 5
- 6. 1-й этап: ФОРМАЛЬНАЯ ЛОГИКАсвязан с работами ученого
- 7. 2-й этап : появление математической или символической
- 8. 3 этап: становление математической логики самостоятельной наукой
- 9. 4 этап: использование элементов логики для построения
- 10. Слайд 10
- 11. ФОРМАЛЬНАЯ ЛОГИКА связана с анализом наших обычных
- 12. Формы человеческого мышления 1.2.&
- 13. Понятие форма мышления, в которой отражаются отличительные существенные признаки предметов
- 14. СУЩЕСТВЕННЫЕ ПРИЗНАКИ – это такие признаки, каждый
- 15. ПОНЯТИЕ характеризуетсяСодержаниемОбъемомСодержание – совокупность существенных признаков, отраженных
- 16. Река - Большой объем водыВода преснаяИмеет исток и устьесодержаниеРеки Лена, Обь, Енисей, Амазонка и т.д. объем
- 17. Суждение- форма мышления, в которой что-либо утверждается
- 18. Логическая форма суждения- это его строение, способ
- 19. Логическая форма сужденияЭто субъект, или то, о
- 20. Умозаключение- форма мышления, посредством которой из одного
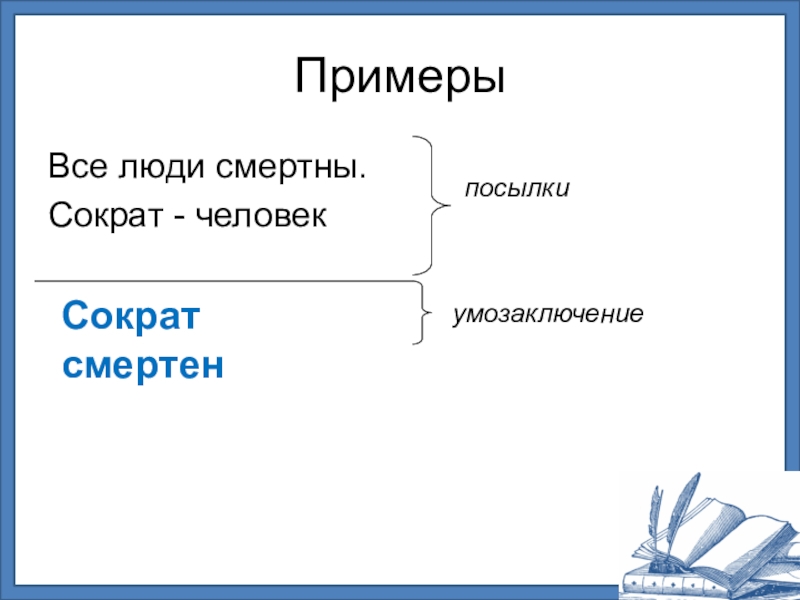
- 21. Примеры Все люди смертны.Сократ - человекСократ смертенпосылкиумозаключение
- 22. Если цветы поливают, то они не засохнутЦветы
- 23. Все граждане России имеют право на отдыхЯ – имею право на отдыхЯ - гражданин России
- 24. «Кондотьеры по-разному владеют своим ремеслом: одни -
- 25. Кондотьеры по-разному владеют своим ремеслом: одни -
- 26. Первым нельзя довериться, потому что они сами
- 27. (греч. Syllogysmos «вывод»)СиллогизмыВ силлогизмы входят три
- 28. Ложные силлогизмыМеталл проводит токВода проводит токВода -
- 29. Правила терминовВ силлогизме должно быть ровно 3
- 30. • Из двух отрицательных посылок не следует
- 31. • У 1ф первая посылка должна быть
- 32. (греч. sophisma - хитрая уловка, измышление) -
- 33. Алгебраический софизмПредположим: умножаем обе части уравнения на
- 34. Софизм - песенка английских студентов Чем
- 35. Парадокс – противоречие возникающее при сохранении
- 36. Гравюры Эшера
- 37. Слайд 37
- 38. ЗаданияОпределить объем и содержание понятий: столица, город,
- 39. Алгебра логики. Высказывания. 1.3.&
- 40. Алгебра логики - - это раздел математической
- 41. Высказывание- это повествовательное предложение, относительно которого можно
- 42. Высказывания бывают:ПростыеСоставные ИстинныеЛожные Составные высказывания образуются из
- 43. Сложное высказываниеПростым – высказывание, которое не содержит
- 44. Например:А= на улице светит солнцеВ= на улице
- 45. Пример 2:А=Я получу 2В = я выучу
- 46. Логические операции 1.4.&
- 47. Операция НЕ (инверсия)Если высказывание A истинно, то
- 48. Операция И (логическое умножение, конъюнкция)10также: A &
- 49. Операция ИЛИ (логическое сложение, дизъюнкция)10также: A+B, A
- 50. Импликация («если …, то …»)A =«На улице
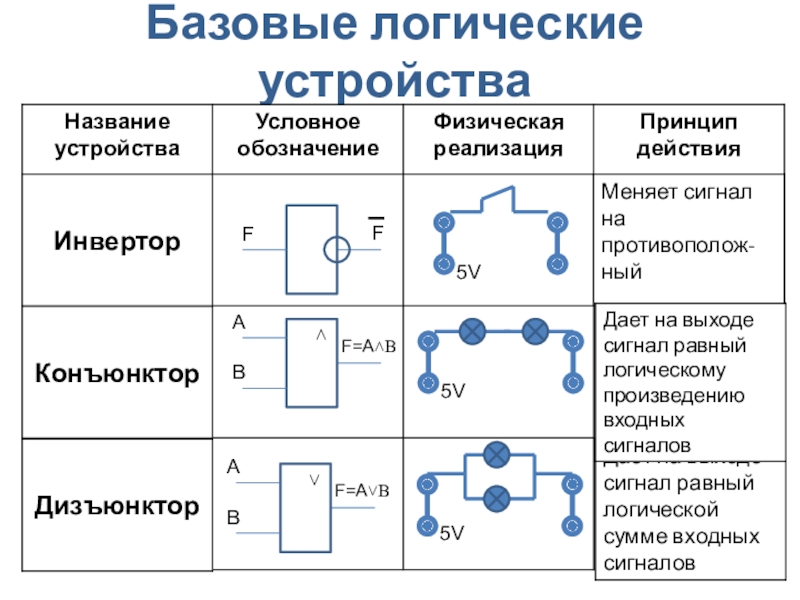
- 51. Эквиваленция («тогда и только тогда, …»)Высказывание «A
- 52. Построение таблиц истинности сложных высказываний1.5.&
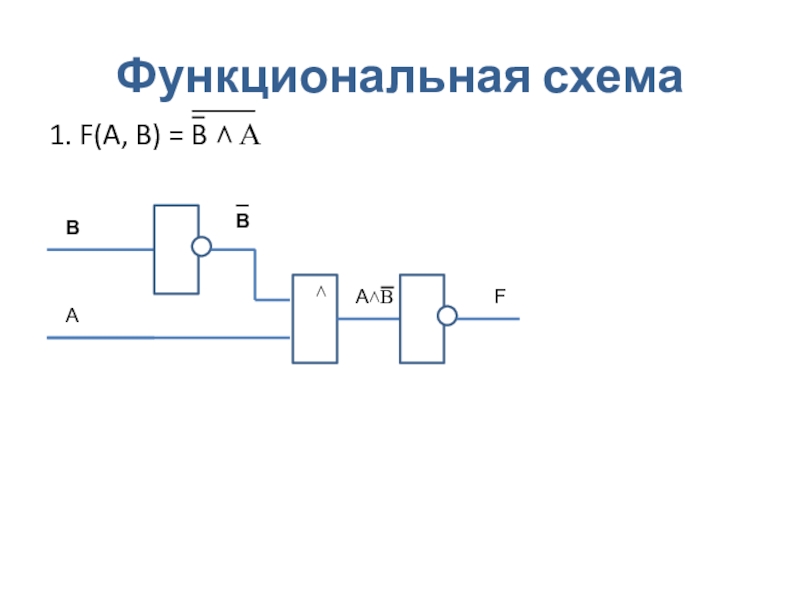
- 53. Приоритет логических операцийИнверсияКонъюнкцияДизъюнкцияИмпликацияЭквивалентностьПри наличие скобок – вначале выполняются действия в скобках
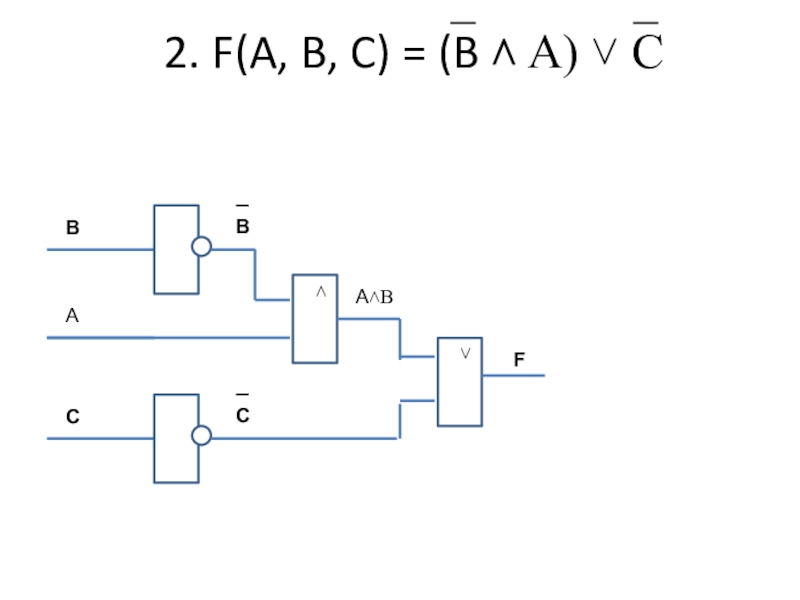
- 54. 1.Порядок действий2. Переменные n3. Строк = 2n+14.
- 55. Расставить действия по порядку
- 56. Построить таблицу истинности
- 57. Слайд 57
- 58. Проверьте равносильность с помощью таблиц истинности112321vC31v2
- 59. Задания на применение Логических операций1.5.&
- 60. 1. Дан фрагмент таблицы истинности выражения F
- 61. 2. Дан фрагмент таблицы истинности выражения FКакое
- 62. 3.
- 63. 1в-т2 в-т
- 64. 1в-т2 в-т
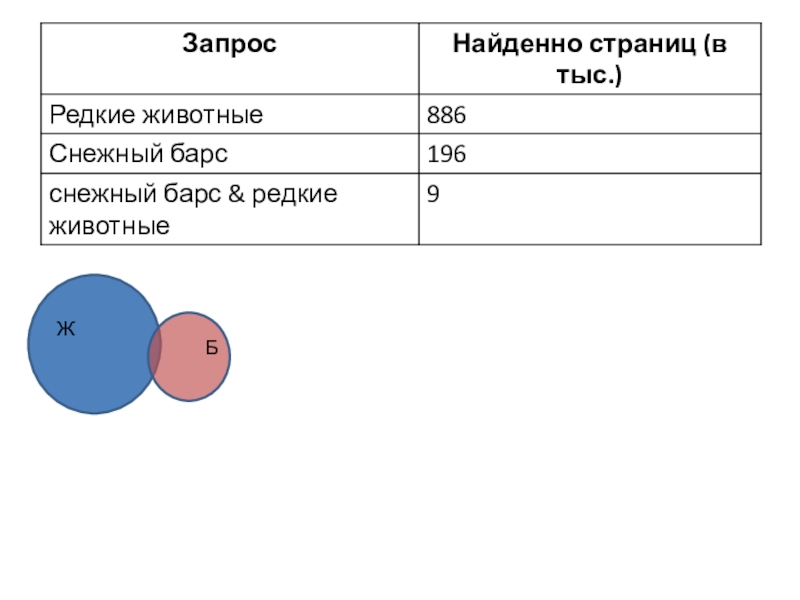
- 65. Круги эйлера
- 66. КЛ
- 67. Слайд 67
- 68. Слайд 68
- 69. ЖБ
- 70. Слайд 70
- 71. Законы логики1.5.&
- 72. Закон тождестваЗакон непротиворечия Закон исключения третьего
- 73. Закон двойного отрицанияСвойства констант
- 74. Закон коммутативностиЗакон ассоциативностиЗакон дистрибутивности
- 75. Закон де МорганаЗаконы поглощенияЗакон идемпотентности
- 76. 1. Упростить выражение:З-н де МорганаСочетательный и переместительный З-н непротиворечияЗ-н идемпотентности0
- 77. 2.З-н де МорганаЗ-н дистрибутивностиЗ-н исключения 3-гоСв-во констант: А˄1=А=1З-н исключения 3-го
- 78. 3.З-н де МорганаЗ-н двойного отрицания=1
- 79. Решение логических задач1.6.&
- 80. Методы решения:Метод графовТабличный методАлгебраический методМетод рассуждений
- 81. 1.Мальчики сказали следующее: Лева: Лена сделала рисунок,
- 82. 2.Синий стул стоит около красного и того,
- 83. 3.Иван живет не в МосквеАндрей – не
- 84. Слайд 84
- 85. РазминкаАлеша, Илья и Денис нашли в земле
- 86. Построение функциональных схем1.7.&
- 87. Базовые логические устройства
- 88. Составить схему устройстваДля голосования 3-х членов жюри.
- 89. Функциональная схема1. F(A, B) = B ˄ A˄ABBA˄BF
- 90. 2. F(A, B, C) = (B ˄ A) ˅ C ˄ABBA˄BCC˅F
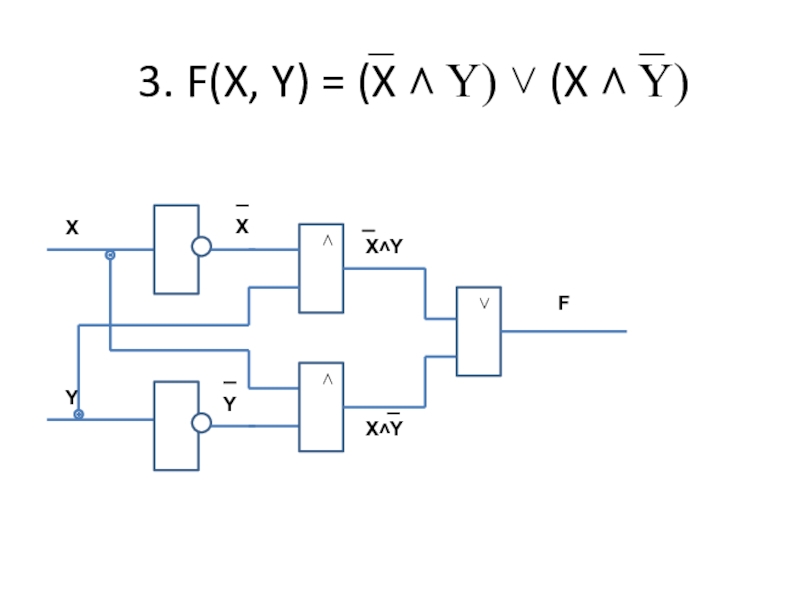
- 91. 3. F(X, Y) = (X ˄ Y) ˅ (X ˄ Y) YXXYX˄YX˄YF
- 92. 5. ?
- 93. План изучения темы включает следующие вопросыПонятие о
Слайд 2План изучения темы включает следующие вопросы
Понятие о логике как науке
Этапы развития
Высказывания. Истинные и ложные, простые и сложные высказывания. Связки И, ИЛИ и частица НЕ.
Алгебра логики
Основные понятия и область применения алгебры логики
Элементарные логические операции
Логические функции
Таблицы истинности
Задачи логики
Законы алгебры логики
Упрощение логических выражений.
Логические элементы ПК — И, ИЛИ, НЕ.
Построение функциональных схем по логическим функциям.
Слайд 4Предмет логики
Логика
(др.-греч. «λογική» — «искусство рассуждения») — наука,
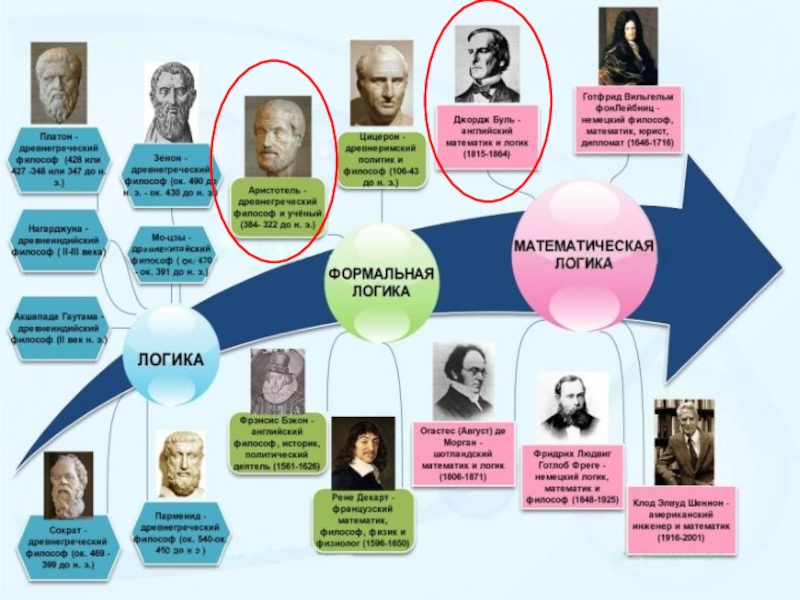
Слайд 61-й этап: ФОРМАЛЬНАЯ ЛОГИКА
связан с работами ученого и философа Аристотеля (384—322
Он пытался найти ответ на вопрос «как мы рассуждаем",
изучал правила мышления,
впервые дал систематическое изложение логики,
подверг анализу человеческое мышление,
Определил его формы —
понятие,
суждение,
умозаключение.
Так возникла формальная логика
Слайд 72-й этап : появление математической или символической логики
Основы ее заложил немецкий
Готфрид Вильгельм Лейбниц (1646—1716).
сделал попытку построить первые логические исчисления (свести логику к математике)
Предложил использовать символы вместо слов обычного языка
начал распространение логики за рамки гуманитарных наук
Слайд 83 этап: становление математической логики самостоятельной наукой
развил идею окончательно англичанин
Буль считается основоположником математической логики как самостоятельной дисциплины.
В его работах логика обрела свой алфавит, свою орфографию и грамматику.
Начальный раздел математической логики называют
алгеброй логики
или
булевой алгеброй.
Слайд 94 этап: использование элементов логики для построения компьютера
Данный этап связан с
Сформулировал принципы архитектуры ЭВМ
Обосновал использование двоичной системы для хранения информации
Слайд 11ФОРМАЛЬНАЯ ЛОГИКА
связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным
МАТЕМАТИЧЕСКАЯ ЛОГИКА
изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода.
Слайд 14СУЩЕСТВЕННЫЕ ПРИЗНАКИ –
это такие признаки, каждый из которых, взятый отдельно, необходим,
Слайд 15ПОНЯТИЕ характеризуется
Содержанием
Объемом
Содержание – совокупность существенных признаков, отраженных в этом понятии.
Объем –
Слайд 16Река -
Большой объем воды
Вода пресная
Имеет исток и устье
содержание
Реки Лена, Обь,
объем
Слайд 17Суждение
- форма мышления, в которой что-либо утверждается или отрицается о предметах,
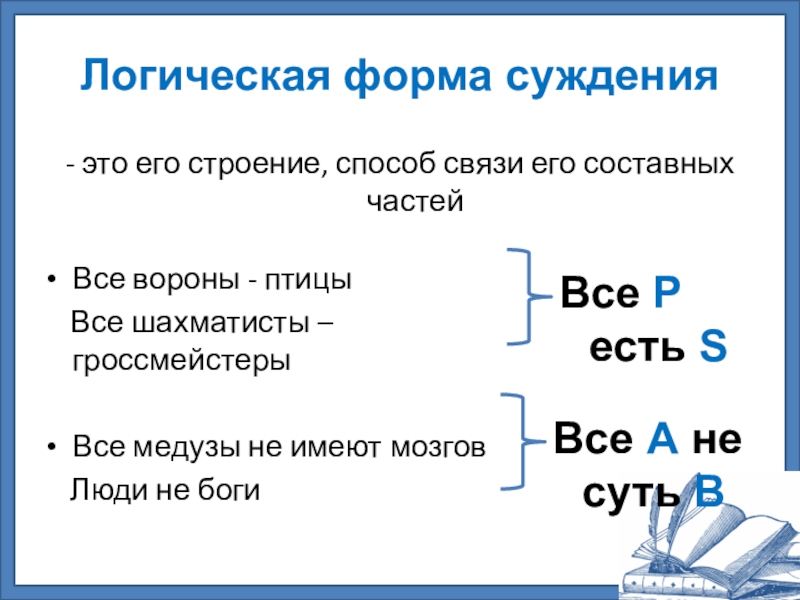
Слайд 18Логическая форма суждения
- это его строение, способ связи его составных частей
Все
Все шахматисты – гроссмейстеры
Все медузы не имеют мозгов
Люди не боги
Все Р есть S
Все A не суть B
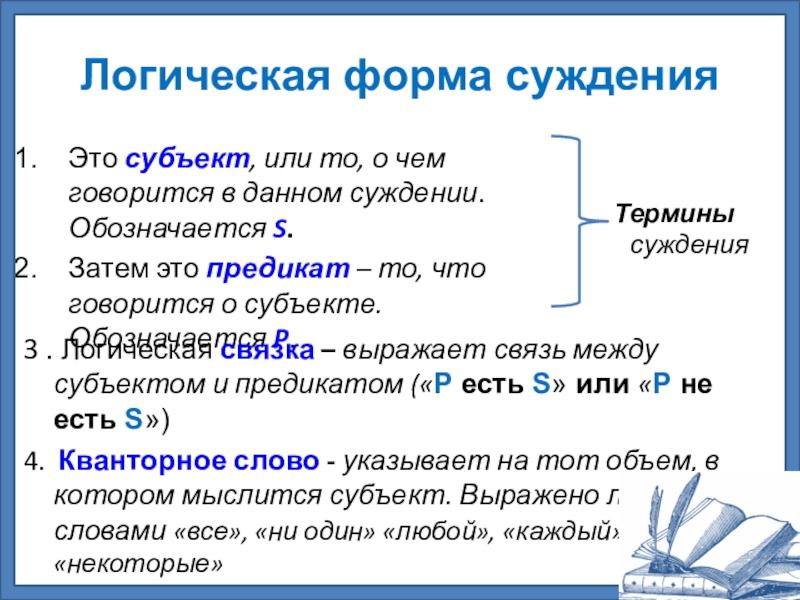
Слайд 19Логическая форма суждения
Это субъект, или то, о чем говорится в данном
Затем это предикат – то, что говорится о субъекте. Обозначается P.
3 . Логическая связка – выражает связь между субъектом и предикатом («Р есть S» или «Р не есть S»)
4. Кванторное слово - указывает на тот объем, в котором мыслится субъект. Выражено либо словами «все», «ни один» «любой», «каждый», «некоторые»
Термины суждения
Слайд 20Умозаключение
- форма мышления, посредством которой из одного или нескольких суждений, называемых
Слайд 22Если цветы поливают, то они не засохнут
Цветы засохли
Все граждане России имеют
Я – гражданин России
Цветы не поливали
Я имею право на отдых
Слайд 24«Кондотьеры по-разному владеют своим ремеслом: одни - превосходно, другие – посредственно.
(Макиавелли).
Слайд 25Кондотьеры по-разному владеют своим ремеслом: одни - превосходно, другие – посредственно
Некоторые
Некоторые кондотьеры владеют ремеслом посредственно
Некоторые S есть P1
Некоторые S есть P2
Кондотьеры владеют ремеслом или превосходно, или посредственно
S есть P1 или Р2
Слайд 26Первым нельзя довериться, потому что они сами будут домогаться власти…
Если кондотьер
1 посылка
Если кондотьер владеет ремеслом превосходно, то он будет добиваться власти
2 посылка
Вывод
Кондотьеру нельзя доверять
Слайд 27 (греч. Syllogysmos «вывод»)
Силлогизмы
В силлогизмы входят три суждения (две посылки и
1. Меньшим термином (S) является субъект того суждения, которое получилось в качестве вывода.
2. Больший термин (P) предикат вывода.
3. Средний термин (M) входит в обе посылки, но отсутствует в выводе.
Слайд 28Ложные силлогизмы
Металл проводит ток
Вода проводит ток
Вода - металл
Все зулусы – люди.
Мы
Мы все - зулусы
P есть М
S есть М
S есть P
Слайд 29Правила терминов
В силлогизме должно быть ровно 3 термина.
• Средний термин должен
• Если термин не взят в полном объёме в посылке, то он не может быть взят в полном объёме и в выводе.
Некоторые живые существа ядовиты.
Котики — это живые существа.
Котики ядовиты
Некоторые M есть Р
Некоторые S есть М
Некоторые S есть Р
Все змеи рода аспидовых ядовиты.
Кобра — это змея рода аспидовых .
Кобры ядовиты
Слайд 30• Из двух отрицательных посылок не следует никакого вывода.
• Если одна
• Из двух частных посылок не следует никакого вывода.
Правила посылок
Люди не птицы.
Собаки не люди.
?
Все боксеры — спортсмены.
Некоторые люди — боксеры.
?
Слайд 31• У 1ф первая посылка должна быть общим суждением, а меньшая
• У 2ф P должна быть общим суждением, а S и заключение отрицательными.
• У 3ф S должна быть утвердительным суждением, а заключение частным.
• У 4ф два правила:
если M является утвердительным суждением, то S должна быть общим суждением;
если одна из посылок отрицательная, то P должна быть общей.
Правила фигур
Слайд 32(греч. sophisma - хитрая уловка, измышление) - рассуждение, кажущееся правильным, но
Софизм
Слайд 33Алгебраический софизм
Предположим:
умножаем обе части уравнения на "а".
Отнимаем от обеих
Преобразуем уравнение
Сокращаем обе части уравнения на (a — b)
Так как а = b, заменяем в левой части а на b
Сокращаем на b.
а = b
a x a = a х b,
a2 = ab
a2 — b2 = ab — b2
(a + b) (a — b) = b (a — b)
a + b = b
b + b = b
2b = b
2 = 1.
Слайд 34Софизм - песенка английских студентов
Чем больше учишься, тем
Слайд 35Парадокс –
противоречие возникающее при сохранении логической правильности рассуждения
Парадокс Б. Рассела
Слайд 38Задания
Определить объем и содержание понятий: столица, город, бесконечность
Вывести заключения, выявить логическую
а) Тем, кто лыс, расческа не нужна.
Ни одна ящерица не имеет волос.
б) Некоторые уроки трудны.
Все что трудно требует внимания.
В) Ни один добрый поступок не является незаконным
Все что законно можно делать без страха
Слайд 40Алгебра логики -
- это раздел математической логики, изучающий строение сложных
Слайд 41Высказывание
- это повествовательное предложение, относительно которого можно сказать истинно оно или
Например:
А = Днем светит солнце = 1
В = У каждого человека 5 ног = 0
С = Кто выучил уроки? –
D = х>5 –
Слайд 42Высказывания
бывают:
Простые
Составные
Истинные
Ложные
Составные высказывания образуются из простых путем соединения их с
Слайд 43Сложное высказывание
Простым –
высказывание, которое не содержит в себе других высказываний
Если
сложным
Слайд 44Например:
А= на улице светит солнце
В= на улице идет дождь
Е=А и В=
F=А и неВ = На улице светит солнце и нет дождя
Слайд 45Пример 2:
А=Я получу 2
В = я выучу уроки
С = Меня спросят
E
= Если я выучу уроки или меня не спросят, то я не получу 2.
F = Я получу 2, если я не выучу уроки и меня спросят.
F = Если не В и С, то А
Слайд 47Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
1
0
0
1
также: , ⌐ А
not A (Паскаль),
Таблица истинности логического выражения Х
– это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.
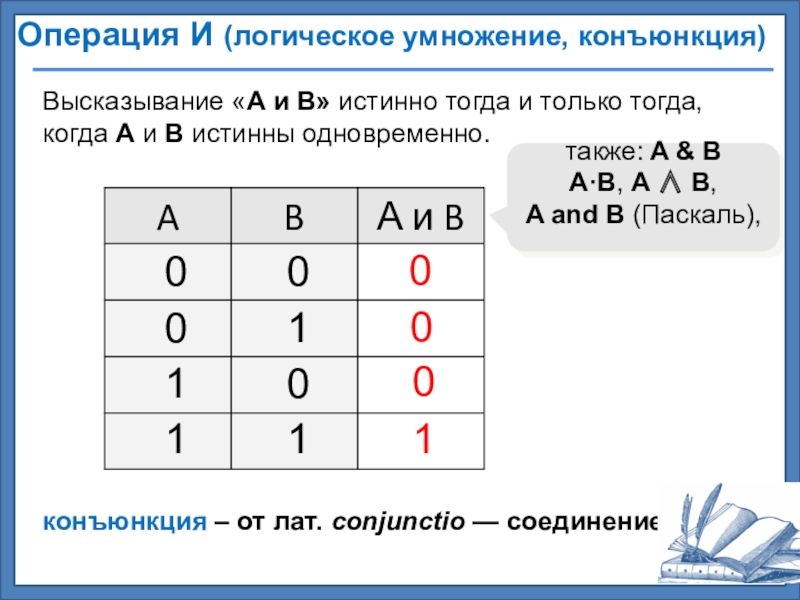
Слайд 48Операция И (логическое умножение, конъюнкция)
1
0
также: A & B
A·B, A B,
A
0
0
конъюнкция – от лат. conjunctio — соединение
Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны одновременно.
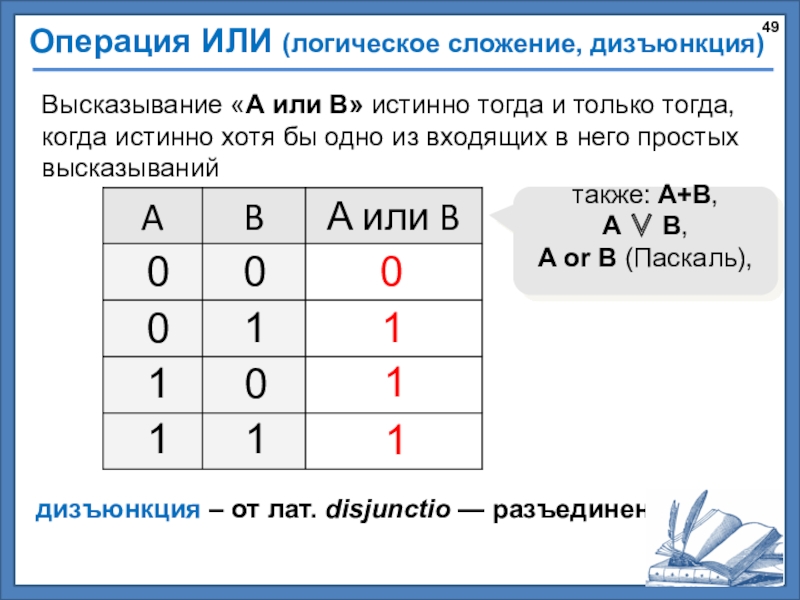
Слайд 49Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
также: A+B,
A B,
A or B
1
1
дизъюнкция – от лат. disjunctio — разъединение
Высказывание «A или B» истинно тогда и только тогда, когда истинно хотя бы одно из входящих в него простых высказываний
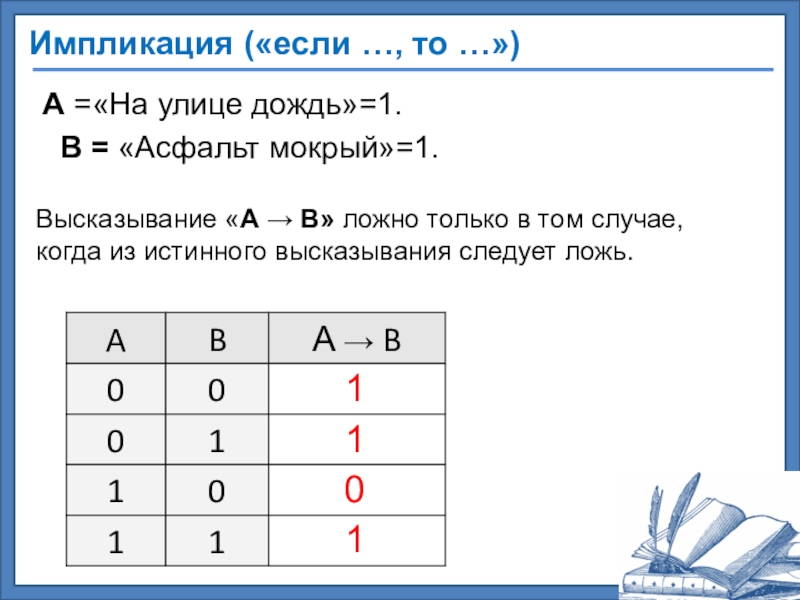
Слайд 50Импликация («если …, то …»)
A =«На улице дождь»=1.
B = «Асфальт
1
1
1
0
Высказывание «A B» ложно только в том случае, когда из истинного высказывания следует ложь.
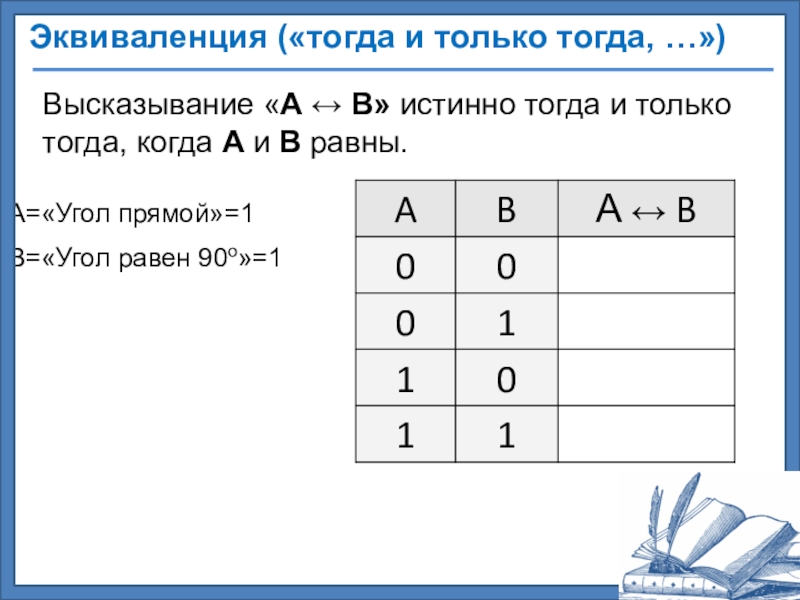
Слайд 51Эквиваленция («тогда и только тогда, …»)
Высказывание «A B» истинно тогда
А=«Угол прямой»=1
В=«Угол равен 90о»=1
Слайд 53Приоритет логических операций
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность
При наличие скобок – вначале выполняются действия в скобках
Слайд 541.Порядок действий
2. Переменные n
3. Строк = 2n+1
4. Столбцов = n +
5. начертить таблицу
6. В первую строку: переменные, действия по порядку
7. Комбинации значений переменных
8. Выполняем действия
9. Делаем вывод об истинности
высказывания
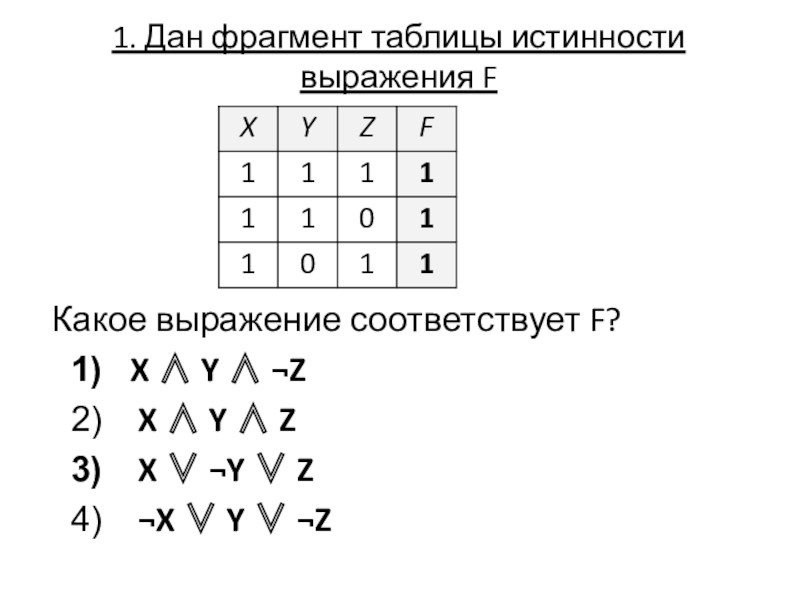
Слайд 601. Дан фрагмент таблицы истинности выражения F
Какое выражение соответствует F?
X
X Y Z
X ¬Y Z
¬X Y ¬Z
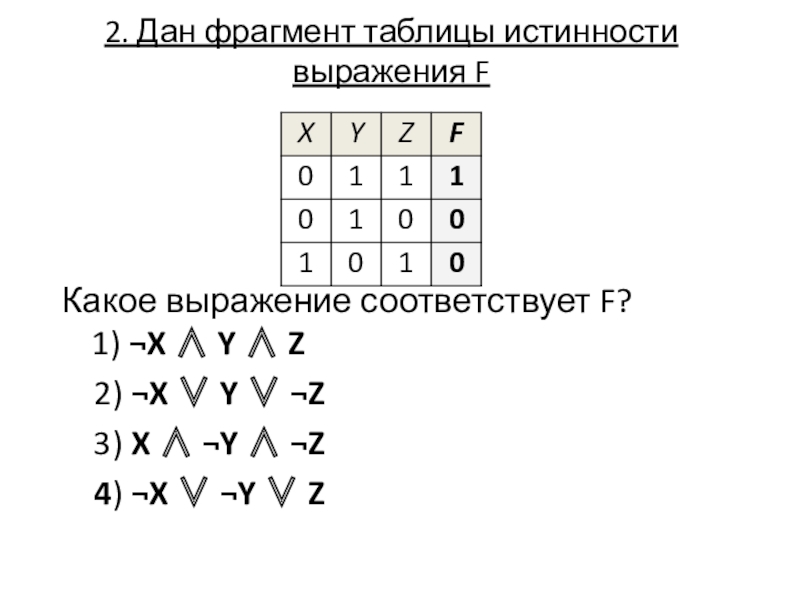
Слайд 612. Дан фрагмент таблицы истинности выражения F
Какое выражение соответствует F?
1) ¬X
2) ¬X Y ¬Z
3) X ¬Y ¬Z
4) ¬X ¬Y Z
Слайд 761. Упростить выражение:
З-н де Моргана
Сочетательный и переместительный
З-н непротиворечия
З-н идемпотентности
0
Слайд 772.
З-н де Моргана
З-н дистрибутивности
З-н исключения 3-го
Св-во констант: А˄1=А
=1
З-н исключения 3-го
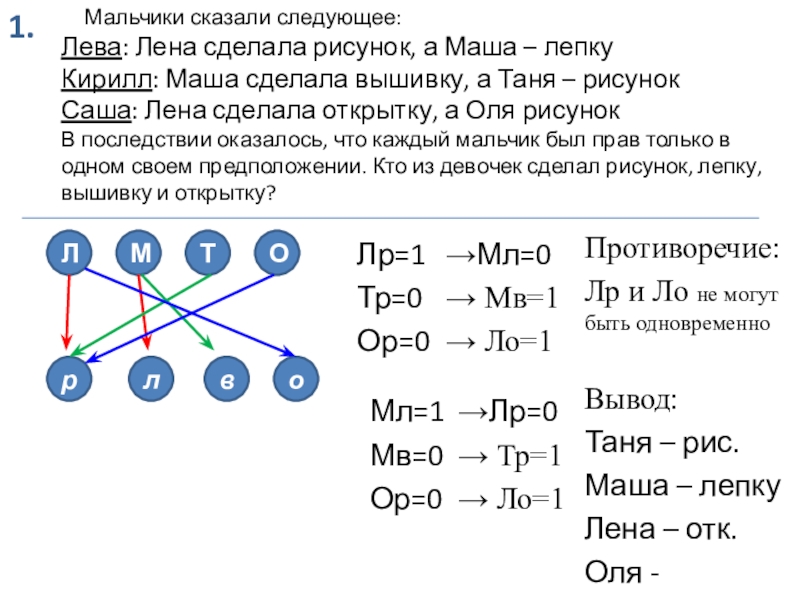
Слайд 811.
Мальчики сказали следующее:
Лева: Лена сделала рисунок, а Маша – лепку
Кирилл: Маша
Л
М
Т
О
о
в
л
р
Лр=1
Тр=0
Ор=0
→Мл=0
→ Мв=1
→ Ло=1
Противоречие:
Лр и Ло не могут быть одновременно
Мл=1
Мв=0
Ор=0
→Лр=0
→ Тр=1
→ Ло=1
Вывод:
Таня – рис.
Маша – лепку
Лена – отк.
Оля - вышивку
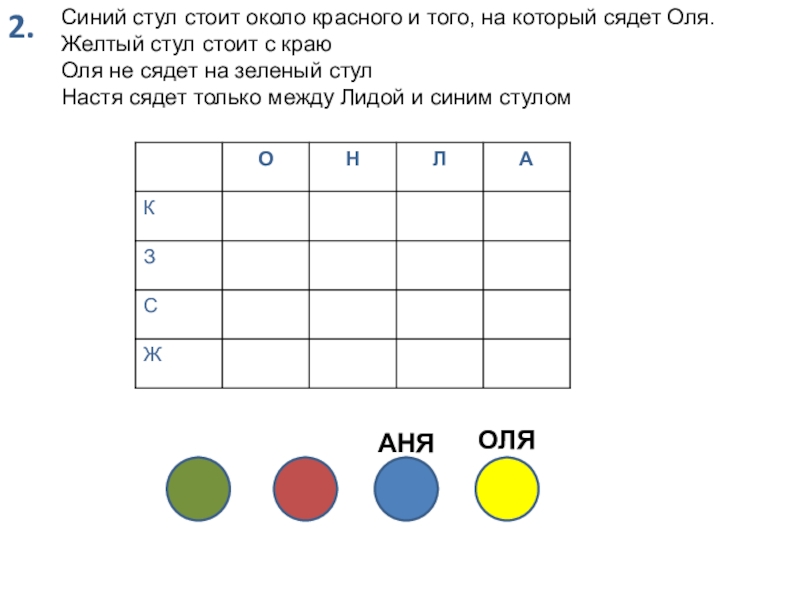
Слайд 822.
Синий стул стоит около красного и того, на который сядет Оля.
Желтый
Оля не сядет на зеленый стул
Настя сядет только между Лидой и синим стулом
ОЛЯ
АНЯ
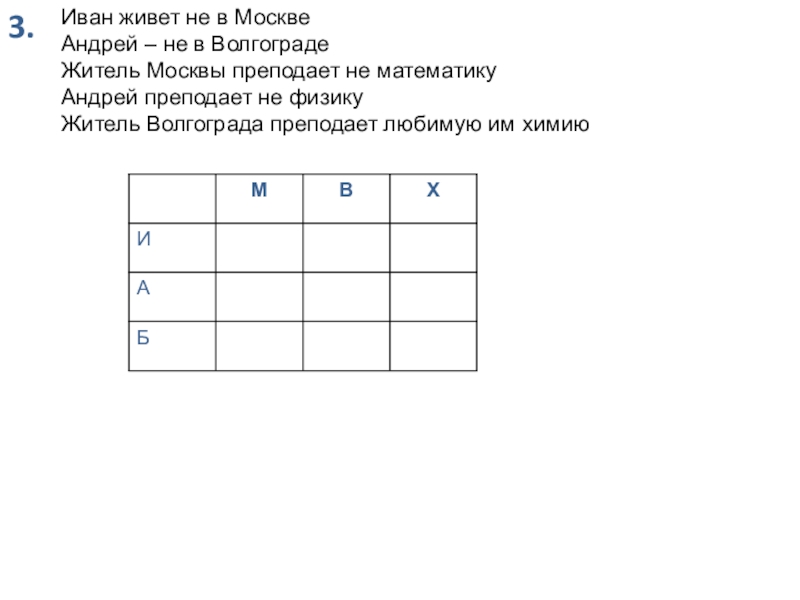
Слайд 833.
Иван живет не в Москве
Андрей – не в Волгограде
Житель Москвы преподает
Андрей преподает не физику
Житель Волгограда преподает любимую им химию
Слайд 85Разминка
Алеша, Илья и Денис нашли в земле хорошо сохранившееся древнее украшение.
Алеша: Это украшение греческое и относится к 5 в. До н.э
Илья: Это украшение египетское и относится к 10 в до н.э
Денис: Это украшение не греческое и относится к 7 в до н.э
После, профессор археологии сказал, что каждый юноша прав только в одном утверждении. Определите, где и в каком веке было создано украшение.
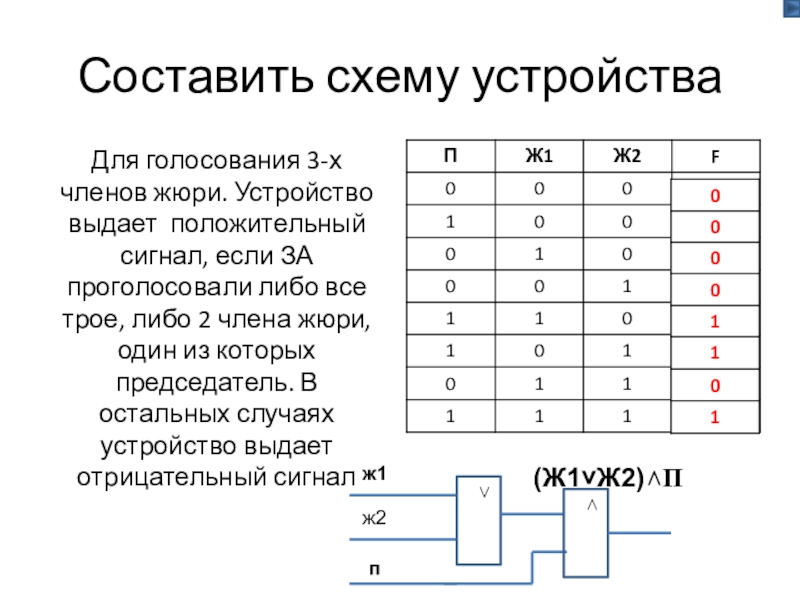
Слайд 88Составить схему устройства
Для голосования 3-х членов жюри. Устройство выдает положительный сигнал,
(Ж1˅Ж2)
˄П
ж1
п
ж2
Слайд 93План изучения темы включает следующие вопросы
Понятие о логике как науке (1—2
Этапы развития логики. (Презентация)
Высказывания. Истинные и ложные, простые и сложные высказывания. Связки И, ИЛИ и частица НЕ. (Самостоятельное изучение)
Алгебра логики (2—3 часа).
Основные понятия и область применения алгебры логики.
Логические функции.
Таблицы истинности.
Элементарные логические операции.
Задачи логики. (С разбором в классе)
Законы алгебры логики (1—3 часа).
Упрощение логических выражений.
Логические элементы ПК — И, ИЛИ, НЕ.
Построение функциональных схем по логическим функциям.
Требования:
Материал изучать желательно после тем:
Архитектура компьютера
Представление информации внутри компьютера.