Смоленск 2015
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Графы (основные понятия) для МДК 01.02 Математический аппарат для построения компьютерных сетей
Содержание
- 1. Презентация по теме Графы (основные понятия) для МДК 01.02 Математический аппарат для построения компьютерных сетей
- 2. Что такое граф?Как хранить графы?
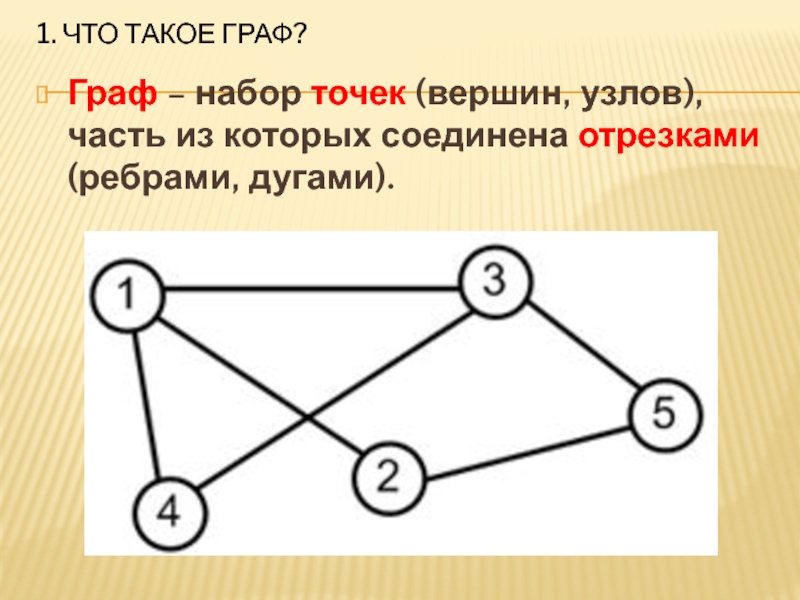
- 3. 1. Что такое граф?Граф – набор точек (вершин, узлов), часть из которых соединена отрезками (ребрами, дугами).
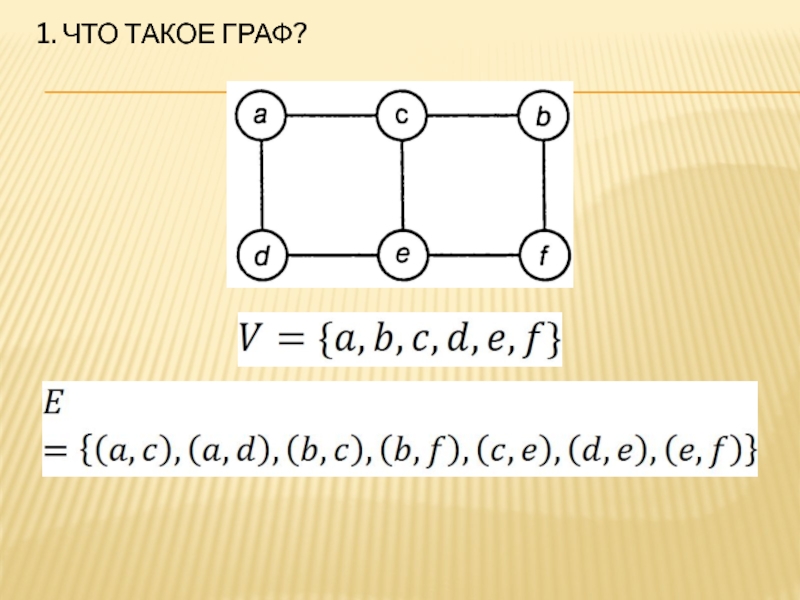
- 4. 1. Что такое граф?Граф определяется парой множеств:
- 5. 1. Что такое граф?
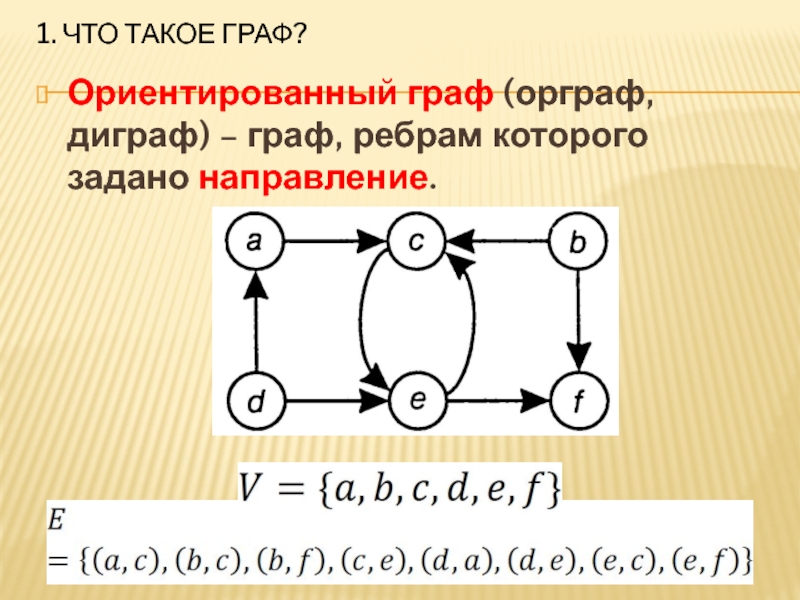
- 6. 1. Что такое граф?Ориентированный граф (орграф, диграф) – граф, ребрам которого задано направление.
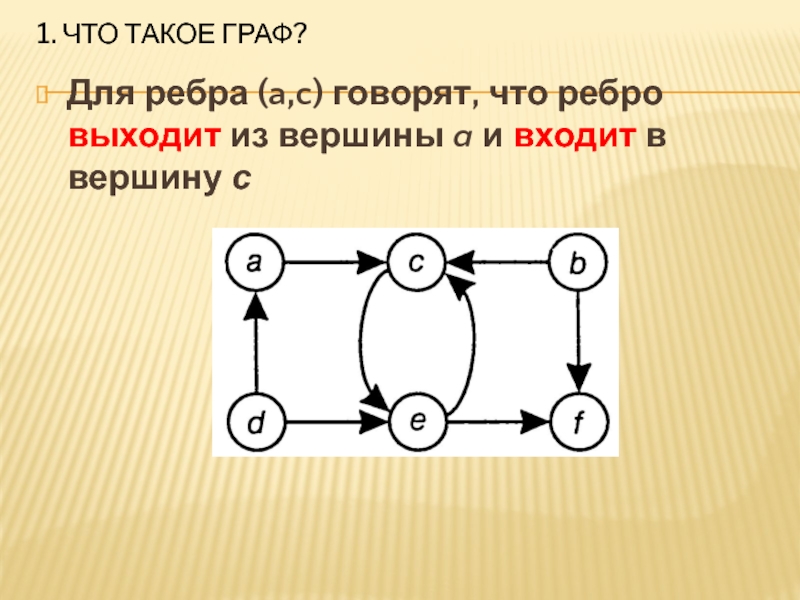
- 7. 1. Что такое граф?Для ребра (a,c) говорят,
- 8. 1. Что такое граф?Петля – ребро, которое соединяет вершину саму с собой.
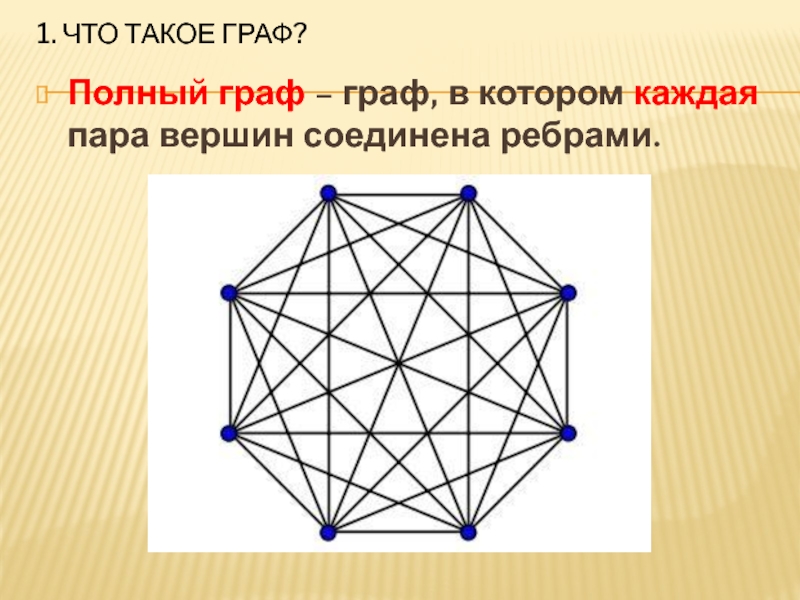
- 9. 1. Что такое граф?Полный граф – граф, в котором каждая пара вершин соединена ребрами.
- 10. 1. Что такое граф?Взвешенный граф – граф,
- 11. 1. Что такое граф?Путь от вершины a
- 12. 1. Что такое граф?Направленный путь от вершины
- 13. 1. Что такое граф?Длина пути - количество
- 14. 1. Что такое граф?Длина пути во взвешенном
- 15. 1. Что такое граф?Кратчайший путь в графе
- 16. 1. Что такое граф?Цикл – простой путь,
- 17. 1. Что такое граф?Связный граф – граф,
- 18. 1. Что такое граф?Связный компонент графа –
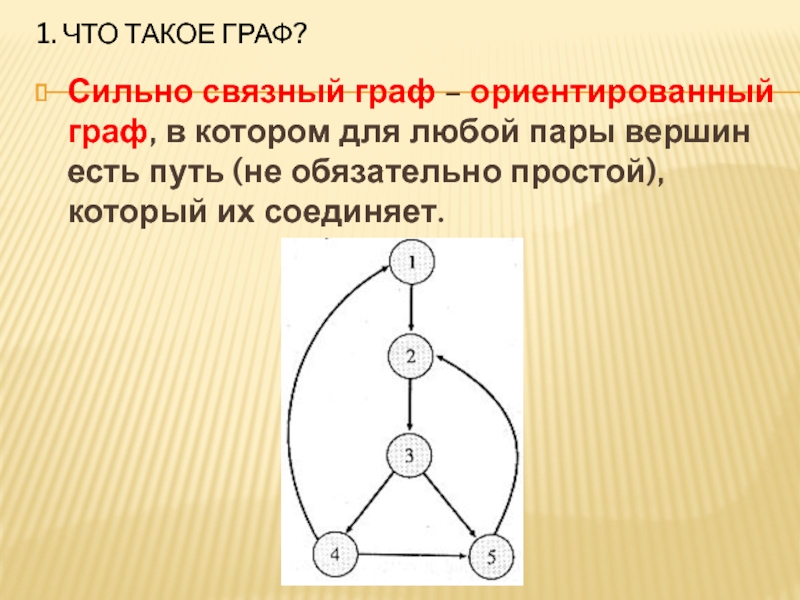
- 19. 1. Что такое граф?Сильно связный граф –
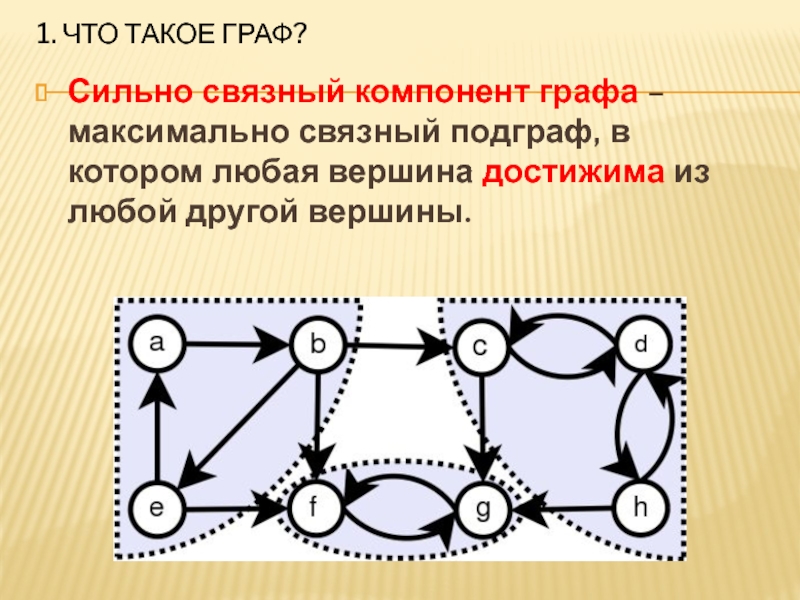
- 20. 1. Что такое граф?Сильно связный компонент графа
- 21. 1. Что такое граф?Плотный граф – граф,
- 22. 2. Как хранить графы?Граф хранится в виде: Матрицы смежности Списков смежности
- 23. 2. Как хранить графы?Матрица смежности для графа
- 24. 2. Как хранить графы?Списки смежности – массив
- 25. 2. Как хранить графы?Для взвешенного графаМатрица смежности
- 26. 2. Как хранить графы?Выбор способа хранения графа
- 27. 2. Как хранить графы?
Что такое граф?Как хранить графы?
Слайд 1Тема урока: «Графы (основные понятия)»
МДК 01.02 Математический аппарат для построения компьютерных
сетей
Слайд 31. Что такое граф?
Граф – набор точек (вершин, узлов), часть из
которых соединена отрезками (ребрами, дугами).
Слайд 41. Что такое граф?
Граф определяется парой множеств:
Конечное множество элементов V
(вершин)
Конечное множество элементов (ребер) E, каждый элемент содержит пару вершин (например (a,b))
Если вершины соединены ребром, они называются смежными.
Конечное множество элементов (ребер) E, каждый элемент содержит пару вершин (например (a,b))
Если вершины соединены ребром, они называются смежными.
Слайд 61. Что такое граф?
Ориентированный граф (орграф, диграф) – граф, ребрам которого
задано направление.
Слайд 71. Что такое граф?
Для ребра (a,c) говорят, что ребро выходит из
вершины a и входит в вершину с
Слайд 101. Что такое граф?
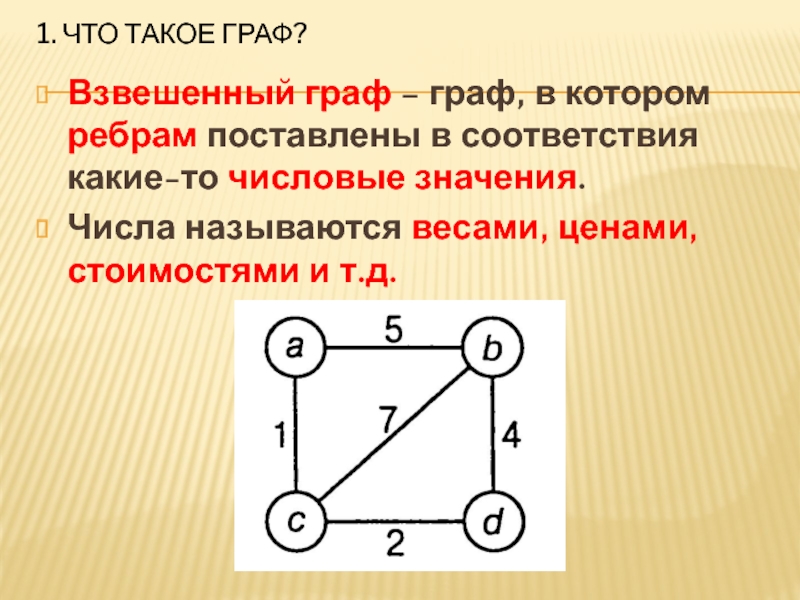
Взвешенный граф – граф, в котором ребрам поставлены
в соответствия какие-то числовые значения.
Числа называются весами, ценами, стоимостями и т.д.
Числа называются весами, ценами, стоимостями и т.д.
Слайд 111. Что такое граф?
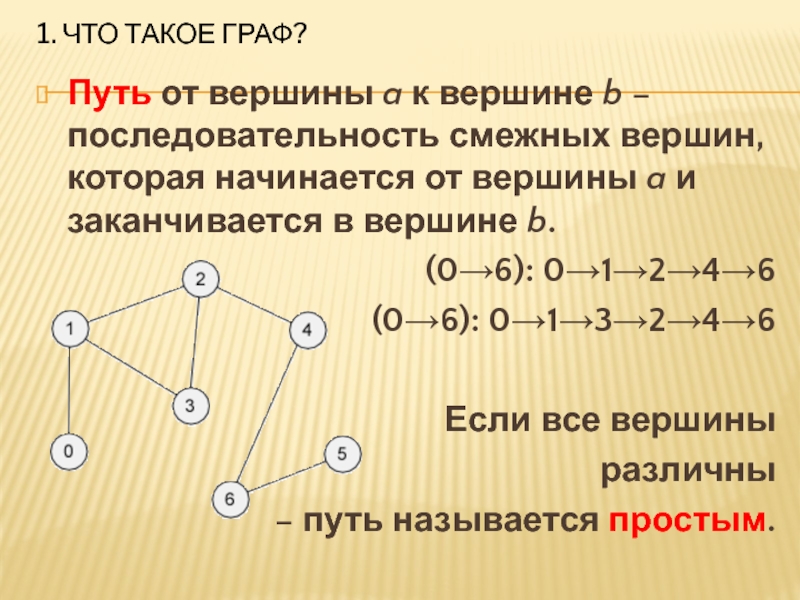
Путь от вершины a к вершине b –последовательность
смежных вершин, которая начинается от вершины a и заканчивается в вершине b.
(0→6): 0→1→2→4→6
(0→6): 0→1→3→2→4→6
Если все вершины
различны
– путь называется простым.
(0→6): 0→1→2→4→6
(0→6): 0→1→3→2→4→6
Если все вершины
различны
– путь называется простым.
Слайд 121. Что такое граф?
Направленный путь от вершины a к вершине b
– последовательность смежных вершин в ориентированном графе, которая начинается от вершины a и заканчивается в вершине b.
(1→6): 1→2→4→6
(1→6): 1→2→4→5→6
(1→6): 1→2→3→6
(1→6): 1→2→4→6
(1→6): 1→2→4→5→6
(1→6): 1→2→3→6
Слайд 131. Что такое граф?
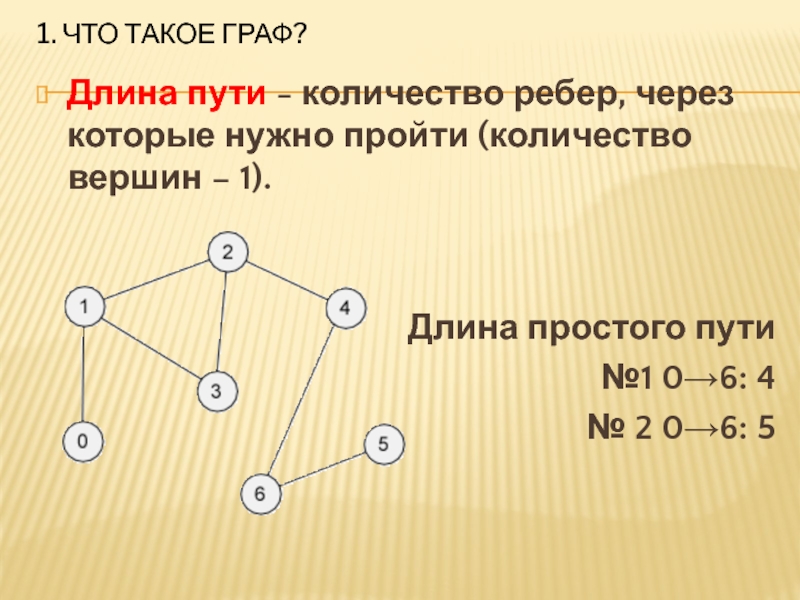
Длина пути - количество ребер, через которые нужно
пройти (количество вершин – 1).
Длина простого пути
№1 0→6: 4
№ 2 0→6: 5
Длина простого пути
№1 0→6: 4
№ 2 0→6: 5
Слайд 141. Что такое граф?
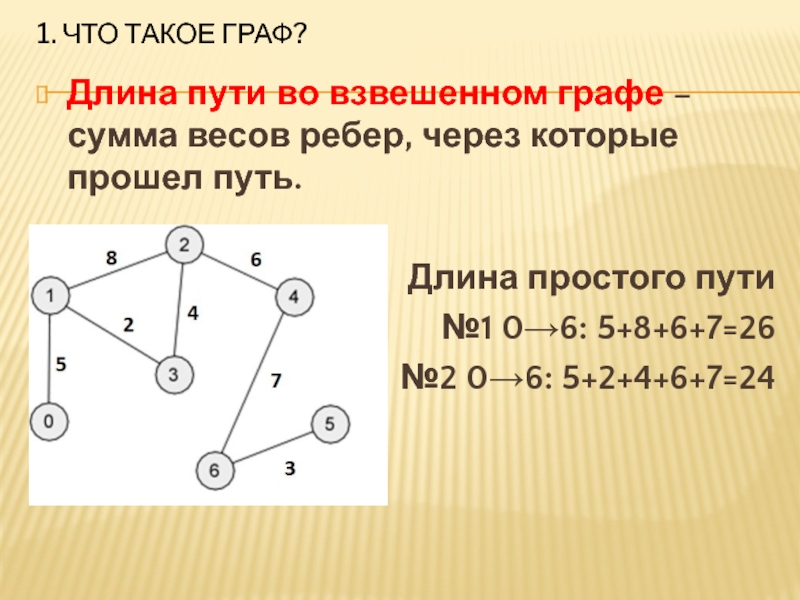
Длина пути во взвешенном графе – сумма весов
ребер, через которые прошел путь.
Длина простого пути
№1 0→6: 5+8+6+7=26
№2 0→6: 5+2+4+6+7=24
Длина простого пути
№1 0→6: 5+8+6+7=26
№2 0→6: 5+2+4+6+7=24
Слайд 151. Что такое граф?
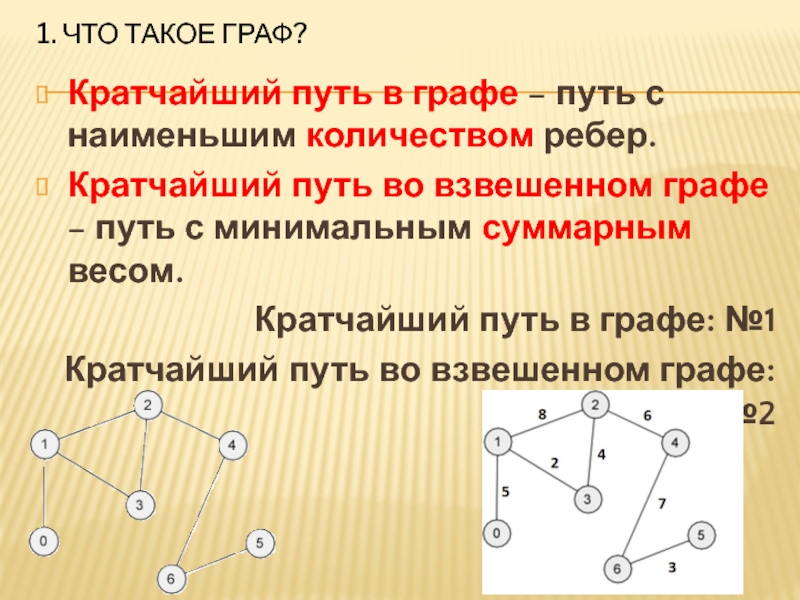
Кратчайший путь в графе – путь с наименьшим
количеством ребер.
Кратчайший путь во взвешенном графе – путь с минимальным суммарным весом.
Кратчайший путь в графе: №1
Кратчайший путь во взвешенном графе: №2
Кратчайший путь во взвешенном графе – путь с минимальным суммарным весом.
Кратчайший путь в графе: №1
Кратчайший путь во взвешенном графе: №2
Слайд 161. Что такое граф?
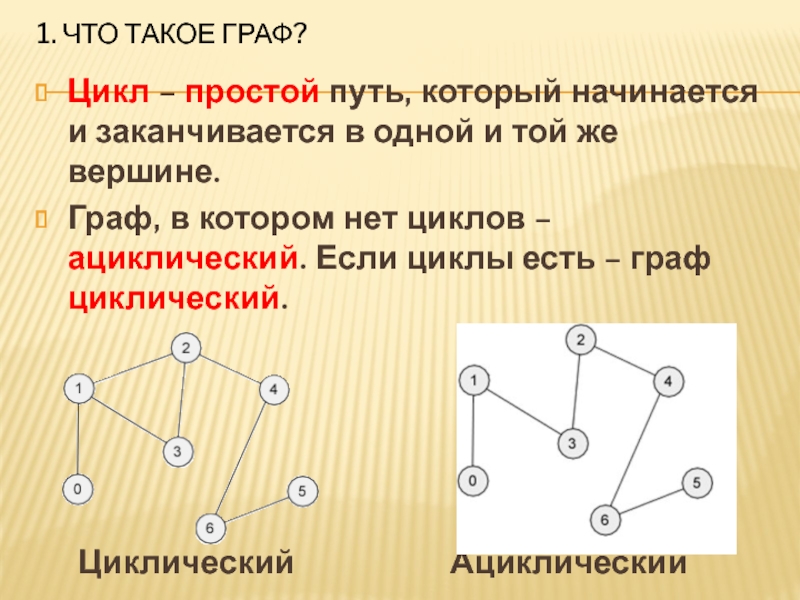
Цикл – простой путь, который начинается и заканчивается
в одной и той же вершине.
Граф, в котором нет циклов – ациклический. Если циклы есть – граф циклический.
Циклический Ациклический
Граф, в котором нет циклов – ациклический. Если циклы есть – граф циклический.
Циклический Ациклический
Слайд 171. Что такое граф?
Связный граф – граф, в котором для любой
пары вершин есть путь (не обязательно простой), который их соединяет.
Несвязный граф
Несвязный граф
Слайд 181. Что такое граф?
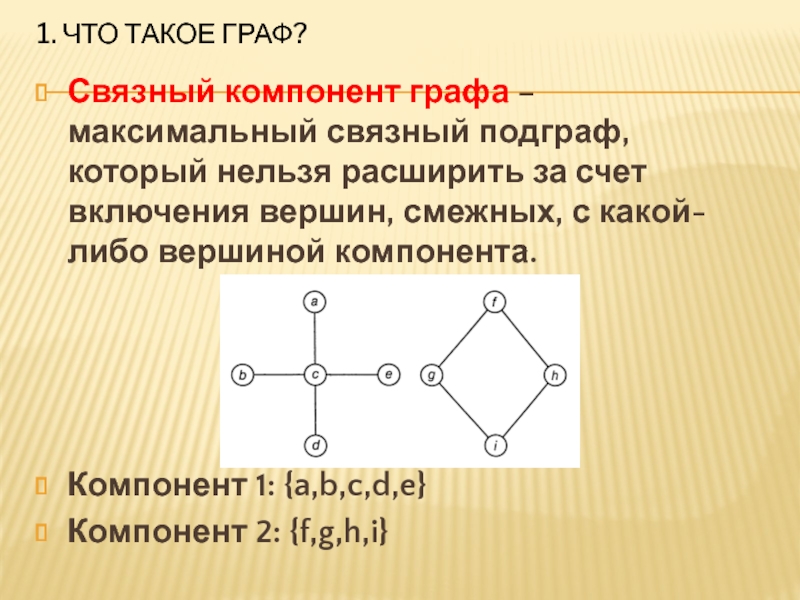
Связный компонент графа – максимальный связный подграф, который
нельзя расширить за счет включения вершин, смежных, с какой-либо вершиной компонента.
Компонент 1: {a,b,c,d,e}
Компонент 2: {f,g,h,i}
Компонент 1: {a,b,c,d,e}
Компонент 2: {f,g,h,i}
Слайд 191. Что такое граф?
Сильно связный граф – ориентированный граф, в котором
для любой пары вершин есть путь (не обязательно простой), который их соединяет.
Слайд 201. Что такое граф?
Сильно связный компонент графа – максимально связный подграф,
в котором любая вершина достижима из любой другой вершины.
Слайд 211. Что такое граф?
Плотный граф – граф, в котором количество ребер
близко к максимальному ((n2-n)/2)
Разреженный граф – граф, в котором количество ребер далеко от максимального.
Плотный Разреженный
Разреженный граф – граф, в котором количество ребер далеко от максимального.
Плотный Разреженный
Слайд 232. Как хранить графы?
Матрица смежности для графа с n вершинами состоит
из n*n элементов.
Строка – исходная вершина, столбец – входящая.
Если существует ребро, которое соединяет вершины a и b, тогда на пересечении строки a и столбца b ставится 1, если ребра нет – ставится 0.
Для неориентированного графа матрица смежности симметрична главной диагонали.
Строка – исходная вершина, столбец – входящая.
Если существует ребро, которое соединяет вершины a и b, тогда на пересечении строки a и столбца b ставится 1, если ребра нет – ставится 0.
Для неориентированного графа матрица смежности симметрична главной диагонали.
Слайд 242. Как хранить графы?
Списки смежности – массив связанных списков. Для n
вершин массив будет состоять из n элементов.
Каждый элемент массива – вершина, откуда выходит ребро.
Каждый элемент списка – вершина, в которую входит ребро.
Связный список формируется в произвольном порядке
Каждый элемент массива – вершина, откуда выходит ребро.
Каждый элемент списка – вершина, в которую входит ребро.
Связный список формируется в произвольном порядке
Слайд 252. Как хранить графы?
Для взвешенного графа
Матрица смежности представляет собой матрицу весов.
На пересечении a и b ставится вес ребра, или ∞, если ребра нет.
В связном списке появляется поле для обозначения веса ребра.
В связном списке появляется поле для обозначения веса ребра.
Слайд 262. Как хранить графы?
Выбор способа хранения графа зависит, как правило, от
используемых алгоритмов.
В остальных случаях, если граф плотный – лучше использовать матрицу смежности. Если граф разреженный – лучше использовать списки смежности.
В остальных случаях, если граф плотный – лучше использовать матрицу смежности. Если граф разреженный – лучше использовать списки смежности.