Смоленск 2014
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Алгоритмы на графах для МДК 01.02 Математический аппарат для построение компьютерных сетей
Содержание
- 1. Презентация по теме Алгоритмы на графах для МДК 01.02 Математический аппарат для построение компьютерных сетей
- 2. Поиск кратчайших путей в графеПоиск кратчайших путей из вершиныПоиск к.п. между всеми парами вершин
- 3. 1. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
- 4. 1. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕВарианты задачи
- 5. 1. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕОсновной принцип
- 6. 1. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕКратчайший путь
- 7. 1. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
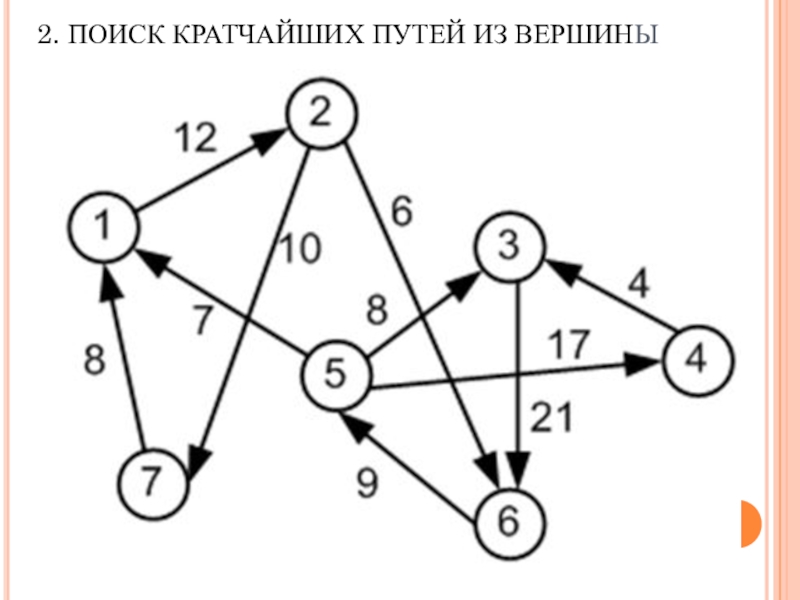
- 8. 2. ПОИСК КРАТЧАЙШИХ ПУТЕЙ ИЗ ВЕРШИНЫ
- 9. 2. ПОИСК КРАТЧАЙШИХ ПУТЕЙ ИЗ ВЕРШИНЫ
- 10. 2. ПОИСК КРАТЧАЙШИХ ПУТЕЙ ИЗ ВЕРШИНЫ
- 11. 3. ПОИСК К.П. МЕЖДУ ВСЕМИ ПАРАМИ ВЕРШИНПоиск
- 12. 3. ПОИСК К.П. МЕЖДУ ВСЕМИ ПАРАМИ ВЕРШИН
- 13. 3. ПОИСК К.П. МЕЖДУ ВСЕМИ ПАРАМИ ВЕРШИН
- 14. 3. ПОИСК К.П. МЕЖДУ ВСЕМИ ПАРАМИ ВЕРШИН
- 15. 3. ПОИСК К.П. МЕЖДУ ВСЕМИ ПАРАМИ ВЕРШИН
Поиск кратчайших путей в графеПоиск кратчайших путей из вершиныПоиск к.п. между всеми парами вершин
Слайд 1АЛГОРИТМЫ НА ГРАФАХ
МДК 01.02 Математический аппарат для построение компьютерных сетей
преподаватель Скряго
О.С.
Слайд 2Поиск кратчайших путей в графе
Поиск кратчайших путей из вершины
Поиск к.п. между
всеми парами вершин
Слайд 41. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
Варианты задачи поиска кратчайших путей:
Кратчайший путь
из вершины (из одной вершины во все остальные);
Кратчайший путь в заданную вершину (из всех остальных);
Кратчайший путь между заданной парой вершин (из заданной вершины в заданную);
Кратчайший путь между всем парами вершин (из всех во все).
Кратчайший путь в заданную вершину (из всех остальных);
Кратчайший путь между заданной парой вершин (из заданной вершины в заданную);
Кратчайший путь между всем парами вершин (из всех во все).
Слайд 51. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
Основной принцип алгоритмов поиска кратчайших путей:
кратчайший
путь между двумя вершинами содержит в себе другие кратчайшие пути
(кратчайшие пути к промежуточным вершинам).
(кратчайшие пути к промежуточным вершинам).
Слайд 61. ПОИСК КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
Кратчайший путь может содержать вершины с
отрицательным весом.
Если граф имеет цикл с отрицательным весом, который достижим из начальной вершины – алгоритмы могут работать неправильно.
Некоторые алгоритмы могут работать с отрицательными весами (Беллман-Форд), некоторые – нет (Дейкстра).
Если граф имеет цикл с отрицательным весом, который достижим из начальной вершины – алгоритмы могут работать неправильно.
Некоторые алгоритмы могут работать с отрицательными весами (Беллман-Форд), некоторые – нет (Дейкстра).
Слайд 113. ПОИСК К.П. МЕЖДУ ВСЕМИ ПАРАМИ ВЕРШИН
Поиск кратчайшего пути между всеми
парами вершин: поиск расстояний от каждой вершины до всех других вершин.
Для этого можно V раз выполнить алгоритм Дейкстры, но это вычислительно неоправдано.
Для этого можно V раз выполнить алгоритм Дейкстры, но это вычислительно неоправдано.