- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по системам счисления и арифметическим операциям.
Содержание
- 1. Презентация по системам счисления и арифметическим операциям.
- 2. Введение
- 3. Как это было? Счет появился тогда, когда человеку
- 4. ОпределенияСистема счисления – это способ записи чисел
- 5. Системы счисленияНепозиционная XXII VIIкаждой цифре соответствует
- 6. Непозиционные системы счисления
- 7. Римская (500 лет до н.э.)Натуральные числа
- 8. Где используется: номера глав в книгах: обозначение веков: «Пираты XX века» циферблат часов
- 9. Позиционные системы счисления
- 10. Позиционной называют систему счисления, в которой число
- 11. Системы счисления, используемые в компьютере
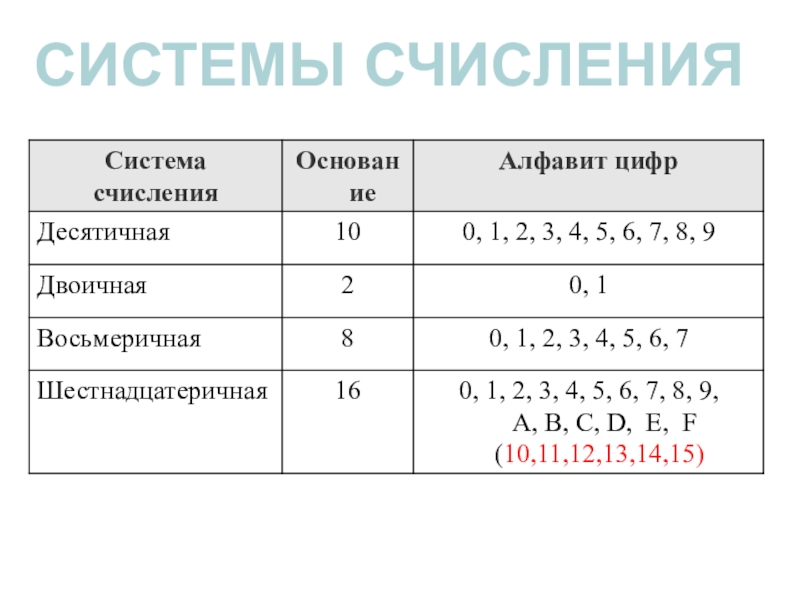
- 12. СИСТЕМЫ СЧИСЛЕНИЯ
- 13. Десятичная система счисления
- 14. Десятичная система счисленияДесятичная система: первоначально –
- 15. Двоичная система счисления
- 16. Перевод целых чиселДвоичная система: Алфавит: 0,
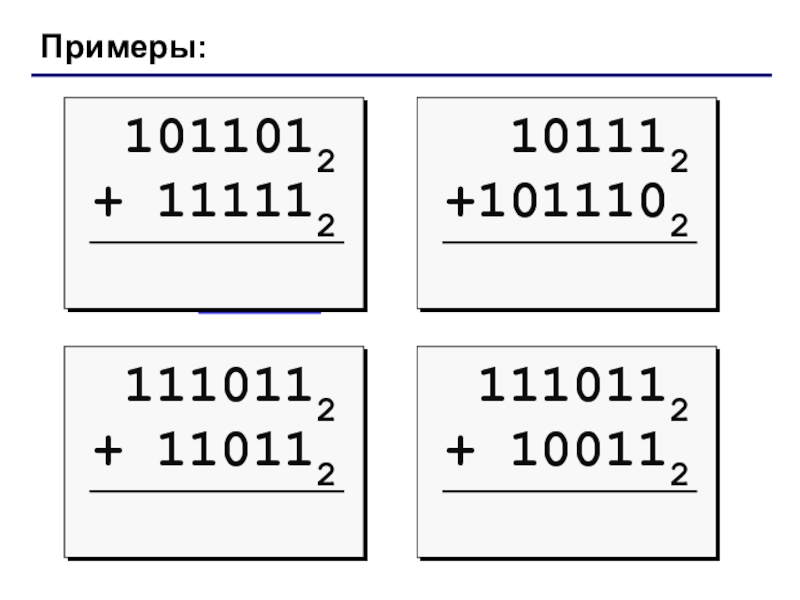
- 17. Примеры:131 =79 =
- 18. Примеры:1010112 =1101102 =
- 19. Восьмеричная система счисления
- 20. Восьмеричная системаОснование (количество цифр): 8Алфавит: 0, 1,
- 21. Примеры:134 =75 =1348 =758 =
- 22. Перевод в двоичную и обратно8102трудоемко2 действия8 =
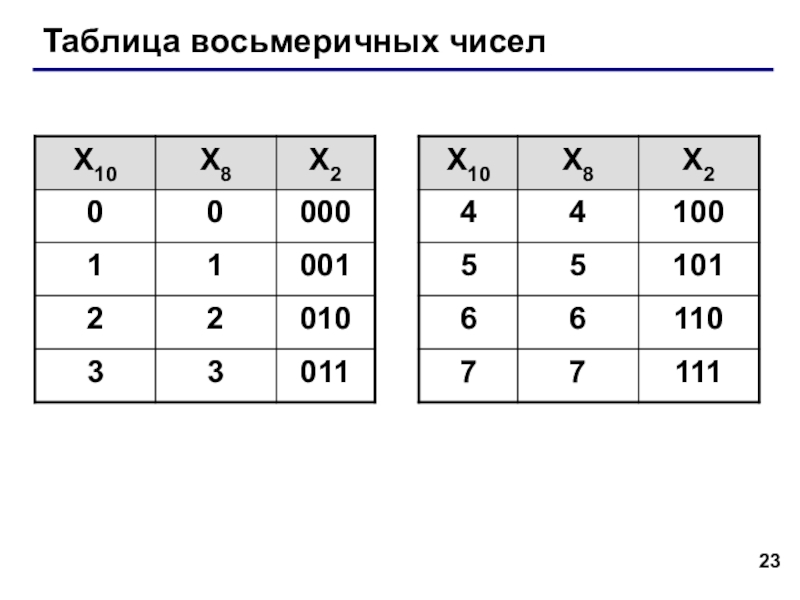
- 23. Таблица восьмеричных чисел
- 24. Перевод из двоичной системы10010111011112Шаг 1. Разбить на
- 25. Примеры:34678 =73528 =12318 =
- 26. Примеры:1011010100102 =111111010112 =11010110102 =
- 27. Шестнадцатеричная системы счисления
- 28. Шестнадцатеричная системаОснование (количество цифр): 16Алфавит: 0, 1,
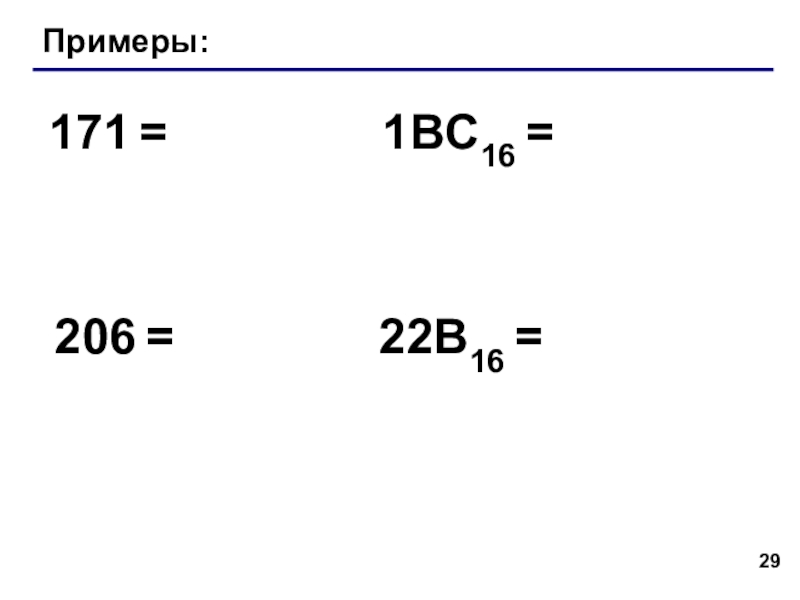
- 29. Примеры:171 =206 =1BC16 =22B16 =
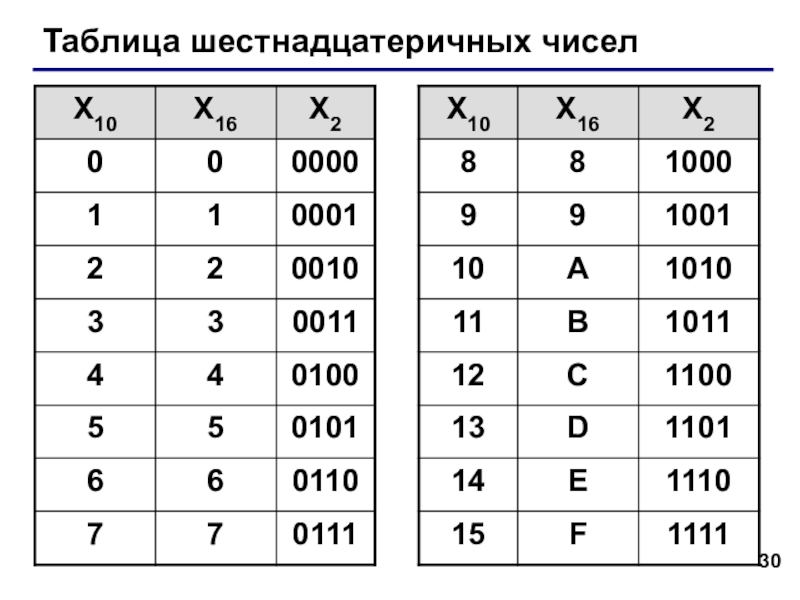
- 30. Таблица шестнадцатеричных чисел
- 31. Перевод в двоичную систему16102трудоемко2 действия16 = 247F1A16
- 32. Перевод из двоичной системы10010111011112Шаг 1. Разбить на
- 33. Примеры:C73B16 =2FE116 =
- 34. Примеры:10101011010101102 =1111001101111101012 =1101101101011111102 =
- 35. Перевод в восьмеричную и обратнотрудоемко3DEA16 = 11
- 36. Примеры:A3516 =7658 =
- 37. Перевод дробных чисел10 → 22 → 10
- 38. Арифметические операциисложениевычитание0+0=0 0+1=11+0=1 1+1=1021 + 1 +
- 39. 0 · 0 = 01 · 0
- 40. Арифметические операцииумножениеделение 1 0 1 0
Слайд 1Системы счисления
Введение
Непозиционная система счисления
Позиционная система счисления
Десятичная система
Двоичная система
Восьмеричная система
Шестнадцатеричная система
Слайд 3
Как это было?
Счет появился тогда, когда человеку потребовалось информировать своих сородичей
Слайд 4Определения
Система счисления – это способ записи чисел с помощью специальных знаков
Числа: 123, 45678, 1010011, CXL
Цифры: 0, 1, 2, … I, V, X, L, …
Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
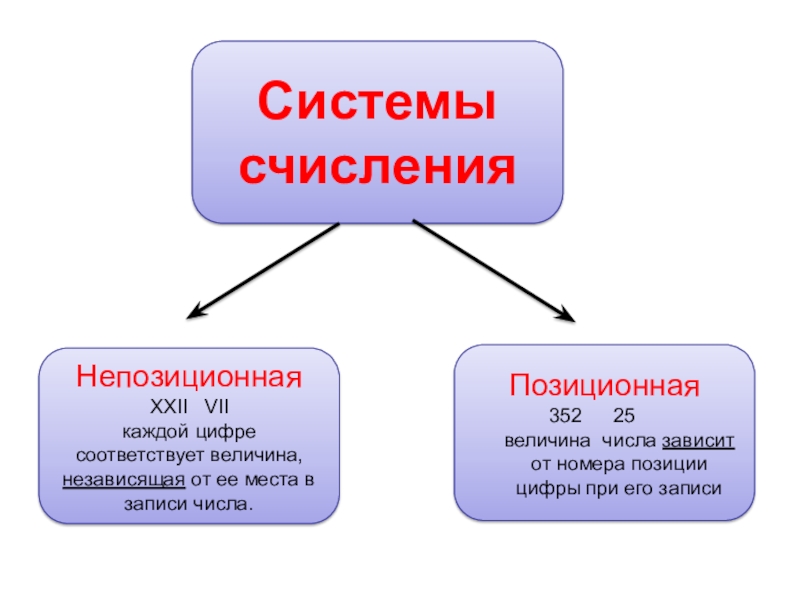
Слайд 5Системы счисления
Непозиционная
XXII VII
каждой цифре соответствует величина, независящая от ее
Позиционная
25 величина числа зависит от номера позиции цифры при его записи
Слайд 7Римская
(500 лет до н.э.)
Натуральные числа записываются при помощи повторения этих
Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе.
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.
MCMLXXXVIII = 1000+(1000-100)+(50+10+10+10)+5+1+1+1 = 1988
Для изображения чисел в непозиционной системе счисления нельзя ограничится конечным набором цифр. Кроме того, выполнение арифметических действий в них крайне неудобно.
Слайд 10Позиционной называют систему счисления, в которой число представляется в виде последовательности
3 3 3 3
1 позиция
* 1
2 позиция
* 10
3 пзиция
* 100
* 1000
1000 100 10 1
(103) (102) (101) (100)
Количество используемых цифр называется основанием системы счисления.
Например, 11 – это одиннадцать, а не два: 1 + 1 = 2 (сравните с римской системой счисления). Здесь символ 1 имеет различное значение в зависимости от позиции в числе.
Слайд 14Десятичная система счисления
Десятичная система:
первоначально – счет на пальцах
3 7 8
2
разряды
8
70
300
= 3·102 + 7·101 + 8·100
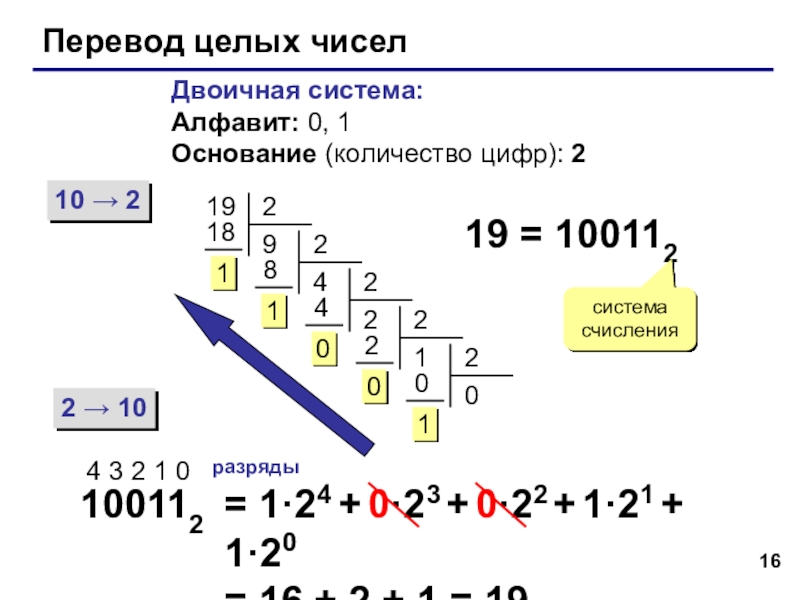
Слайд 16Перевод целых чисел
Двоичная система:
Алфавит: 0, 1
Основание (количество цифр): 2
10 →
2 → 10
19
19 = 100112
система счисления
100112
4 3 2 1 0
разряды
= 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
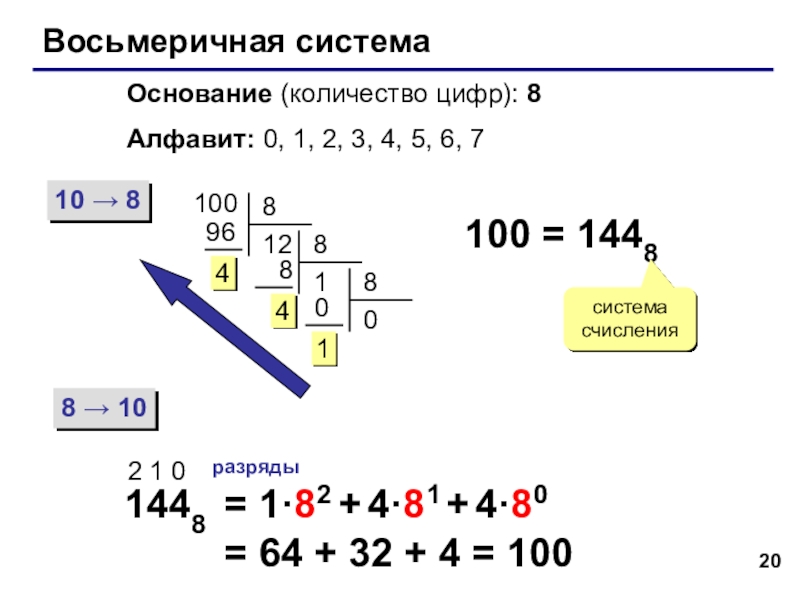
Слайд 20Восьмеричная система
Основание (количество цифр): 8
Алфавит: 0, 1, 2, 3, 4, 5,
10 → 8
8 → 10
100
100 = 1448
система счисления
1448
2 1 0
разряды
= 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
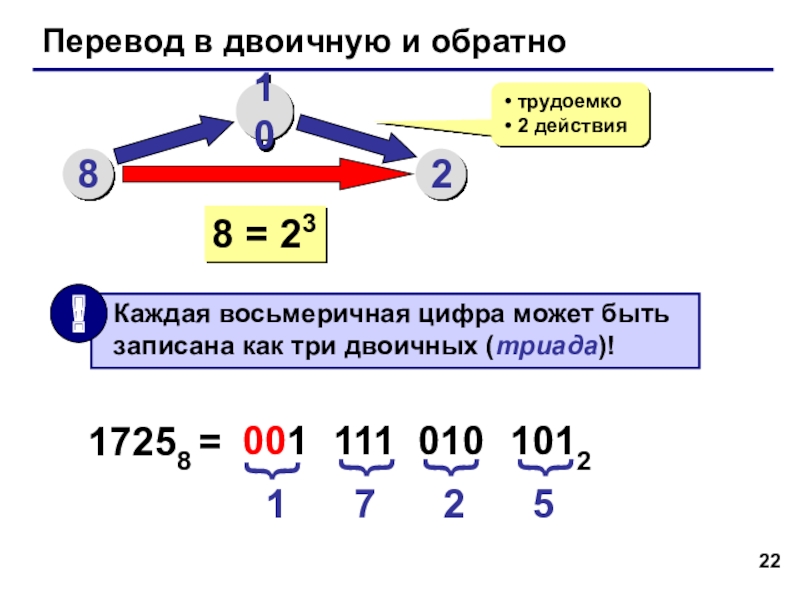
Слайд 22Перевод в двоичную и обратно
8
10
2
трудоемко
2 действия
8 = 23
17258 =
1
001
111
010
1012
{
{
{
{
Слайд 24Перевод из двоичной системы
10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
1
3
5
7
Ответ: 10010111011112 = 113578
001 001 011 101 1112
1
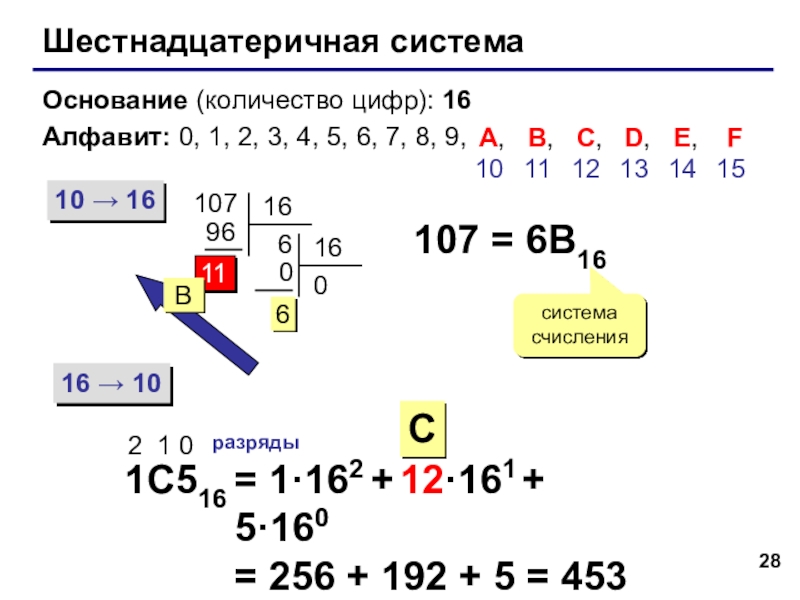
Слайд 28Шестнадцатеричная система
Основание (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5,
10 → 16
16 → 10
107
107 = 6B16
система счисления
1C516
2 1 0
разряды
= 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453
A,
10
B,
11
C,
12
D,
13
E,
14
F
15
B
C
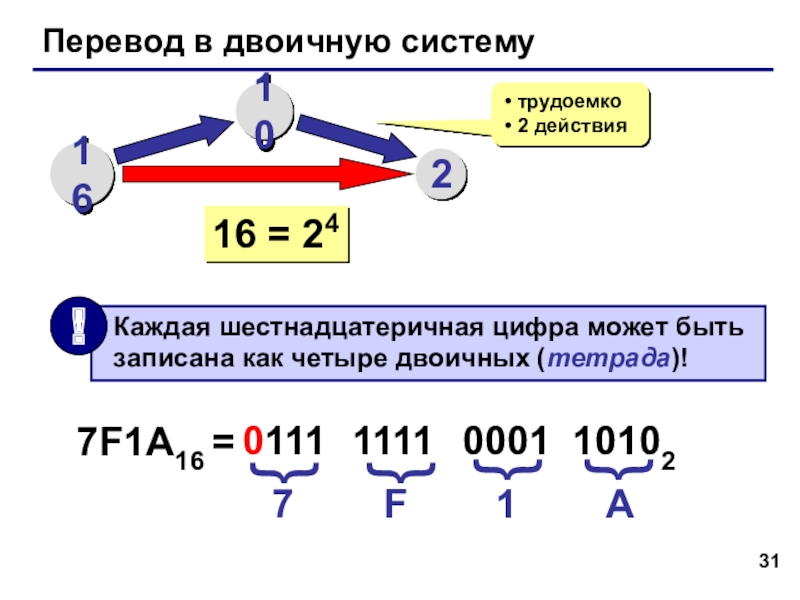
Слайд 31Перевод в двоичную систему
16
10
2
трудоемко
2 действия
16 = 24
7F1A16 =
7
0111
{
{
1111
0001
10102
{
{
Слайд 32Перевод из двоичной системы
10010111011112
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ: 10010111011112 = 12EF16
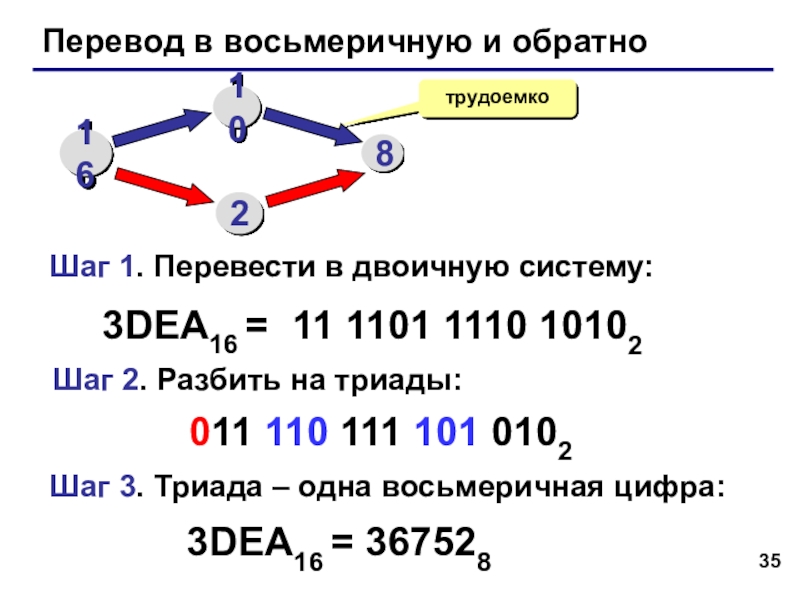
Слайд 35Перевод в восьмеричную и обратно
трудоемко
3DEA16 =
11 1101 1110 10102
16
10
8
2
Шаг 1.
Шаг 2. Разбить на триады:
Шаг 3. Триада – одна восьмеричная цифра:
011 110 111 101 0102
3DEA16 = 367528
Слайд 37Перевод дробных чисел
10 → 2
2 → 10
0,375 =
×
101,0112
2 1 0 -1 -2 -3
разряды
= 1·22 + 1·20 + 1·2-2 + 1·2-3
= 4 + 1 + 0,25 + 0,125 = 5,375
,750
0
0,75
× 2
,50
1
0,5
× 2
,0
1
0,7 = ?
0,7 = 0,101100110…
= 0,1(0110)2
Многие дробные числа нельзя представить в виде конечных двоичных дробей.
Для их точного хранения требуется бесконечное число разрядов.
Большинство дробных чисел хранится в памяти с ошибкой.
0,0112
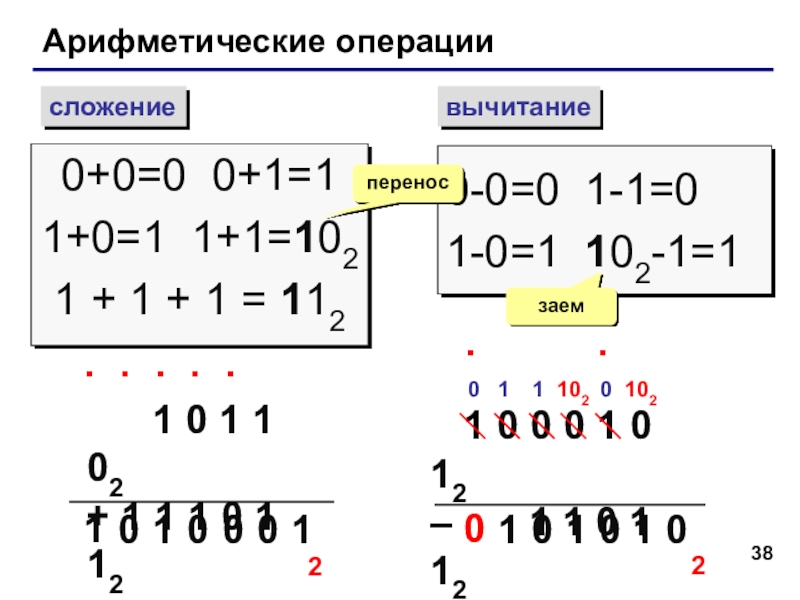
Слайд 38Арифметические операции
сложение
вычитание
0+0=0 0+1=1
1+0=1 1+1=102
1 + 1 + 1 = 112
0-0=0 1-1=0
1-0=1
перенос
заем
1 0 1 1 02
+ 1 1 1 0 1 12
1
∙
0
0
∙
0
1
1
0
2
1 0 0 0 1 0 12
– 1 1 0 1 12
1
∙
∙
0 102
1
0
0 1 1 102
0
1
0
∙
∙
∙
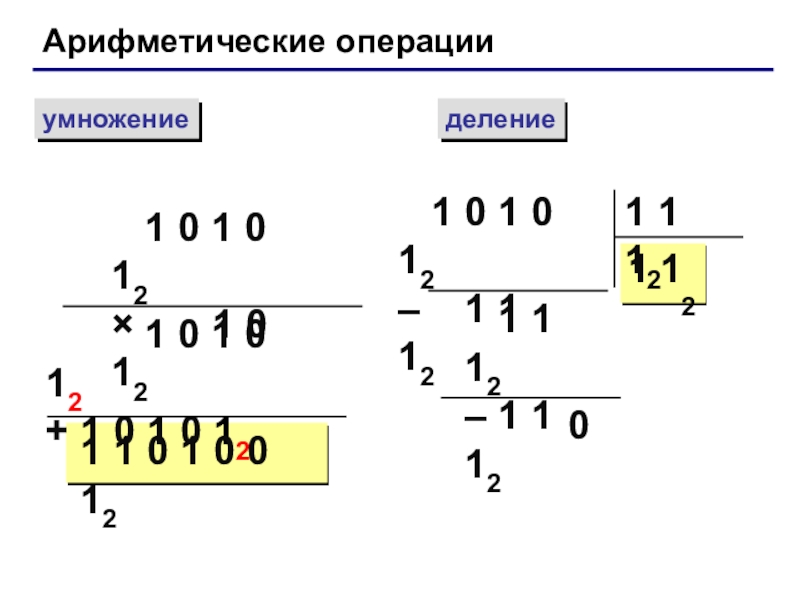
Слайд 40
Арифметические операции
умножение
деление
1 0 1 0 12
×
1 0 1 0 12
+ 1 0 1 0 12
1 1 0 1 0 0 12
1 0 1 0 12
– 1 1 12
1 1 12
1
1 1 12
– 1 1 12
0