- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Структуры данных: деревья, сети, графы, таблицы.
Содержание
- 1. Презентация по информатике Структуры данных: деревья, сети, графы, таблицы.
- 2. Объектом информационного моделирования может быть всё что
- 3. Рассмотрение множества объектов, объединенных единой целью функционирования позволяет говорить уже о системе.
- 4. Модель – это новый объект, который отражает
- 5. Слайд 5
- 6. Материальные модели иначе можно назвать предметными или
- 7. Данные, на которых базируются информационные модели, представляют
- 8. ГрафыОтображают элементный состав системы и структуру связей.Составные
- 9. Графы Пример 1, район состоит из пяти
- 10. Иерархические структуры (деревья) Элементы дерева:Корень дерева, вершины,
- 11. Иерархические структуры – деревья Основное свойство –
- 12. Династия РюриковичейРюрик 879Игорь945Святослав972Олег977Владимир1014Ярополк980МстиславТмутараканский1036Глеб1015Ярослав1054Борис1015Святополк1018ИзяславПолоцкий1001ИЕРАРХИЧЕСКАЯ МОДЕЛЬ
- 13. ТаблицыСтрокиСтолбцыЯчейкиТаблицы типа «объект – свойство»Каждая строка относится
- 14. ТаблицыЭлементы таблицы:Строки, столбцы, ячейкиТИПЫ ТАБЛИЦ«объект-свойство»«объект-объект»«объект-свойство»С помощью таблиц
- 15. «объект-объект»ТаблицыСвязь между объектами двух типов: учениками и
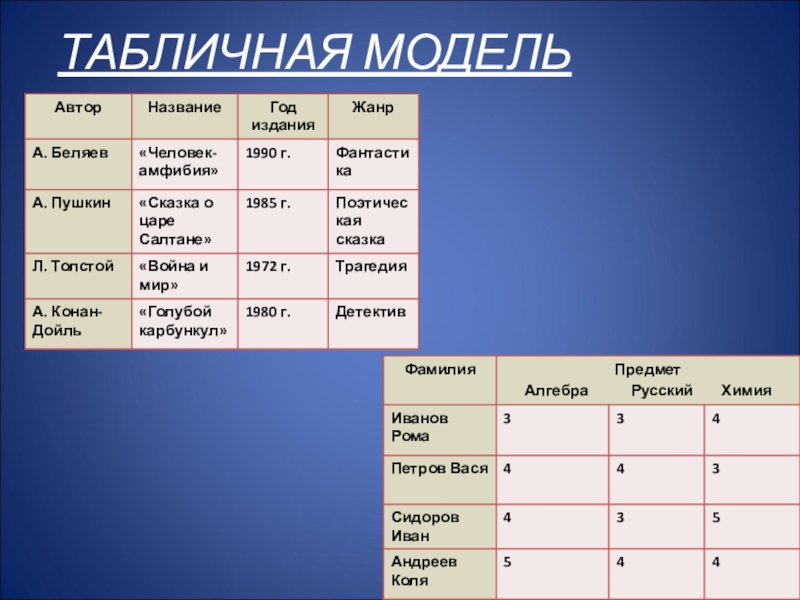
- 16. ТАБЛИЧНАЯ МОДЕЛЬ
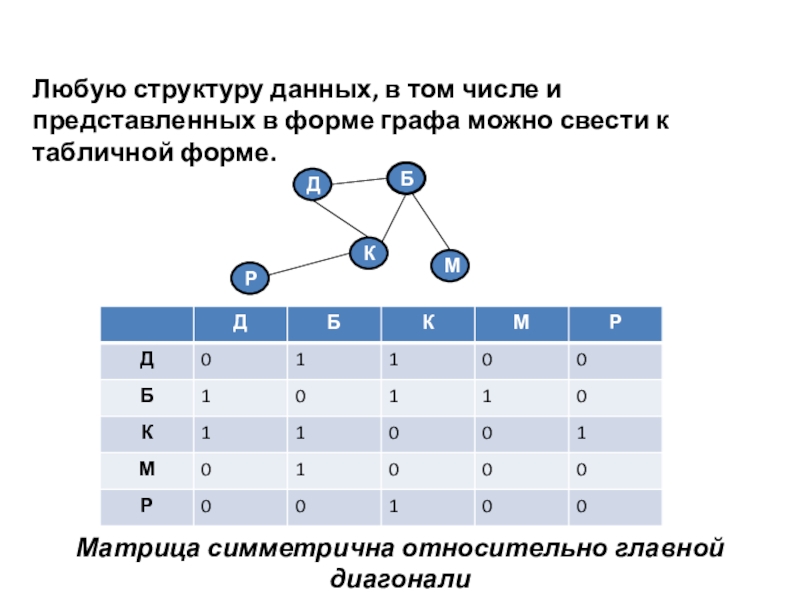
- 17. Любую структуру данных, в том числе и
- 18. Изобразите в виде графа систему, состоящую из
- 19. Двоичные матрицы удобно использовать для решения некоторых
- 20. Задания3. В школе учатся четыре талантливых мальчика:
- 21. Из условия задачи : Николаев НиколайСемёнов не
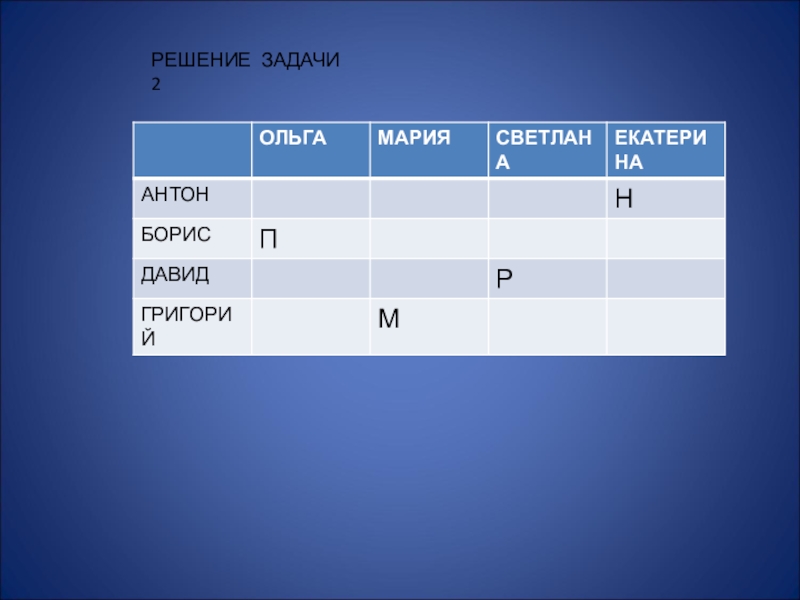
- 22. РЕШЕНИЕ ЗАДАЧИ 2
- 23. Решение задачи 3 1. Из первого пункта следует,
Слайд 2Объектом информационного моделирования может быть всё что угодно: отдельные предметы (дерево,
Слайд 3Рассмотрение множества объектов, объединенных единой целью функционирования позволяет говорить уже о
Слайд 4Модель – это новый объект, который отражает существенные с точки зрения
Моделирование – метод познания, заключающийся в создании и исследовании моделей.
Слайд 6Материальные модели иначе можно назвать предметными или физическими. Они воспроизводят геометрические
Примеры материальных моделей:
Детские игрушки (куклы – модель ребенка, машинки – модели реальных автомобилей и т.д.).
Глобус – модель планеты Земля.
Школьные пособия (скелет человека – модель реального скелета, модель атома кислорода и т.д.)
Физические и химические опыты.
Информационная модель – совокупность информации, характеризующая свойства и состояния объекта, процесса, явления, а также взаимосвязь с внешним миром.
Примеры моделей:
Чертеж кухонной мебели – модель мебели для кухни.
Схема Московского метрополитена – модель метро.
График изменения курса евро – модель роста курса евро.
По способу реализации информационные модели делятся на компьютерные и некомпьютерные.
Слайд 7Данные, на которых базируются информационные модели, представляют собой структурированные системы со
Их называют структурами данных.
По видам описания структур данных выделяют:
Графы
Иерархические структуры
Таблицы
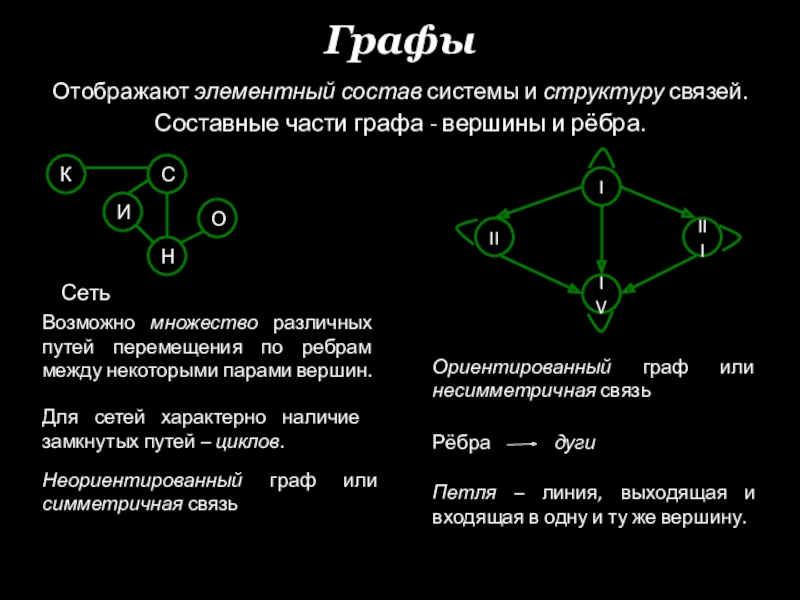
Слайд 8Графы
Отображают элементный состав системы и структуру связей.
Составные части графа - вершины
Сеть
Возможно множество различных путей перемещения по ребрам между некоторыми парами вершин.
Для сетей характерно наличие замкнутых путей – циклов.
Неориентированный граф или симметричная связь
Ориентированный граф или несимметричная связь
Рёбра дуги
Петля – линия, выходящая и входящая в одну и ту же вершину.
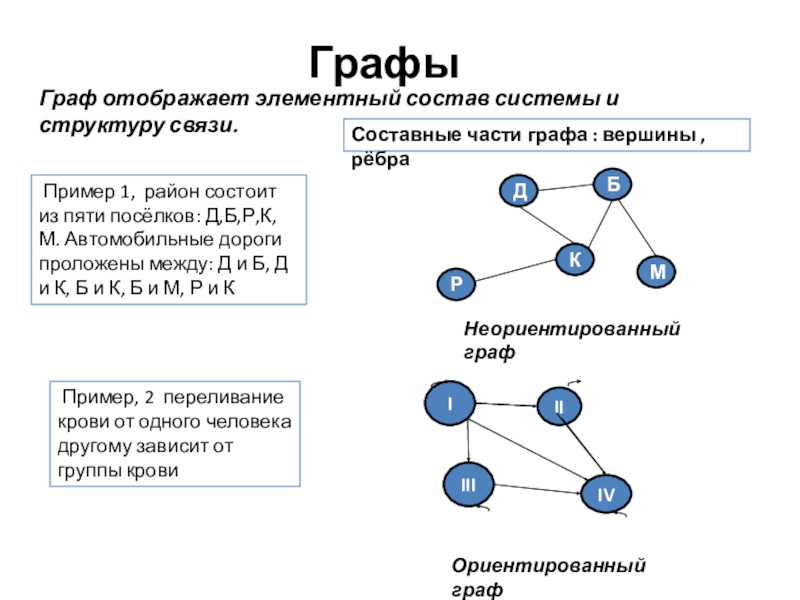
Слайд 9Графы
Пример 1, район состоит из пяти посёлков: Д,Б,Р,К, М. Автомобильные
Неориентированный граф
Граф отображает элементный состав системы и структуру связи.
Ориентированный граф
Пример, 2 переливание крови от одного человека другому зависит от группы крови
Составные части графа : вершины , рёбра
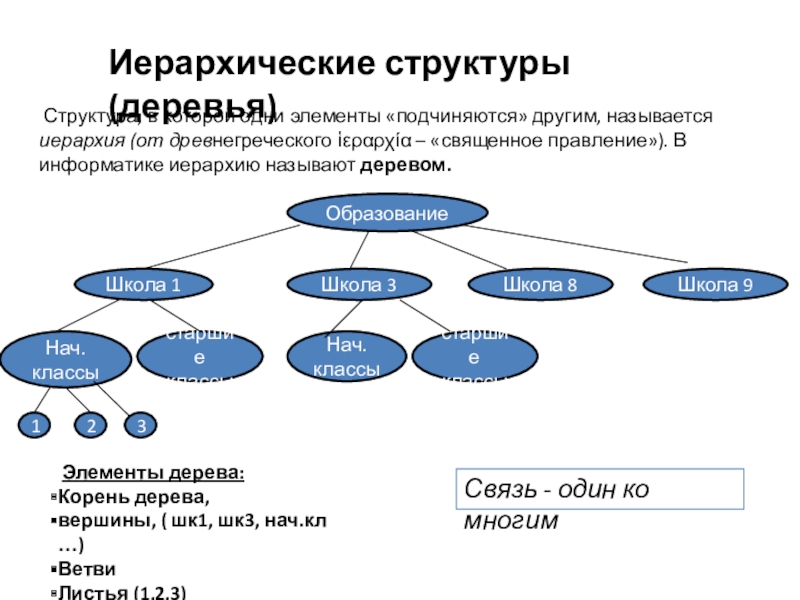
Слайд 10Иерархические структуры (деревья)
Элементы дерева:
Корень дерева,
вершины, ( шк1, шк3, нач.кл
Ветви
Листья (1,2,3)
Связь - один ко многим
Структура, в которой одни элементы «подчиняются» другим, называется иерархия (от древнегреческого ἱεραρχία – «священное правление»). В информатике иерархию называют деревом.
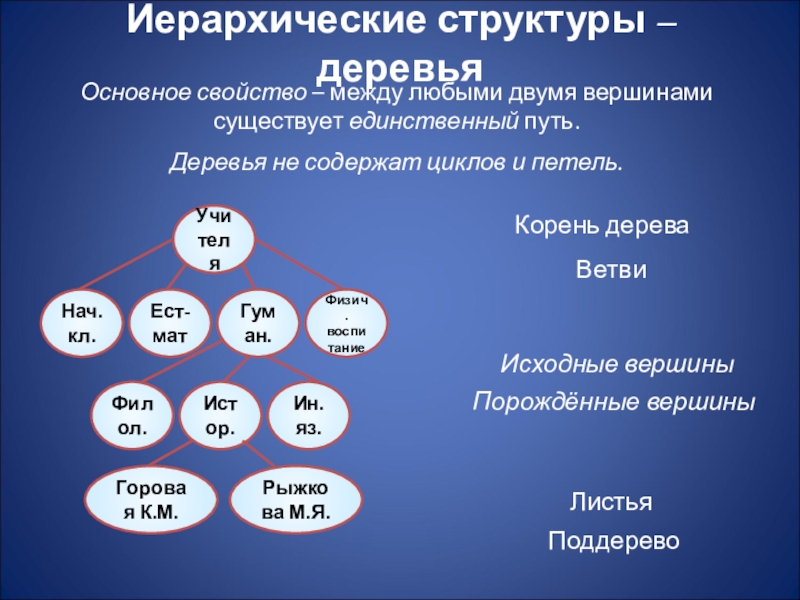
Слайд 11Иерархические структуры – деревья
Основное свойство – между любыми двумя вершинами
Деревья не содержат циклов и петель.
Корень дерева
Ветви
Исходные вершины
Порождённые вершины
Листья
Поддерево
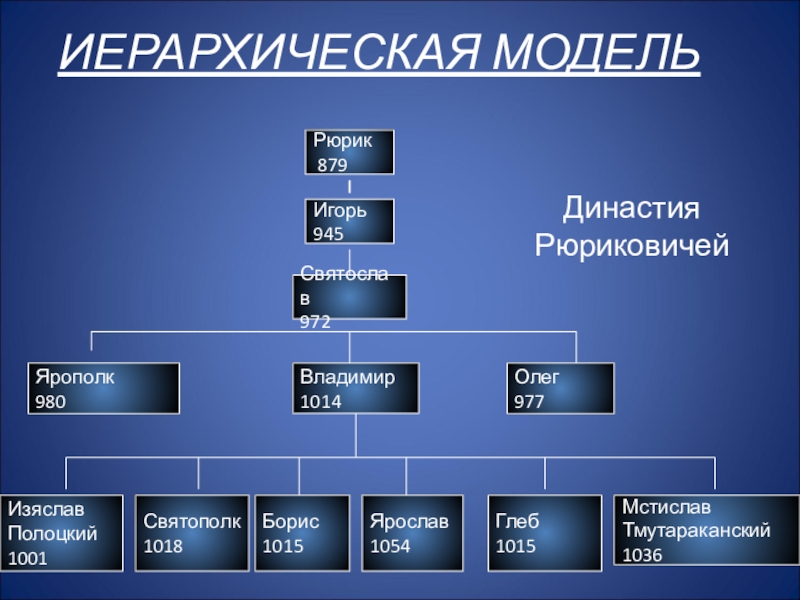
Слайд 12Династия Рюриковичей
Рюрик
879
Игорь
945
Святослав
972
Олег
977
Владимир
1014
Ярополк
980
Мстислав
Тмутараканский
1036
Глеб
1015
Ярослав
1054
Борис
1015
Святополк
1018
Изяслав
Полоцкий
1001
ИЕРАРХИЧЕСКАЯ МОДЕЛЬ
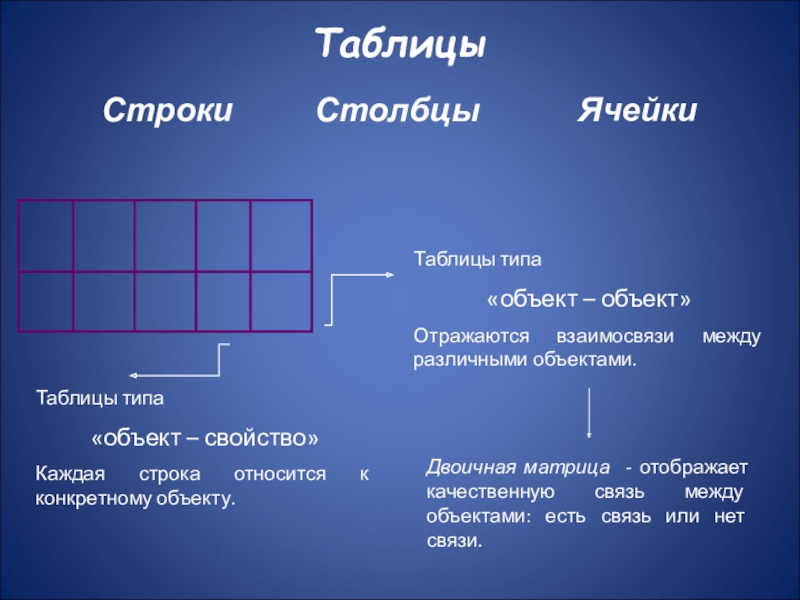
Слайд 13Таблицы
Строки
Столбцы
Ячейки
Таблицы типа
«объект – свойство»
Каждая строка относится к конкретному объекту.
Таблицы типа
«объект – объект»
Отражаются взаимосвязи между различными объектами.
Двоичная матрица - отображает качественную связь между объектами: есть связь или нет связи.
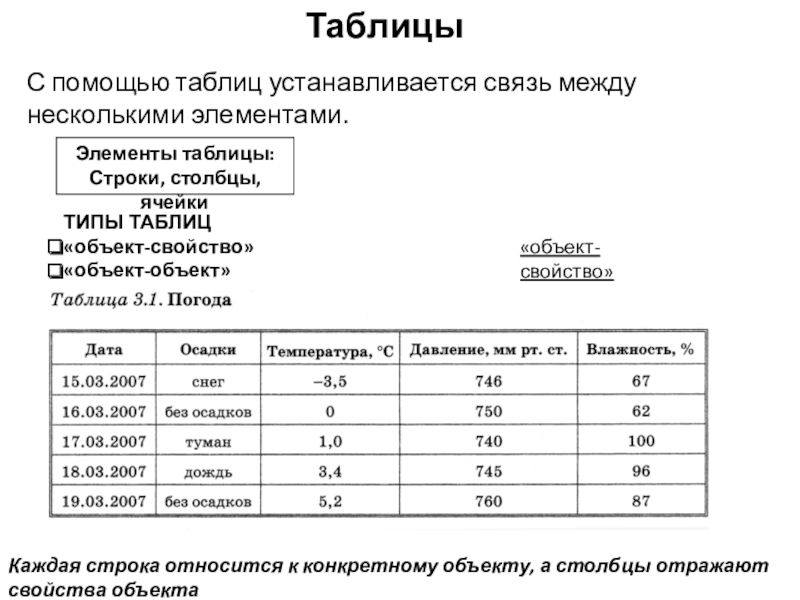
Слайд 14Таблицы
Элементы таблицы:
Строки, столбцы, ячейки
ТИПЫ ТАБЛИЦ
«объект-свойство»
«объект-объект»
«объект-свойство»
С помощью таблиц устанавливается связь между несколькими
Каждая строка относится к конкретному объекту, а столбцы отражают свойства объекта
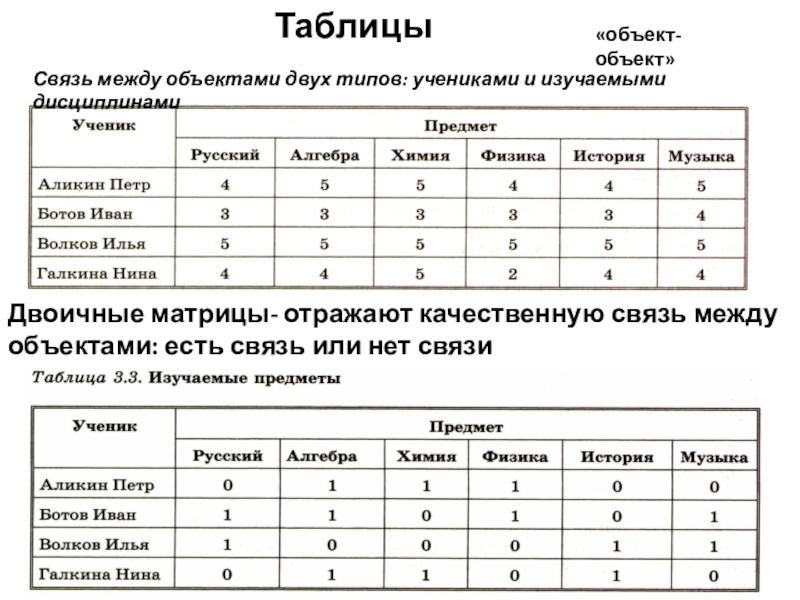
Слайд 15«объект-объект»
Таблицы
Связь между объектами двух типов: учениками и изучаемыми дисциплинами
Двоичные матрицы- отражают
Слайд 17Любую структуру данных, в том числе и представленных в форме графа
Матрица симметрична относительно главной диагонали
для неориентированного графа
Слайд 18Изобразите в виде графа систему, состоящую из четырех одноклассников, между которыми
Нарисовать ориентированный граф (блок-схему) проверки учителем тетрадей. В систему команд входят команды : проверить работу; взять тетрадь из пачки; выставить оценку; выяснить, остались ли ещё не проверенные тетради.
Нарисуйте два варианта графа системы «Компьютер», содержащего следующие вершины: процессор, оперативная память, внешняя память, клавиатура, монитор, принтер; а) линия связи обозначает отношение «передает информацию»; б) линия связи обозначает отношение «управляет».
Нарисуйте блок-схему поиска фальшивой монеты среди 10 монет. Имеем чашечные весы и известно, что фальшивая монета всего одна , и она легче настоящих.
Задания
Слайд 19Двоичные матрицы удобно использовать для решения некоторых логических задач — головоломок.
Имена Иванова, Петрова, Семенова и Николаева — Иван, Петр, Семен и Николай, причем только у Николаева имя совпадает с фамилией, т. е. его зовут Николай. Семенова зовут не Петром. Определить фамилию и имя каждого человека.
В Норильске, Москве, Ростове и Пятигорске живут четыре супружеские пары, причем в каждом городе — только одна пара. Имена этих супругов: Антон, Борис, Давид, Григорий, Ольга, Мария, Светлана, Екатерина. Антон живет в Норильске, Борис и Ольга — супруги, Григорий и Светлана не живут в одном городе, Мария живет в Москве, Светлана — ростовчанка. Кто на ком женат и кто где живет?
Задания
Слайд 20Задания
3. В школе учатся четыре талантливых мальчика: Иванов, Петров, Сидоров и
О них известно следующее:
Иванов и Сидоров присутствовали в зале консерватории, когда там солировал в хоре мальчиков певец.
Петров и музыкант вместе позировали художнику.
Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться с Ивановым.
Иванов не знаком с Сидоровым, так как они учатся в разных классах и в разные смены.
Кто чем увлекается?
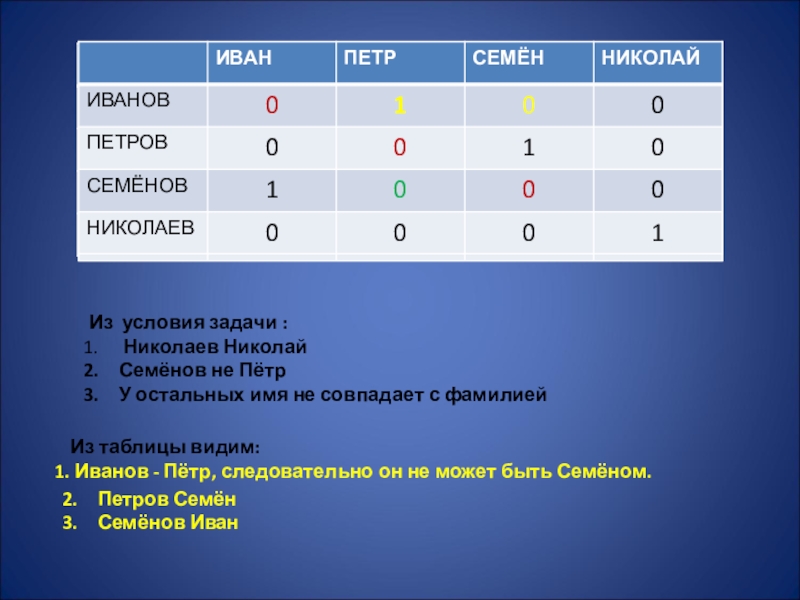
Слайд 21Из условия задачи :
Николаев Николай
Семёнов не Пётр
У остальных имя не
Из таблицы видим:
Иванов - Пётр, следовательно он не может быть Семёном.
Петров Семён
Семёнов Иван
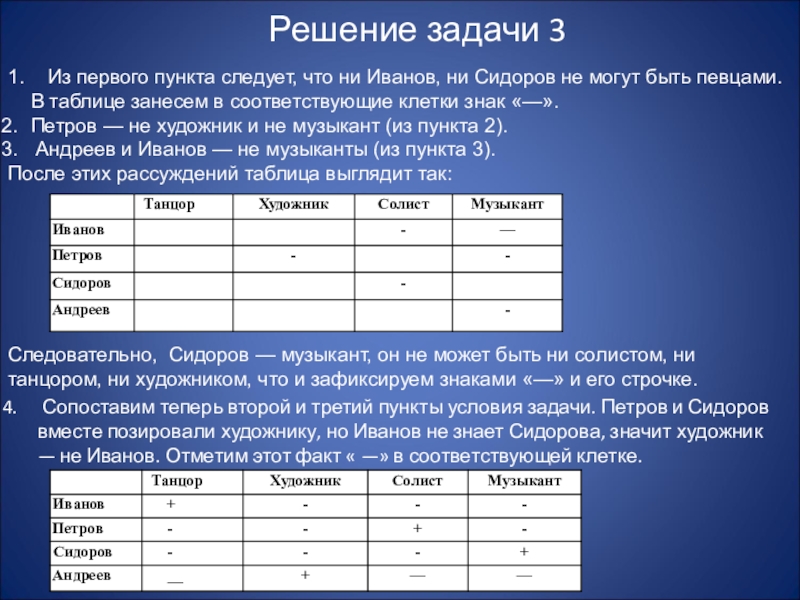
Слайд 23Решение задачи 3
1. Из первого пункта следует, что ни Иванов, ни
Петров — не художник и не музыкант (из пункта 2).
Андреев и Иванов — не музыканты (из пункта 3).
После этих рассуждений таблица выглядит так:
Следовательно, Сидоров — музыкант, он не может быть ни солистом, ни танцором, ни художником, что и зафиксируем знаками «—» и его строчке.
Сопоставим теперь второй и третий пункты условия задачи. Петров и Сидоров вместе позировали художнику, но Иванов не знает Сидорова, значит художник — не Иванов. Отметим этот факт « —» в соответствующей клетке.