- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Системы счисления, 8 класс
Содержание
- 1. Презентация по информатике Системы счисления, 8 класс
- 2. Содержание:Двоичное кодирование в ПКЧто такое система счисления?Непозиционные
- 3. Двоичное кодирование в компьютереВся информация, которую обрабатывает
- 4. С помощью двух цифр 0 и 1
- 5. Система счисления Почему мы используем цифры от
- 6. Виды систем счисленияСИСТЕМЫ СЧИСЛЕНИЯПОЗИЦИОННЫЕНЕПОЗИЦИОННЫЕВ непозиционных системах счисления
- 7. Непозиционные системы счисленияЯрким примером фактически непозиционной системы
- 8. Первые позиционные системы счисленияСамой первой такой системой,
- 9. Следующая позиционная система счисления была придумана еще
- 10. Десятичная система счисления Десятичная система счисления —
- 11. Двоичная система счисления Двоичная система счисления —
- 12. Алфавит двоичной, восьмеричной, десятичной и шестнадцатеричной систем счисленияКоличество используемых цифр называется основанием системы счисления.
- 13. Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем
- 14. Перевод чисел из любой позиционной системы счисления
- 15. Перевод целых десятичных чисел в 2, 8, 16-ую системы счисления
- 16. Перевод чисел из десятичной системы счисления в
- 17. Перевести десятичное число 26 в двоичную, троичную,
- 18. Перевести десятичную дробь 0,3750 375*
- 19. Переведи в 2-ую СС26,37510→Х22610=1101020,37510=0,011226,37510=11010,0112
- 20. Прочитайте стихотворение. Переведите встречающиеся в нем числительные
- 21. Задания:Запишите число в римской системе счисления:2013=Запишите в
- 22. Перевод 2 ↔ 8 СС Очень просто! Направо
- 23. Системы счисления, используемые в ЭВМ (с
- 24. Перевод 2 ↔ 16 СС Очень
- 25. Перевести число 11001010011010101112 в шестнадцатеричную систему счисления
- 26. Перевести число из восьмеричной системы счисления в шестнадцатеричную14515278 Х16меню
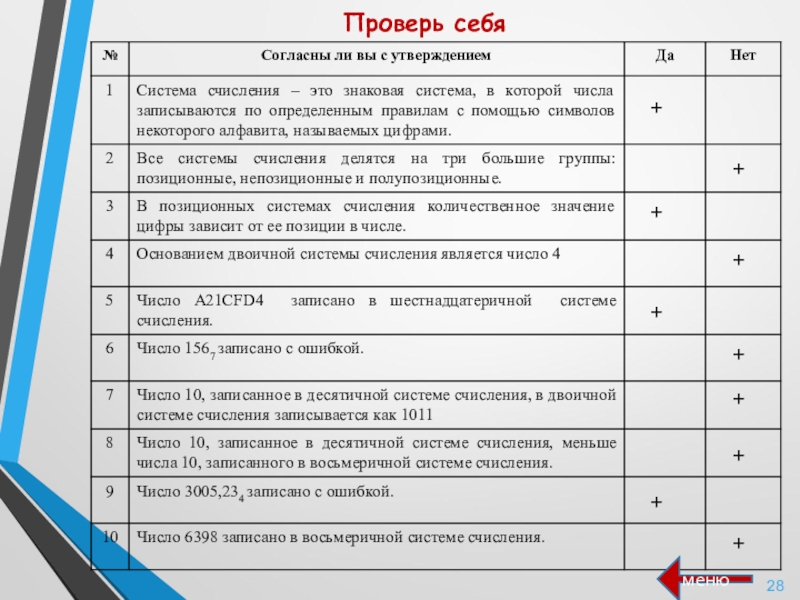
- 27. Согласны ли Вы с утверждениями….?
- 28. Проверь себя++++++++++меню
- 29. «Арифметические операции в позиционных системах счисления»
- 30. Все позиционные системы счисления «одинаковы», а именно,
- 31. Сложение в двоичной системе счисления: 0+0=0
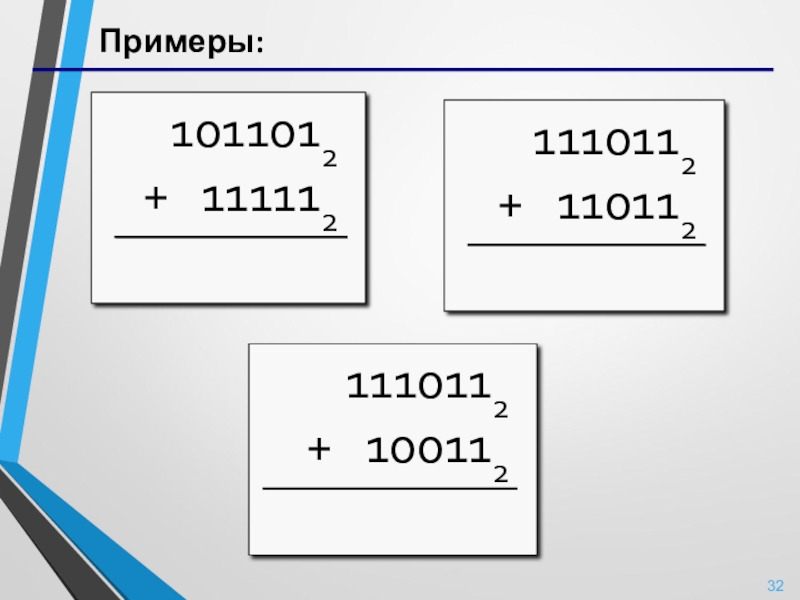
- 32. Примеры:
- 33. Вычитание в двоичной системе счисления:0-0=0
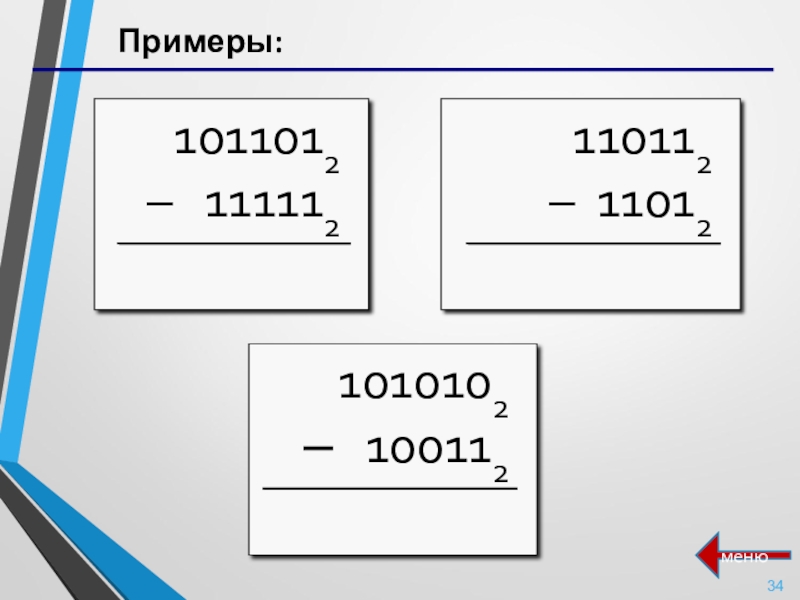
- 34. Примеры:меню
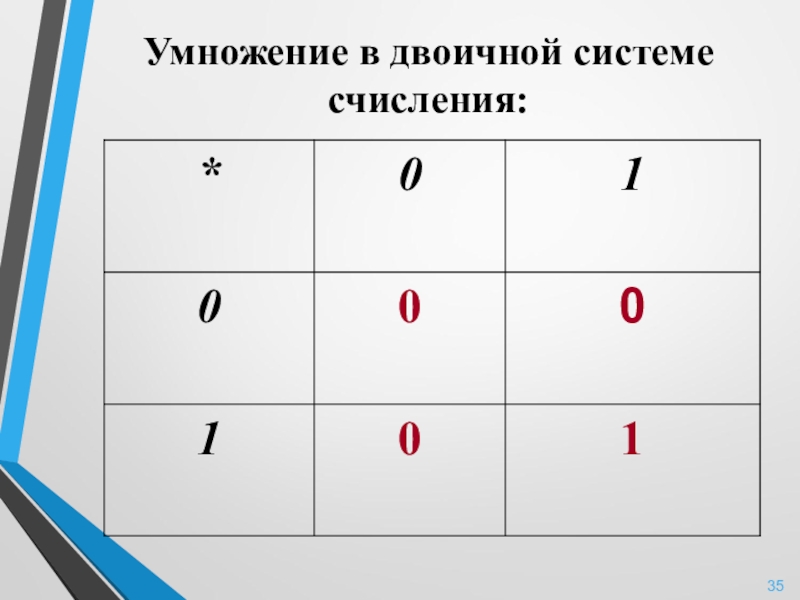
- 35. Умножение в двоичной системе счисления:
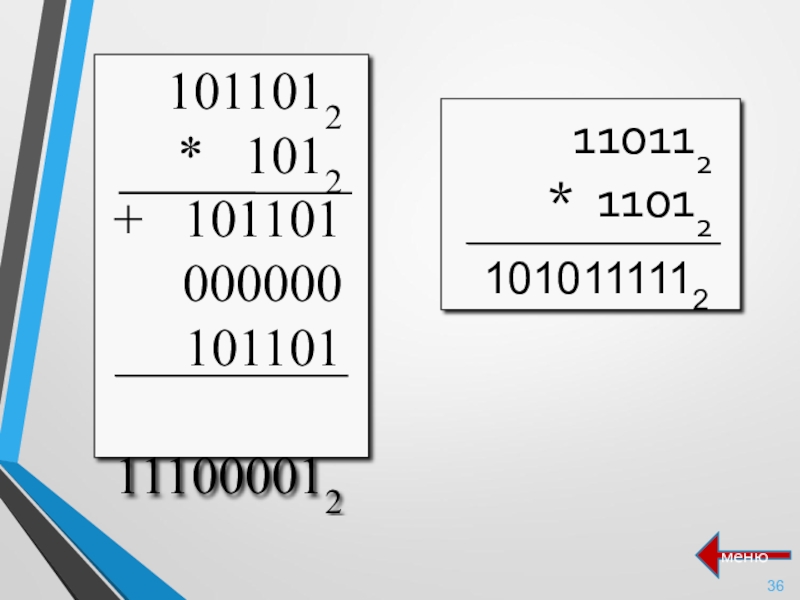
- 36. 1010111112меню
- 37. Арифметические операции в 8-ричной ССсложение1 5 68
- 38. Пример
- 39. Арифметические операции в 8-ричной ССвычитание2 1 5
- 40. Примерыменю
- 41. Решение примеров
- 42. Задание №1 1. Переведите числа данные в десятичной
- 43. ОТВЕТ на задание №11. 143,2510
- 44. Задание №2Переведите в восьмеричную и шестнадцатеричную СС:110010,1012 1011010011,0121101111011,012 101000010,01112
- 45. ОТВЕТ на задание № 2110010,1012=62,58=32,А161011010011,012=1323,28=2D3,4161101111011,012=1573,28=37B,416101000010,01112=502,348=142,716
- 46. Задание №31. Сложите данные числа:110011001,00112+ 111011101,010122. Выполните вычитание:1101100110,012 – 110000010,101123.Выполните умножение:10011112 х 10001002
- 47. Ответ на задание №3 1. 110 011
- 48. Задание №4 1. Переведите число данное в десятичной
- 49. ОТВЕТ на задание №41. 67010
- 50. Восстановить неизвестные цифры, обозначенные *, определив вначале
Слайд 2Содержание:
Двоичное кодирование в ПК
Что такое система счисления?
Непозиционные системы счисления
Позиционные системы счисления
Перевод
Перевод из 10-тичной СС
Перевод из 2-ной в 8-ную и обратно
Перевод из 2-ной в 16-ную и обратно
Опрос
Арифметические операции в позиционных СС
Сложение и вычитание в 2-ой СС
Умножение в 2-ой СС
Сложение и вычитание в 8-ой СС
Решение примеров
Слайд 3Двоичное кодирование в компьютере
Вся информация, которую обрабатывает компьютер должна быть представлена
С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов.
Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.
0 – отсутствие электрического сигнала;
1 – наличие электрического сигнала.
Слайд 4С помощью двух цифр 0 и 1 можно закодировать любое сообщение.
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.
меню
Слайд 5Система счисления
Почему мы используем цифры от 0 до 9? А
Система счисления (СС) — способ записи чисел с помощью набора специальных знаков, называемых цифрами.
меню
Слайд 6Виды систем счисления
СИСТЕМЫ СЧИСЛЕНИЯ
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
В непозиционных системах счисления величина, которую обозначает цифра,
XXI
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции).
211
Слайд 7Непозиционные системы счисления
Ярким примером фактически непозиционной системы счисления является римская, в
I обозначает 1, V - 5, X - 10, L - 50, C - 100, D - 500, M -1000.
Натуральные числа записываются при помощи повторения этих цифр. Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе.
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Пример: число 1789. Одна тысяча M, семь сотен DCC, восемьдесят LXXX, девять IX. Запишем их вместе: MDCCLXXXIX.
MDCCLXXXIX=1000+(500+100+100)+(50+10+10+10)+(10-1)=1789
Для изображения чисел в непозиционной системе счисления нельзя ограничится конечным набором цифр. Кроме того, выполнение арифметических действий в них крайне неудобно.
меню
Слайд 8Первые позиционные системы счисления
Самой первой такой системой, когда счетным "прибором" служили
Следующей возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Возможно, что она возникала у них из подсчёта фаланг на руке большим пальцем.
На ее широкое использование в прошлом указывает сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов.
Элементом двенадцатеричной системы в современности может служить счёт дюжинами.
Английский фунт состоит из 12 шиллингов.
Слайд 9Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем
В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
Слайд 10Десятичная система счисления
Десятичная система счисления — позиционная система счисления по
Предполагается, что основание 10 связано с количеством пальцев на руках у человека.
Наиболее распространённая система счисления в мире.
Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Слайд 11Двоичная система счисления
Двоичная система счисления — позиционная система счисления с
Используются цифры 0 и 1.
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям:
Чем меньше значений существует в системе, тем проще изготовить отдельные элементы.
Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.
Простота создания таблиц сложения и умножения — основных действий над числами
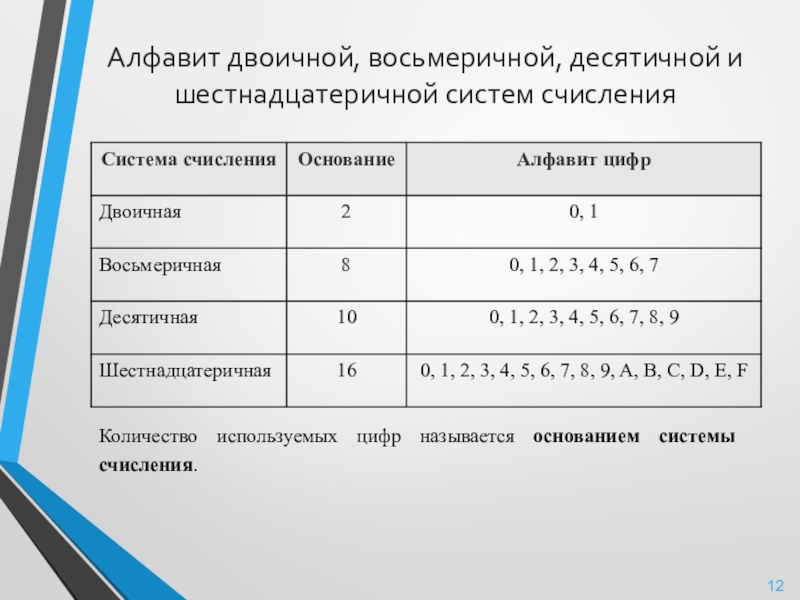
Слайд 12Алфавит двоичной, восьмеричной, десятичной и шестнадцатеричной систем счисления
Количество используемых цифр называется
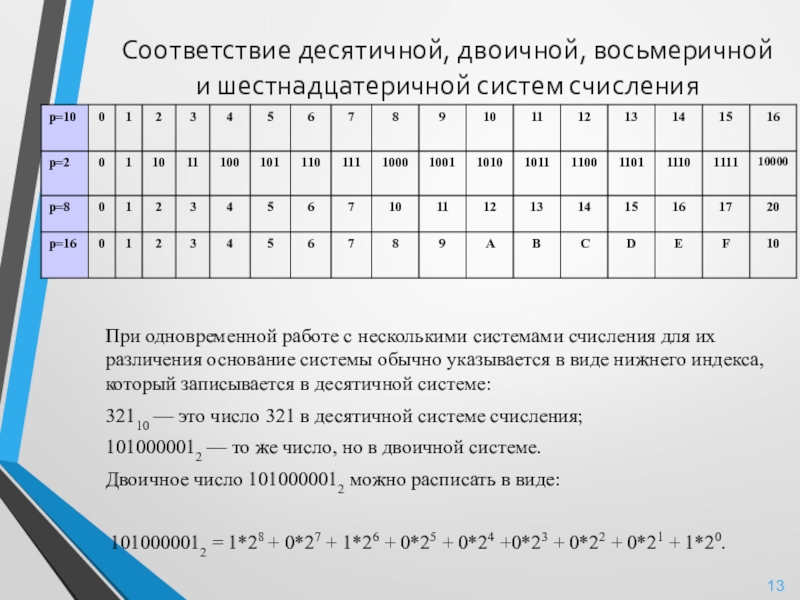
Слайд 13Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
При одновременной работе с
32110 — это число 321 в десятичной системе счисления;
1010000012 — то же число, но в двоичной системе.
Двоичное число 1010000012 можно расписать в виде:
1010000012 = 1*28 + 0*27 + 1*26 + 0*25 + 0*24 +0*23 + 0*22 + 0*21 + 1*20.
Слайд 14Перевод чисел из любой позиционной системы счисления в десятичную
Чтобы перевести целое
Например, переведем число 110012 в десятичную систему счисления. Для этого представим это число в виде степеней двойки и произведем вычисления в десятичной системе счисления.
110012 = 1*24 + 1*23 + 0*22 + 0*21 + 1*20 = 1*16 +1*8 + 0*4 + 0*2 + 1*1 = 16 + 8 + 0 + 0 + 1 = 2510
Рассмотрим еще один пример. Переведем число 12,348 в десятичную систему счисления.
12,348 = 1*81 + 2*80 + 3*8-1 + 4*8-2 = 1*8 + 2*1 + 3*1/8 +4*1/64 = 10 + 0,375 + 0,0625 = 10,437510
0
1
2
3
4
0
1
-1
-2
меню
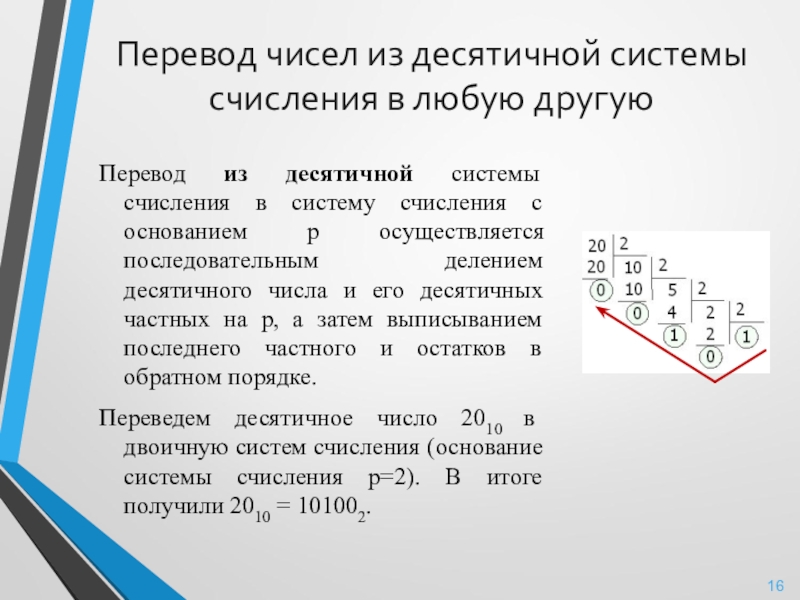
Слайд 16Перевод чисел из десятичной системы счисления в любую другую
Перевод из десятичной
Переведем десятичное число 2010 в двоичную систем счисления (основание системы счисления p=2). В итоге получили 2010 = 101002.
Слайд 17Перевести десятичное число 26 в двоичную, троичную, шестнадцатеричную системы
2610→Х2
26
13 1
6 0
3 1
1 1
2610=110102
2610→Х3
26 2
8 2
2 2
2610=2223
2610→Х16
26 10
1 1
2610=1А16
ПЕРЕВОД ЦЕЛОГО ДЕСЯТИЧНОГО ЧИСЛА МЕТОДОМ ПОЭТАПНОГО ДЕЛЕНИЯ
Слайд 18Перевести десятичную дробь 0,375
0 375
* 2
0 750
1 500
2
1 000
0,37510=0,0112
0 375
* 3
1 125
3
0 375
3
1 125
0,37510=0,1013
0 375
16
2 250
3 75
6 000
0,37510=0,616
Слайд 20Прочитайте стихотворение. Переведите встречающиеся в нем числительные из двоичной системы счисления
Необыкновенная девчонка
(А. Н. Стариков)
Ей было тысяча сто лет,
Она в 101-ый класс ходила,
В портфеле по сто книг носила –
Все это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз
Рассматривали мир привычно,…
Но станет все совсем обычным,
Когда поймете наш рассказ.
Слайд 21Задания:
Запишите число в римской системе счисления:
2013=
Запишите в развернутом виде числа:
123410
3458 =
110102 =
Переведите числа в десятичную систему счисления:
2748 =
BE16=
110,1012=
Как будет записываться число 2410 в двоичной системе счисления? 12310 в восьмеричной?
меню
Слайд 22Перевод 2 ↔ 8 СС
Очень просто! Направо и налево от точки
Пример:
1011010,011012 = 001 011 010,011 0102 = 132,328
Обратно - с точностью до наоборот:
257,318 = 010 101 111, 011 0012 = 10101111,0110012
Слайд 23Системы счисления, используемые в ЭВМ
(с основанием 2n)
Перевести число 11001010011010101112
в восьмеричную систему счисления
001 100 101 001 101 010 111
1 4 5 1 5 2 7
Получаем 14515278
меню
Слайд 24Перевод 2 ↔ 16 СС
Очень просто! Направо и налево
Пример:
1011010110,0110012 = 0010 11 01 0110,011 0102 = 132,328
Обратно - с точностью до наоборот:
257,318 = 010 101 111, 011 0012 = 10101111,0110012
Слайд 25Перевести число 11001010011010101112
в шестнадцатеричную систему счисления
0110 0101
6 5 3 5 7
Получаем 6535716
Слайд 30Все позиционные системы счисления «одинаковы», а именно, во всех них выполняются
справедливы одни и те же законы арифметики:
-коммутативный (переместительный): m + n = n + m
m · n = n · m
ассоциативный (сочетательный): (m + n) + k = m + (n + k) = m + n + k
(m · n) · k = m · (n · k) = m · n · k
дистрибутивный (распределительный): (m + n) · k = m · k + n · k
справедливы правила сложения, вычитания и умножения столбиком;
правила выполнения арифметических операций опираются на таблицы сложения и умножения.
меню
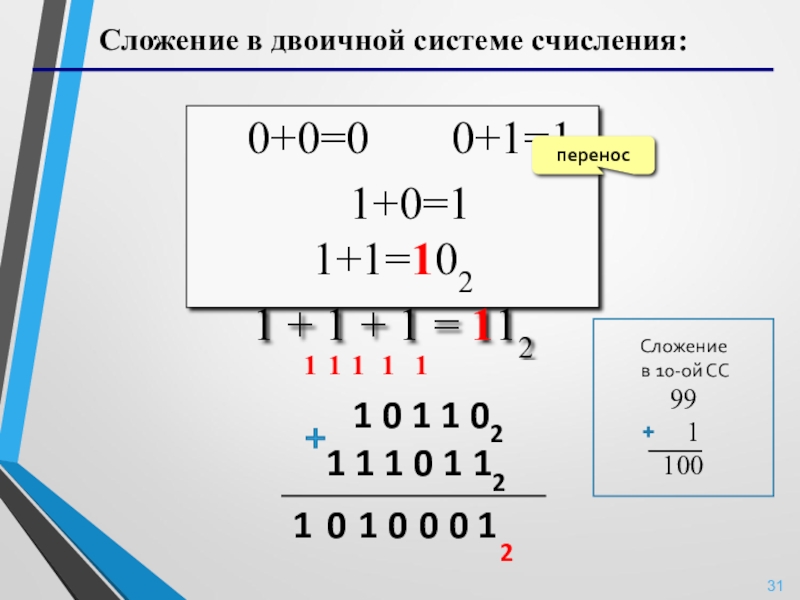
Слайд 31Сложение в двоичной системе счисления:
0+0=0 0+1=1
1 + 1 + 1 = 112
перенос
1 0 1 1 02
1 1 1 0 1 12
1
1
0
0
0
1
1
0
2
1
1
1
1
Сложение
в 10-ой СС
99
1
100
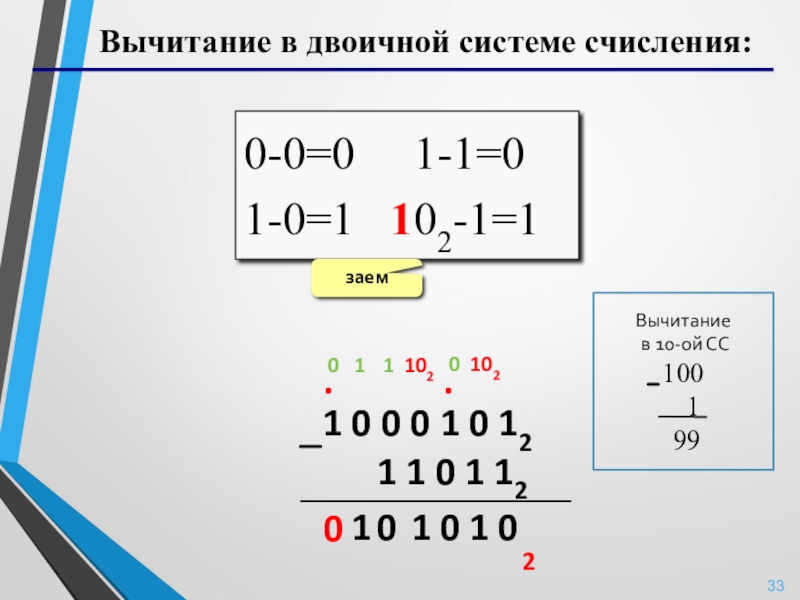
Слайд 33Вычитание в двоичной системе счисления:
0-0=0 1-1=0
1-0=1 102-1=1
заем
1 1 0 1 12
1
∙
∙
0 102
1
0
0 1 1 102
0
1
0
Вычитание
в 10-ой СС
100
1
99
Слайд 37Арифметические операции в 8-ричной СС
сложение
1 5 68
+ 6 6
1
1
6 + 2 = 8 = 1*8 + 0
5 + 6 + 1 = 12 = 1*8 + 4
1 + 6 + 1 = 8 = 1*8 + 0
1
Перенос 1 в след. разряд
Перенос 1 в след. разряд
1
08
0
4
Перенос 1 в след. разряд
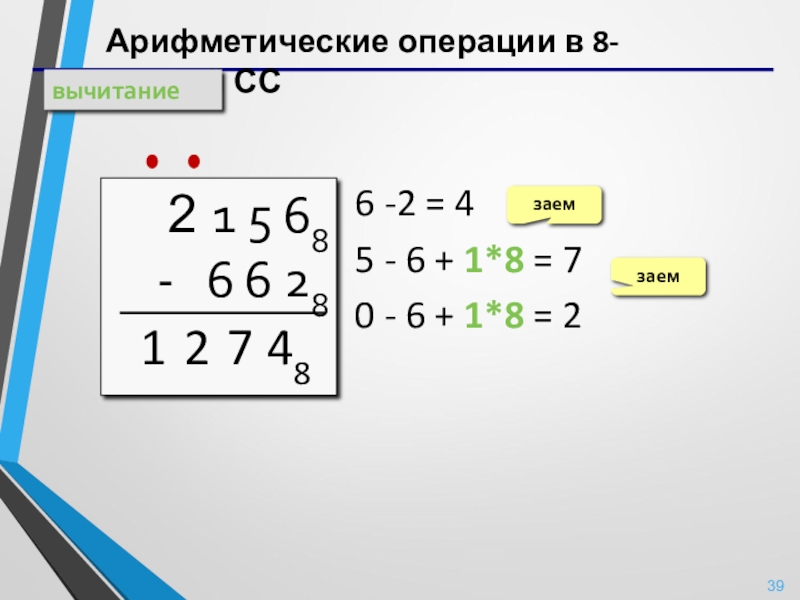
Слайд 39Арифметические операции в 8-ричной СС
вычитание
2 1 5 68
- 6
1
6 -2 = 4
5 - 6 + 1*8 = 7
0 - 6 + 1*8 = 2
заем
48
2
7
заем
Слайд 42Задание №1
1. Переведите числа данные в десятичной СС в двоичную ,
а) 143,25
б) 312,5
2. Переведите данное число в десятичную СС:
а) 10110101,1 б)100100110,10101
Слайд 43ОТВЕТ на задание №1
1. 143,2510 10001111,012
312,510 100111000,12 138,816
2. 10110101,12 181,510
100100110,10112 294,06562510
Слайд 44Задание №2
Переведите в восьмеричную и шестнадцатеричную СС:
110010,1012 1011010011,012
1101111011,012
Слайд 45ОТВЕТ на задание № 2
110010,1012=62,58=32,А16
1011010011,012=1323,28=2D3,416
1101111011,012=1573,28=37B,416
101000010,01112=502,348=142,716
Слайд 46Задание №3
1. Сложите данные числа:
110011001,00112+ 111011101,01012
2. Выполните вычитание:
1101100110,012 – 110000010,10112
3.Выполните умножение:
10011112
Слайд 47Ответ на задание №3
1. 110 011 001,00102 2. 1 101
1 101 110 110,01112 0 111 100 011,10012
3. 1 001 1112
х 1 000 1002
1 010 011 111 1002
Слайд 48Задание №4
1. Переведите число данное в десятичной CC в двоичную ,
а) 67010 б)16210
2. Переведите данное число в десятичную CC:
а) 11111001112 б)10010112
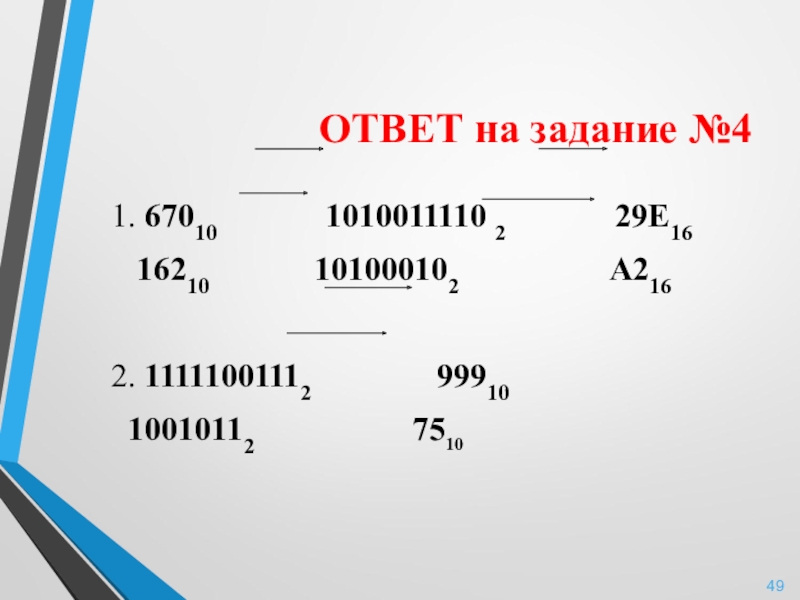
Слайд 49ОТВЕТ на задание №4
1. 67010
16210 101000102 А216
2. 11111001112 99910
10010112 7510
Слайд 50Восстановить неизвестные цифры, обозначенные *, определив вначале в какой системе счисления
А) 5 * 5 5 Б) 1 5 2 6
* 2 2 7 * 4 2
* 1 5 * 4 6 5 4
Решение
А)
5
*
5
5
*
2
2
7
*
1
5
*
4
1) 5+7=12=1 ◾ 8+4 р=8
2) 5+2+1=8=1 ◾ 8+0 *=0
3) *+2+1=5 *=2
4) 5+*=1 5+*=1 ◾ 8+1 *=4
5) *=1
Б)
1
5
2
6
*
4
2
6
5
4
1) 6-2=4
2) 2+р-4=5 р=7
3) 4+7-*=6 *=5
0
2
4
1
5