- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Системы счисления
Содержание
- 1. Презентация по информатике Системы счисления
- 2. Содержание Историческая справкаТеоретический материал2.1. Понятие «система счисления»
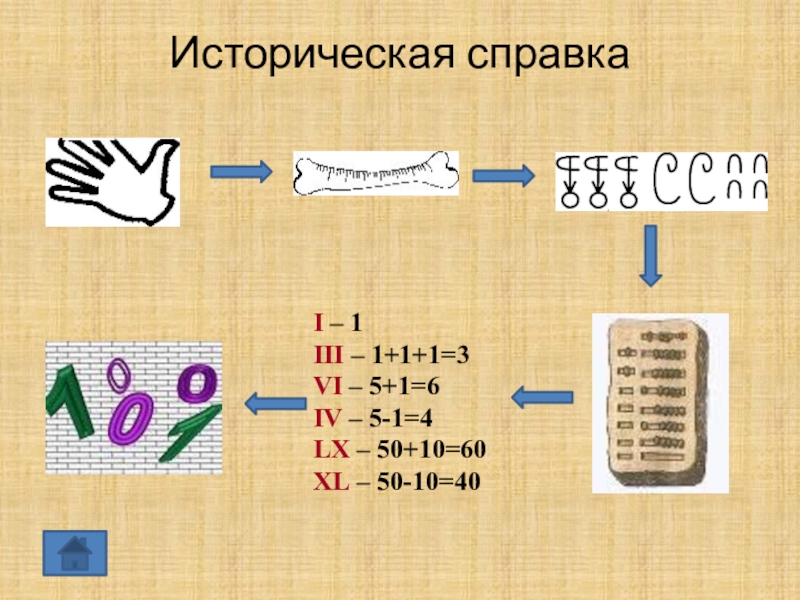
- 3. Историческая справкаI – 1III – 1+1+1=3VI – 5+1=6IV – 5-1=4LX – 50+10=60XL – 50-10=40
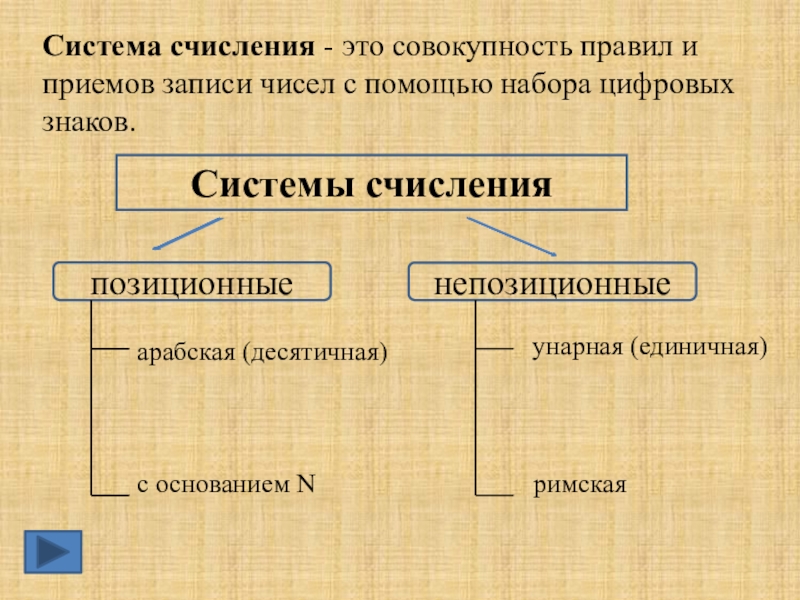
- 4. Системы счисленияпозиционныенепозиционныеСистема счисления - это совокупность правил
- 5. Основные понятия позиционных систем счисленияАлфавитОснование ССМощностьРазрядсовокупность всех
- 6. Арабская система счисленияАрабская система – позиционная десятичная
- 7. Системы счисления с основанием N Если взять правило,
- 8. Унарная система счисленияПервоначально количество предметов отображали равным
- 9. Римская система счисления В римской системе счисления для
- 10. Перевод чисел в десятичную систему счисленияПри переводе
- 11. Последовательно выполнять деление исходного числа и получаемых
- 12. Чтобы перевести число из двоичной системы в
- 13. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное
- 14. Перевод чисел из 16-ой в 8-ю и
- 15. Самостоятельная работа1. Представить римские числа в десятичной
Слайд 2Содержание
Историческая справка
Теоретический материал
2.1. Понятие «система счисления» и Виды систем счисления
позиционные
непозиционные
2.2.
3. Самостоятельная работа
Слайд 4Системы счисления
позиционные
непозиционные
Система счисления - это совокупность правил и приемов записи чисел
арабская (десятичная)
с основанием N
унарная (единичная)
римская
Слайд 5Основные понятия позиционных систем счисления
Алфавит
Основание СС
Мощность
Разряд
совокупность всех цифр
количество цифр, необходимых для
количество цифр, составляющих алфавит
номер позиции в числе
Слайд 6Арабская система счисления
Арабская система – позиционная десятичная система.
Эта система счисления применяется
Основание в десятичной системе равно 10.
Алфавит состоит из 10 цифр:
0 1 2 3 4 5 6 7 8 9
В позиционных системах значение каждой цифры числа определяется ее позицией в записи числа.
Любое число представляется в виде:
765=700+60+5=7*100+6*10+5*1=7*102 +6*101 +5*100
или
76,54=7*10+6*1+5*0,1+4*0,01=7*102+6*101+5*10-1+4*10-2
Слайд 7Системы счисления с основанием N
Если взять правило, по которым строятся числа
В вычислительных машинах используется двоичная система счисления и родственные двоичной - восьмеричная и шестнадцатеричная системы счисления.
Слайд 8Унарная система счисления
Первоначально количество предметов отображали равным количеством каких-либо значков (бирок):
Унарная система сегодня:
счетные палочки для обучения счету;
полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища.
Слайд 9Римская система счисления
В римской системе счисления для записи числа используются латинские
Величина числа получается путем сложения цифр, которыми оно записано. Если слева в записи римского числа стоит меньшая цифра, а справа – большая, то их значения вычитаются, в остальных случаях значения складываются.
I – 1
III – 1+1+1=3
VI – 5+1=6
IV – 5-1=4
LX – 50+10=60
XL – 50-10=40
Слайд 10Перевод чисел в десятичную систему счисления
При переводе числа из двоичной (восьмеричной,
101001102=1*27+0*26+1*25+0*24+0*23+1*22+1
*21+0*20=128+32+4+2=16610
7038=7*82+0*81+3*80=448+3=44710
23FA116=2*164+3*163+15*162+10*161+1*160=1
31072+12288+3840+160+1=147361
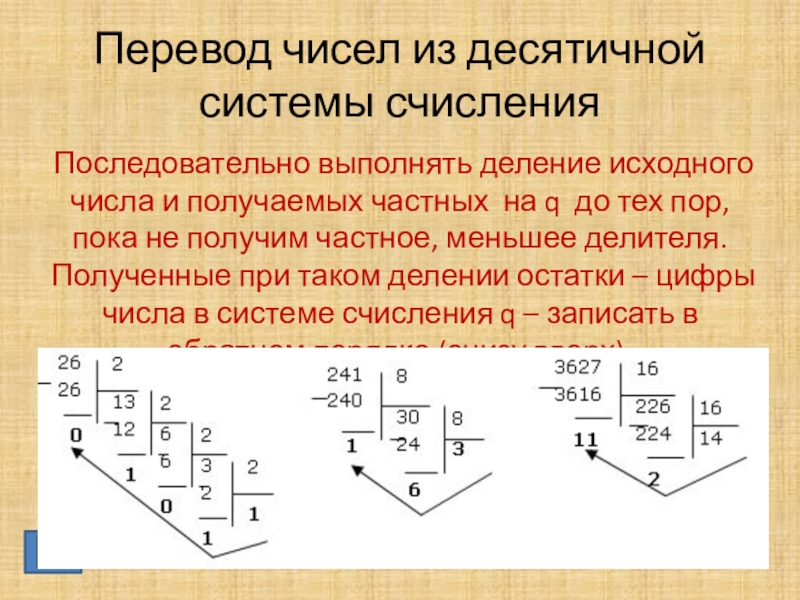
Слайд 11Последовательно выполнять деление исходного числа и получаемых частных на q до
Перевод чисел из десятичной системы счисления
Слайд 12Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно
010 010 110 1112=22678
0100 1011 01112=4В716
Перевод чисел из двоичной системы счисления
Слайд 13Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить
7268= 111 010 1102
74С16 = 0111 0100 11002
(при записи числа первый 0 не пишется)
Перевод чисел в двоичную систему счисления
Слайд 14Перевод чисел из 16-ой в 8-ю и обратно
FAE16=1111101011102
111 110 101 1102=76568
6358 =1100111012
1 1001
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Слайд 15Самостоятельная работа
1. Представить римские числа в десятичной системе счисления: CDIX, CVXLIX,
2. Перевести число 93710 в 2-ную, 8-ную и 16-ную системы счисления.
3. Перевести из 8 -ой системы счисления в 2-ную 764 и 312
4. Перевести следующие числа в десятичную систему счисления:
а) 1101012; б) 10110001; в) 5638; г) 6358; д) AC416; е) 9D5C16.