- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Системы счисления
Содержание
- 1. Презентация по информатике Системы счисления
- 2. Система счисления – это способ представления чисел и соответствующие ему правила действия над числами.
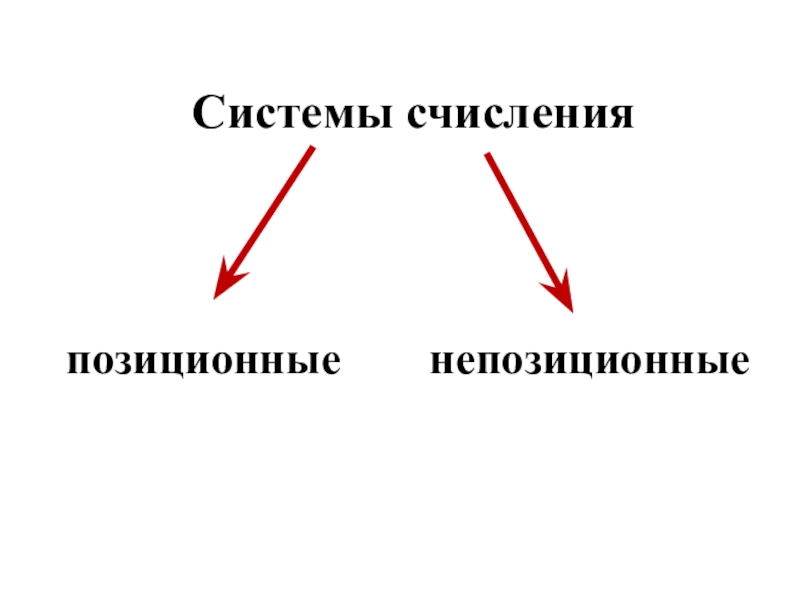
- 3. Системы счисленияпозиционныенепозиционные
- 4. В непозиционных системах счисления от положения цифры
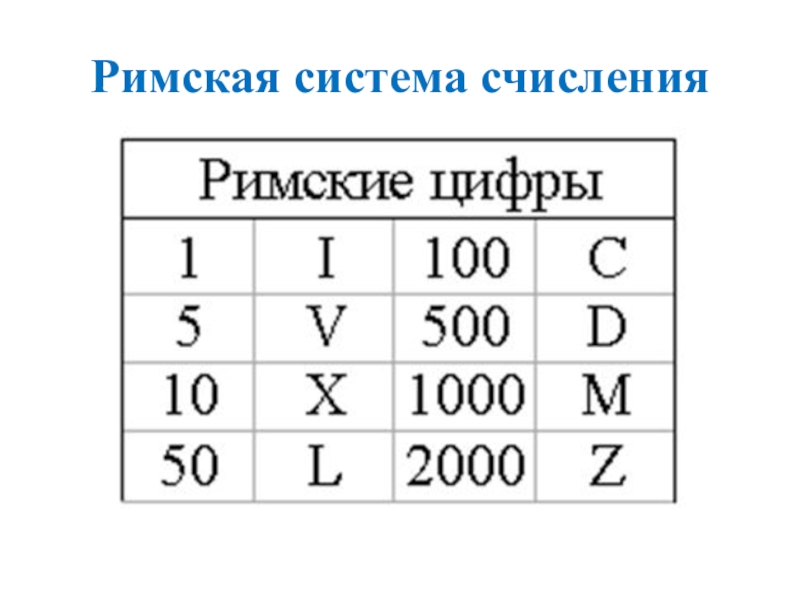
- 5. Римская система счисления
- 6. Правило первоеВ римских числах цифры записываются слева
- 7. Правило второеЕсли римских числах слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
- 8. Перевести числа из римской системы счисления в
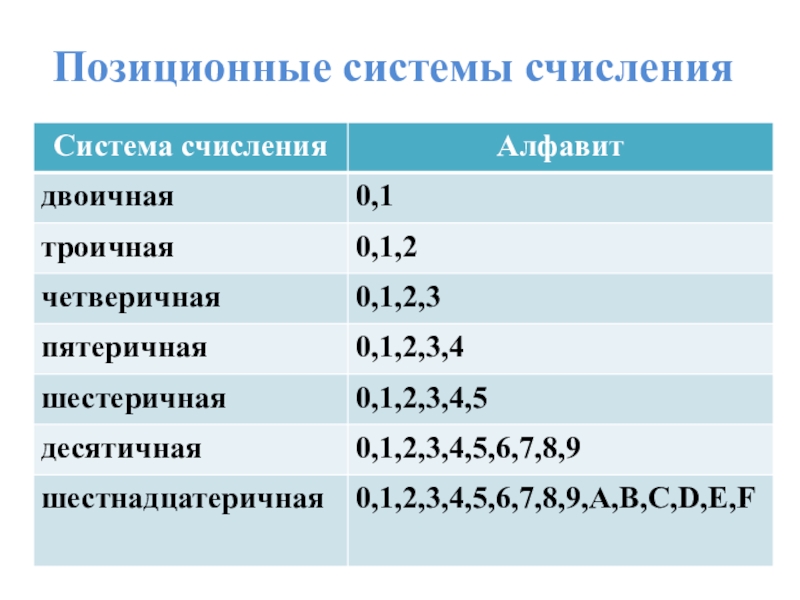
- 9. Позиционные системы счисления
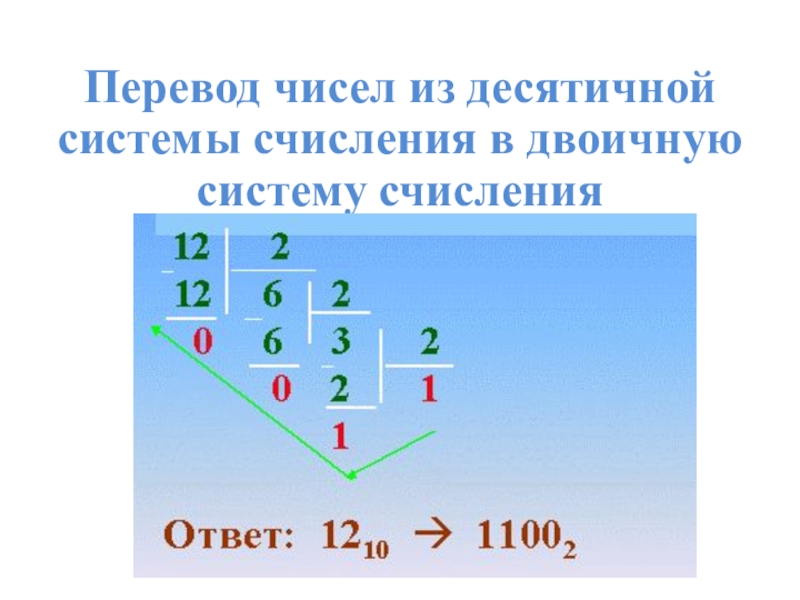
- 10. Перевод чисел из десятичной системы счисления в двоичную систему счисления
- 11. Перевод чисел из двоичной системы счисления в десятичную систему счисления1012=1· 22 +0· 21 + 1· 20=510
- 12. ЗАДАНИЯ№1 Перевести:225338 = 10010101011011210010101111002 = 12BC16101010100111002 = 2523481C6316 = 11100011000112№2 Решение
- 13. Перевод чисел из двоичной системы счисления в
- 14. Перевод чисел из двоичной системы счисления в
- 15. Для перевода чисел из восьмеричной и шестнадцатеричной
- 16. Сложение чисел в двоичной системе счисленияПравила1+1=101+0=00+1=10+0=0
- 17. Сложение чисел в двоичной системе счисления101010+1111111=1100110+101011=1110111+1100101=1011111+1111=1010111+1011=
- 18. Десятичные дроби в системах счисления
- 19. Пpи переводе десятичной дpоби в систему счисления с
- 20. ПримерыОтвет: 0,3510 = 0,010112 = 0,2638 = 0,5916
- 21. Перевод дроби в десятичную систему счисления1000001001,1012 = (1·
- 22. Задачи ЕГЭРешите уравнение Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
- 23. Дано А = Е716, B = 2438.
- 24. Дано: а = 7010, b = 1008
- 25. Запись числа 6710 в системе счисления с
- 26. Запись десятичного числа в системах счисления с
- 27. Укажите через запятую в порядке возрастания все
- 28. Даны 4 числа, они записаны с использованием
Система счисления – это способ представления чисел и соответствующие ему правила действия над числами.
Слайд 2Система счисления – это способ представления чисел и соответствующие ему правила
действия над числами.
Слайд 4В непозиционных системах счисления от положения цифры в записи числа не
зависит величина, которую она обозначает.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции.
Слайд 6Правило первое
В римских числах цифры записываются слева направо в порядке убывания.
В таком случае их значения складываются.
Слайд 7Правило второе
Если римских числах слева записана меньшая цифра, а справа –
большая, то их значения вычитаются.
Слайд 8Перевести числа из римской системы счисления в десятичную систему счисления
MCM; MIV;
MXL; MMMIV; MXCIX; CCCXLVII; DCCXCVIII; CCXVI
Слайд 11Перевод чисел из двоичной системы счисления в десятичную систему счисления
1012=1· 22 +0·
21 + 1· 20=510
Слайд 12ЗАДАНИЯ
№1 Перевести:
225338 = 100101010110112
10010101111002 = 12BC16
101010100111002 = 252348
1C6316 = 11100011000112
№2 Решение неравенств.
Поставьте вместо знака
? знак <, > или =.
28510 ? 11D16 (Ответ: 28510 = 28510 )
1111112 ? 11118 (Ответ: 6310 < 58510 )
6С16 ? 1010012 (Ответ: 10810 > 4110 )
5516 ? 1258 (Ответ: 8510 = 8510 )
№3 Числовые последовательности.
Расположите числа, записанные в различных системах счисления, в порядке возрастания:
3510, 368, 3А16, 1001012 (Ответ: 368, 3510, 1001012, 3А16 )
1110012, 648, 9Е16, 2510 (Ответ: 2510, 648, 1110012, 9Е16 )
28510 ? 11D16 (Ответ: 28510 = 28510 )
1111112 ? 11118 (Ответ: 6310 < 58510 )
6С16 ? 1010012 (Ответ: 10810 > 4110 )
5516 ? 1258 (Ответ: 8510 = 8510 )
№3 Числовые последовательности.
Расположите числа, записанные в различных системах счисления, в порядке возрастания:
3510, 368, 3А16, 1001012 (Ответ: 368, 3510, 1001012, 3А16 )
1110012, 648, 9Е16, 2510 (Ответ: 2510, 648, 1110012, 9Е16 )
Слайд 13Перевод чисел из двоичной системы счисления в восьмеричную.
Для перевода целого двоичного
числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 1010012 в восьмеричное:
101 0012 => 1 × 22 + 0 × 21 + 1 × 20 =5 0 × 22 + 0 × 21 + 1 × 20 => 1
Ответ: 1010012 = 518
Переведем таким способом двоичное число 1010012 в восьмеричное:
101 0012 => 1 × 22 + 0 × 21 + 1 × 20 =5 0 × 22 + 0 × 21 + 1 × 20 => 1
Ответ: 1010012 = 518
Слайд 14Перевод чисел из двоичной системы счисления в шестнадцатеричную.
Для перевода целого
двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями.
Слайд 15Для
перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную
необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа - в группу из четырех цифр (тетраду).
Слайд 17Сложение чисел в двоичной системе счисления
101010+1111111=
1100110+101011=
1110111+1100101=
1011111+1111=
1010111+1011=
Слайд 19 Пpи переводе десятичной дpоби в систему счисления с основанием q необходимо сначала саму
дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.
Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности.
Слайд 21Перевод дроби в десятичную систему счисления
1000001001,1012 = (1· 29 + 0· 28 + 0·
27 + 0· 26 + 0· 25+ 0· 24 + 1· 23 + 0· 22 + 0· 21 + 1· 20 +1· 2-1 + 0· 2-2 +1· 2-3)10 = (512 + 8 + 1 + 1/2 + 1/8)10 = (521+5/8)10 = (521,625)10
Слайд 22Задачи ЕГЭ
Решите уравнение
Ответ запишите в шестеричной системе счисления. Основание системы
счисления указывать не нужно.
Слайд 24Дано: а = 7010, b = 1008 Какое из чисел с,
записанных в двоичной системе, отвечает условию b < с < a?
1) 10000002
2) 10001102
3) 10001012
4) 10001112
1) 10000002
2) 10001102
3) 10001012
4) 10001112
Слайд 25Запись числа 6710 в системе счисления с основанием N оканчивается на
1 и содержит 4 цифры. Укажите основание этой системы счисления N.
Слайд 26Запись десятичного числа в системах счисления с основаниями 3 и 5
в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Слайд 27Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие
25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Слайд 28Даны 4 числа, они записаны с использованием различных систем счисления. Укажите
среди этих чисел то, в двоичной записи которого содержится ровно 6 единиц. Если таких чисел несколько, укажите наибольшее из них.