- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Система счисления
Содержание
- 1. Презентация по информатике Система счисления
- 2. *Система счисленияСовокупность символов, используемых для изображения чисел.
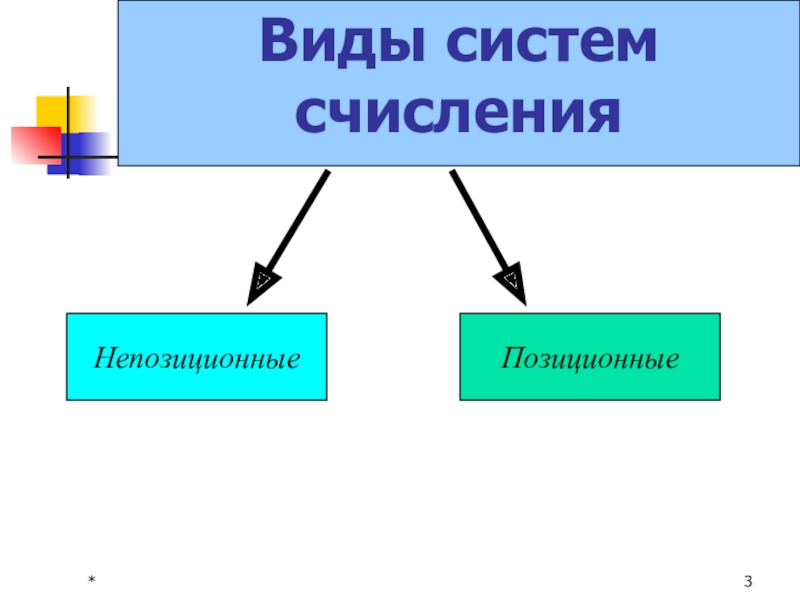
- 3. *Непозиционные Позиционные Виды систем счисления
- 4. *Римская непозиционная система счисленияВ качестве цифр в
- 5. *Позиционные системы счисленияВ позиционных системах счисления количественное
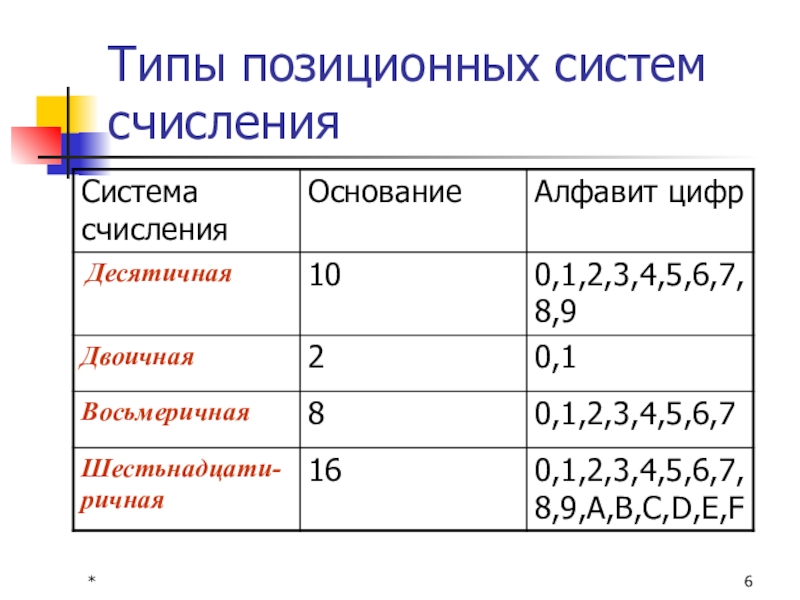
- 6. *Типы позиционных систем счисления
- 7. *Разрядная сетка десятичной системы счисления
- 8. *Позиционные системы с произвольным основаниемгде q-основание системы
- 9. *Разрядная сетка двоичной системы счисления1⋅2-3+0⋅2-2+1⋅2-1+1 ⋅20+1 ⋅21+0 ⋅22+1 ⋅23=0.008+0.2+1+2+8=11,20810
- 10. *Развернутая форма числа: - в двоичной системе счисленияА2=an*2n+an-1*2n-1+…+a0*20+a-1*2-1+ …+a-m*2-m- в десятичной системе счисленияА=an*10n+an-1*10n-1+…+a0*100+a-1*10-1+ …+a-m*10-m
- 11. *Правило перевода чисел в двоичную систему счисления
- 12. *12410
- 13. *15010
- 14. *1110002 х10 1101102
- 15. *Сложение чисел в двоичной системе счисленияДля сложения
- 16. *Вычитание чисел в двоичной системе счисленияДля вычитания
- 17. *Умножение чисел в двоичной системе счисленияТаблица умножения
- 18. *Деление чисел в двоичной системе счисленияТак же,
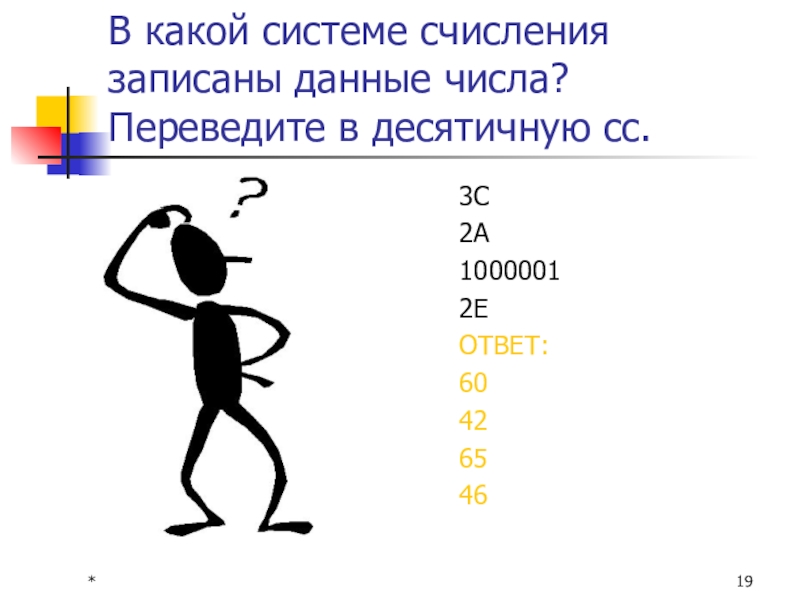
- 19. *В какой системе счисления записаны данные числа? Переведите в десятичную сс.3C2А10000012ЕОТВЕТ:60426546
*Система счисленияСовокупность символов, используемых для изображения чисел.
Слайд 4*
Римская непозиционная система счисления
В качестве цифр в римской системе используются: I(1),
II (2), III(3), V(5), X(10), L(50), C(100), D(500), M(1000).
Значение цифры не зависит от ее положения в числе.
Например: МDLVIII - 1558
Значение цифры не зависит от ее положения в числе.
Например: МDLVIII - 1558
Слайд 5*
Позиционные системы счисления
В позиционных системах счисления количественное значение цифры зависит от
ее позиции (местоположения)в числе.
Позиция цифры в числе называется разрядом. Вес разряда определяется как основание счисления в степени, равной номеру разряда.
Каждая позиционная система счисления имеет определенный алфавит цифр и основание.
Основание системы равно количеству цифр (знаков в алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов.
Позиция цифры в числе называется разрядом. Вес разряда определяется как основание счисления в степени, равной номеру разряда.
Каждая позиционная система счисления имеет определенный алфавит цифр и основание.
Основание системы равно количеству цифр (знаков в алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов.
Слайд 8*
Позиционные системы с произвольным основанием
где q-основание системы счисления
Любое число, независимо от
основания системы счисления, образуется как сумма произведений цифры числа на вес соответствующего разряда
Аq=an*qn+an-1*qn-1+…+a0*q0+a-1*q-1+ …+a-m*q-m
583,35=5⋅10-2 + 3⋅10-1 + 3⋅100 + 8⋅101 + 5⋅102=0,05+0,3+3+80+500
Слайд 9*
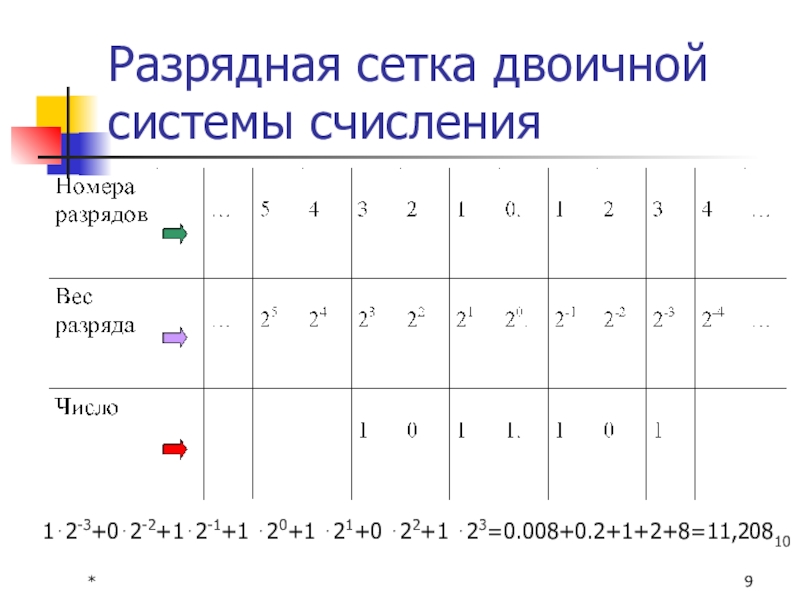
Разрядная сетка двоичной системы счисления
1⋅2-3+0⋅2-2+1⋅2-1+1 ⋅20+1 ⋅21+0 ⋅22+1 ⋅23=0.008+0.2+1+2+8=11,20810
Слайд 10*
Развернутая форма числа:
- в двоичной системе счисления
А2=an*2n+an-1*2n-1+…+a0*20+a-1*2-1+ …+a-m*2-m
- в десятичной системе
счисления
А=an*10n+an-1*10n-1+…+a0*100+a-1*10-1+ …+a-m*10-m
А=an*10n+an-1*10n-1+…+a0*100+a-1*10-1+ …+a-m*10-m
Слайд 11*
Правило перевода чисел в двоичную систему счисления
Целые числа кодируются двоичным
кодом делением числа на основание степени (2) до тех пор, пока частное от деления не будет равно единице.
Например: для перевода числа 124 в десятичной системе счисления в двоичную следует провести следующие операции
Например: для перевода числа 124 в десятичной системе счисления в двоичную следует провести следующие операции
Слайд 12*
12410 х2
124I2
124I62I2
0
62I31I2
030I15I2
1 14I7I2
1 6I3I2 Ответ:
1I2I1 X= 11111002
1
Проверка:
11111002=1*26+1*25+1*24+1*23+1*22+0*21+ 0*20=64+32+16+8+4=12410
030I15I2
1 14I7I2
1 6I3I2 Ответ:
1I2I1 X= 11111002
1
Проверка:
11111002=1*26+1*25+1*24+1*23+1*22+0*21+ 0*20=64+32+16+8+4=12410
Слайд 13*
15010 х2 19010
х2
36010 х2 13410 х2
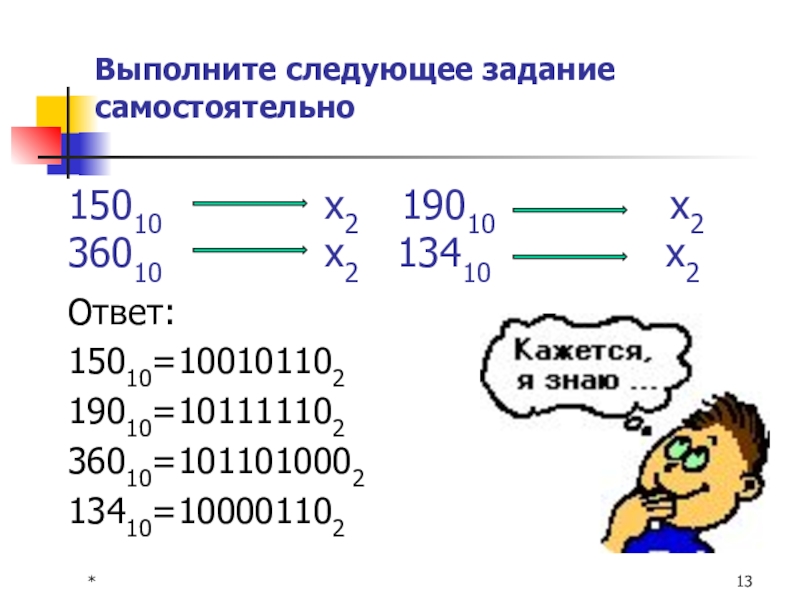
Ответ:
15010=100101102
19010=101111102
36010=1011010002
13410=100001102
Выполните следующее задание самостоятельно
Слайд 14*
1110002 х10
1101102 х10
Ответ:
1110002=5610
1101102=5410
Перевод
чисел из двоичной системы счисления в десятичную
Слайд 15*
Сложение чисел в двоичной системе счисления
Для сложения используется следующая таблица:
0+0=0
0+1=1
1 +
0 = 1
1 + 1 = 10 (при сложении двух единиц получается единица в более старшем разряде)
1 + 1 = 10 (при сложении двух единиц получается единица в более старшем разряде)
101
+
100
------
1001
1100
+
11
110
--------
10101
100
+
11
10
-------
1001
Слайд 16*
Вычитание чисел в двоичной системе счисления
Для вычитания используется следующая таблица:
0 -
0 = 0
1 - 1 =
1 - 0 = 1
10 - 1 = 1 (при вычитания 1 из 0 необходимо занять 1 из более старшего разряда)
1 - 1 =
1 - 0 = 1
10 - 1 = 1 (при вычитания 1 из 0 необходимо занять 1 из более старшего разряда)
111
-
110
-------
1
110
-
10
------
100
1001
-
11
--------
110
Слайд 17*
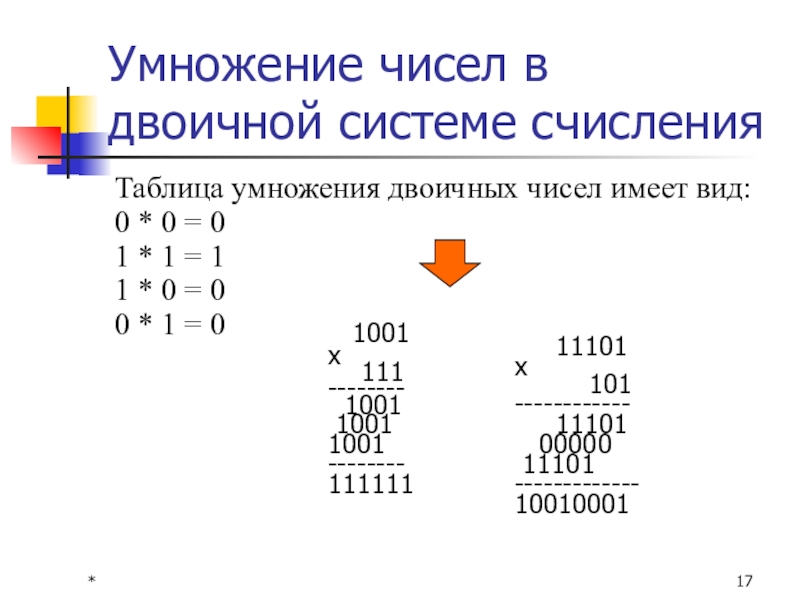
Умножение чисел в двоичной системе счисления
Таблица умножения двоичных чисел имеет вид:
0
* 0 = 0
1 * 1 = 1
1 * 0 = 0
0 * 1 = 0
1 * 1 = 1
1 * 0 = 0
0 * 1 = 0
1001
x
111
--------
1001
1001
1001
--------
111111
11101
x
101
------------
11101
00000
11101
-------------
10010001
Слайд 18*
Деление чисел в двоичной системе счисления
Так же, как умножение может быть
заменено
многократным сложением и сдвигом влево, деление может
быть заменено многократным вычитанием и сдвигом в право.
многократным сложением и сдвигом влево, деление может
быть заменено многократным вычитанием и сдвигом в право.
110 : 10 =11
-
10
--------
10
-
10
--------
0
1100 : 11 =100
-
11
-------
0
Слайд 19*
В какой системе счисления записаны данные числа?
Переведите в десятичную сс.
3C
2А
1000001
2Е
ОТВЕТ:
60
42
65
46
