- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Решение оптимизационных задач в среде электронных таблиц MS Exsel (11 класс)
Содержание
- 1. Презентация по информатике Решение оптимизационных задач в среде электронных таблиц MS Exsel (11 класс)
- 2. Решение оптимизационных задач в среде электронных таблиц
- 3. Решение оптимизационных задач в среде электронных таблиц
- 4. Задача1. Пусть в колхозе требуется
- 5. Решение оптимизационных задач в среде электронных таблиц
- 6. Решение оптимизационных задач в среде электронных таблиц
- 7. Решение оптимизационных задач в среде электронных таблиц
- 8. Решение оптимизационных задач в среде электронных таблиц
- 9. Решение оптимизационных задач в среде электронных таблиц
- 10. Решение оптимизационных задач в среде электронных таблиц
- 11. Решение оптимизационных задач в среде электронных таблиц
- 12. Решение оптимизационных задач в среде электронных таблиц
- 13. Решение оптимизационных задач в среде электронных таблиц
- 14. Решение оптимизационных задач в среде электронных таблиц ExcelОграничения:Целевая функция:
- 15. Решение оптимизационных задач в среде электронных таблиц
- 16. Решение оптимизационных задач в среде электронных таблиц ExcelОграничения: Целевая функция:
- 17. Решение оптимизационных задач в среде электронных таблиц
- 18. Решение оптимизационных задач в среде электронных таблиц ExcelОграничения: Целевая функция:
Слайд 2Решение оптимизационных задач в среде электронных таблиц Excel
С помощью надстроек
Поиск решения является надстройкой, которая позволяет решать задачи оптимизационного моделирования.
Слайд 3Решение оптимизационных задач в среде электронных таблиц Excel
Для установки надстройки
Поиск
Знак оффиса в левом верхнем углу Excel
Копка «Параметры Excel»
Вкладка «Надстройки» → Перейти
установить флажок около пункта Поиск решения;
щелкнуть на кнопке ОК.
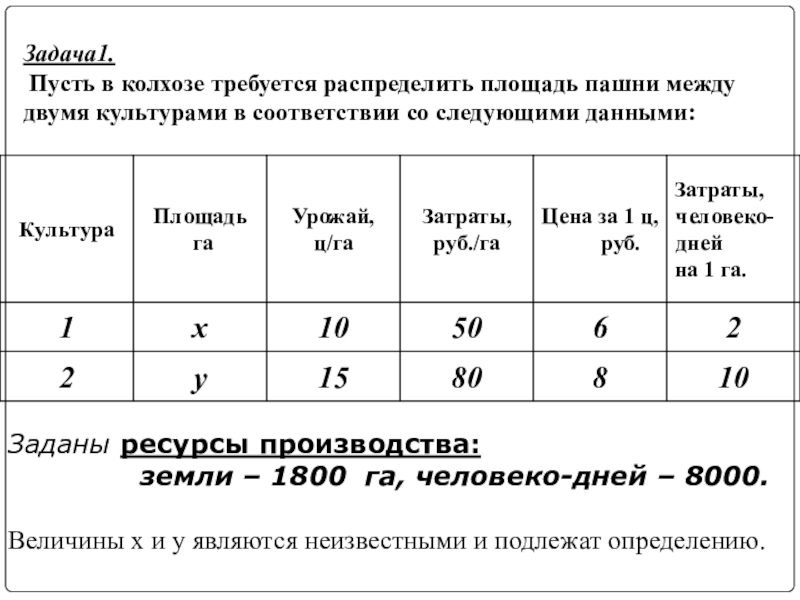
Слайд 4Задача1. Пусть в колхозе требуется распределить площадь пашни между двумя
Заданы ресурсы производства:
земли – 1800 га, человеко-дней – 8000.
Величины x и y являются неизвестными и подлежат определению.
Слайд 5Решение оптимизационных задач в среде электронных таблиц Excel
Построение математической модели задачи
задание целевой функции (ее надо максимизировать или минимизировать);
задание системы ограничений в форме линейных уравнений и неравенств;
Требование неотрицательности переменных.
Слайд 6Решение оптимизационных задач в среде электронных таблиц Excel
Решим задачу по оптимизации
Для прибыли (согласно данным таблицы) имеем формулу:
Слайд 7Решение оптимизационных задач в среде электронных таблиц Excel
Ограничения имеют следующий вид:
ограничение
ограничение по человеко-дням:
или
Кроме того, ясно, что
Слайд 8Решение оптимизационных задач в среде электронных таблиц Excel
Учтя все условия задачи,
неотрицательных целочисленных решений системы линейных неравенств
Среди них найти такие, которые соответствуют максимуму линейной функции
Слайд 9Решение оптимизационных задач в среде электронных таблиц Excel
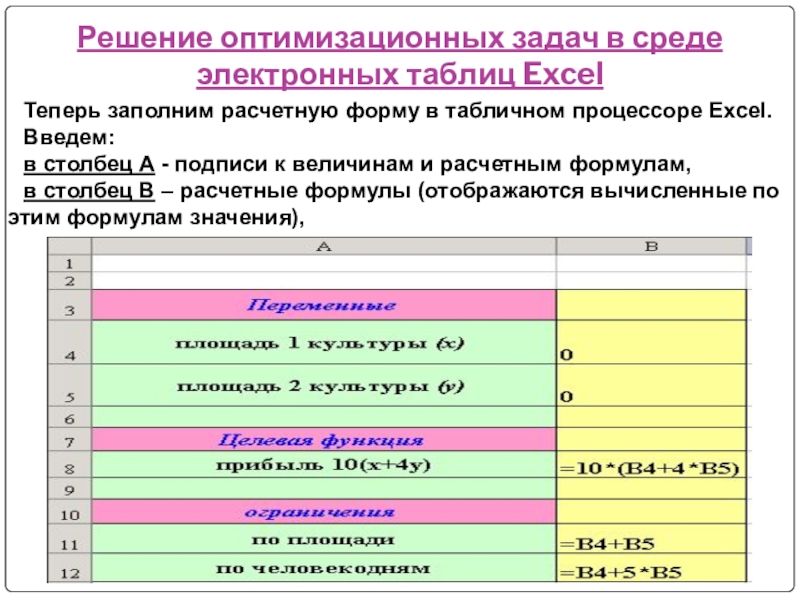
Теперь заполним расчетную форму
Введем:
в столбец А - подписи к величинам и расчетным формулам,
в столбец В – расчетные формулы (отображаются вычисленные по этим формулам значения),
Слайд 10Решение оптимизационных задач в среде электронных таблиц Excel
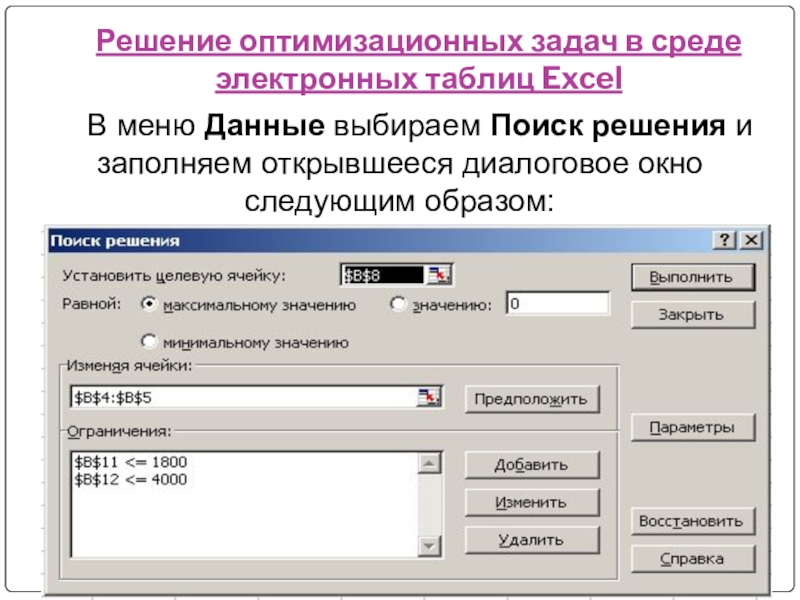
В меню Данные выбираем
Слайд 11Решение оптимизационных задач в среде электронных таблиц Excel
Далее щелкаем в этом
и в открывшемся диалоговом окне Параметры поиска решения устанавливаем флажки Линейная модель и Неотрицательные значения. Щелкаем по кнопке ОК.
В окне Поиск решения щелкаем на кнопке Выполнить.
Слайд 12Решение оптимизационных задач в среде электронных таблиц Excel
Задача 2.
Предполагается, что рацион
Суточная потребность кормов на 1 корову равна 20 кормовых единиц.
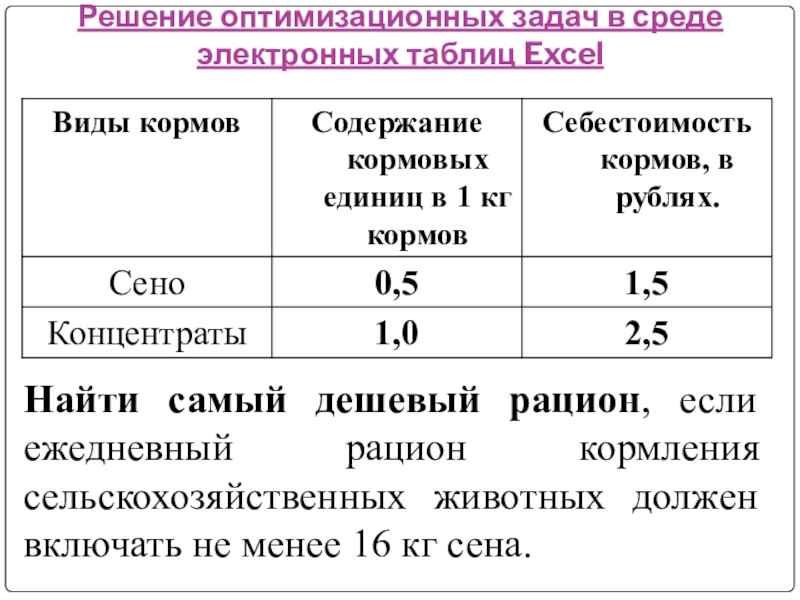
В таблице приведены числовые данные о себестоимости кормов в данном хозяйстве.
Слайд 13Решение оптимизационных задач в среде электронных таблиц Excel
Найти самый дешевый рацион,
Слайд 15Решение оптимизационных задач в среде электронных таблиц Excel
Задача3.
Мебельная фабрика
Известно, что цена одного кресла первого типа равна 1500 рублей, второго типа – 2000 рублей. Сколько кресел каждого типа надо выпускать, чтобы стоимость выпускаемой продукции была максимальной, если фабрика имеет в наличии 4400 м досок, 1500 м2 обивочной ткани и может затратить 3200 человеко-часов рабочего времени на изготовление этой продукции?
Слайд 17Решение оптимизационных задач в среде электронных таблиц Excel
Задача 4
При этом должно быть учтено следующее:
1ц кукурузного силоса содержит 0,2 кормовой единицы, 1ц свеклы – 0,26 кормовой единицы;
на возделывание 1га кукурузного поля необходимо затратить 38 человеко-часов труда механизаторов и 15 человеко-часов ручного труда, а на возделывание 1га поля, занятого свеклой, соответственно 43 и 185 человеко-часов;
ожидаемый урожай кукурузы – 500 ц с 1 га, а свеклы – 200 ц с 1 га;
наконец, всего на возделывание кормовых культур можно затратить 4000 человеко-часов механизаторов и 15000 человеко-часов ручного труда.