Козина С.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Прикладное применение гиперболических параболоидов
Содержание
- 1. Презентация по информатике Прикладное применение гиперболических параболоидов
- 2. Архитектурные возможности гипаров
- 3. Вид поверхности, получивший название гиперболического параболоида, или
- 4. Феликс Кандела «Тот же самый архитектор, который
- 5. Феликс Кандела родился 27 января 1910 года
- 6. Его целью было разработать структурную механику сводчатых
- 7. 1952 год в Мехико построен павильон «Космические
- 8. Церковь в Мехико (1953 г.)
- 9. Часовня Ломас-де-Куэрнавака (1958 г.)
- 10. Казино Де ла Сельва в Мехико (1960 г.)
- 11. Капелла Санта Моника (1968 г.)
- 12. дворец спорта в Мехико (1968 г.)
- 13. Церковь в Сан-Хосе (1994 г.)
- 14. Iglesia de la Virgen de la Medalla Milagrosa(Иглесия-де-ла-Вирхен-де-ла-Medalla Milagrosa)
- 15. В 1998 году в Валенсии был официально открыт Город Искусств
- 16. Производственное здание Bacardi Rum FactoryВ историю архитектуры
- 17. Производственное здание Bacardi Rum FactoryВ связи с
- 18. Феликс Кандела сказал однажды: «Я раскрыл свои
- 19. Цель: с помощью редактора Excel
- 20. В ячейках А1 и В2 находятся параметры
- 21. Вводим значения в таблицу Excel: В ячейках
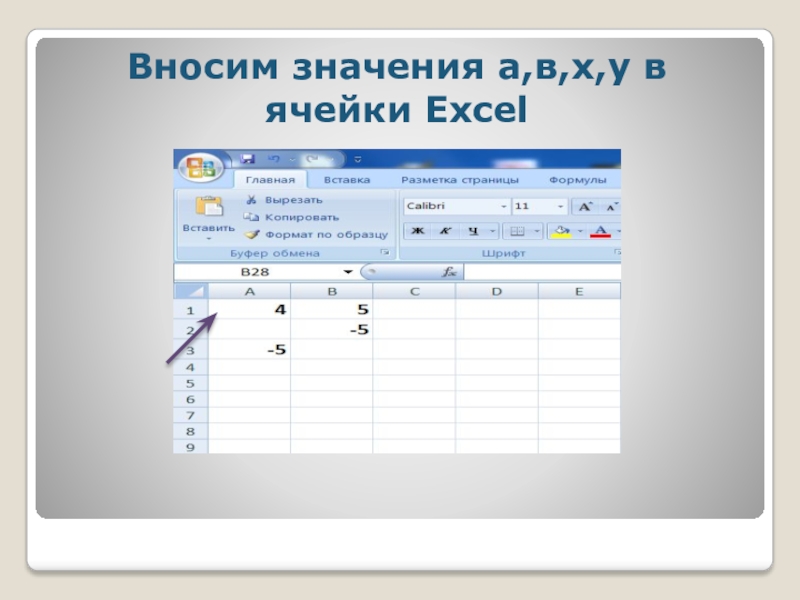
- 22. Вносим значения а,в,х,у в ячейки Excel
- 23. Для получения ряда данных, вычисляемых
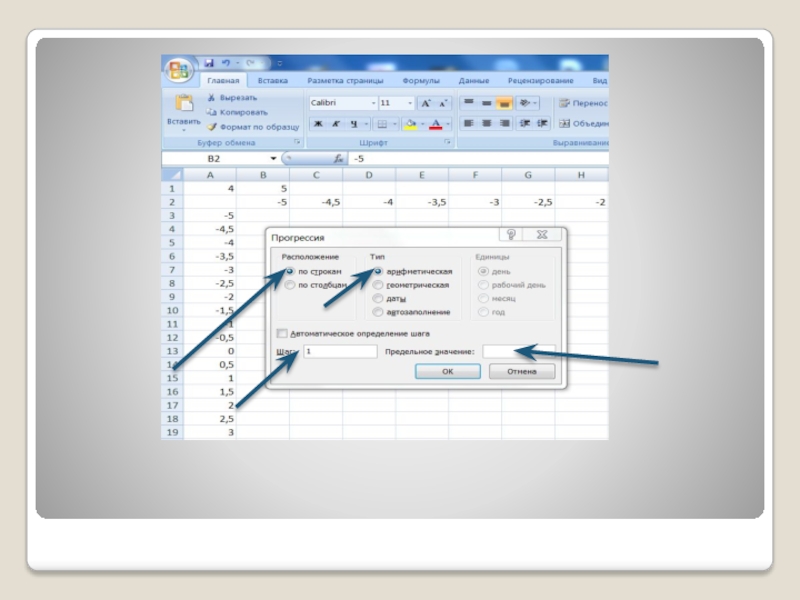
- 24. Выполните команду Редактирование ,
- 25. Слайд 25
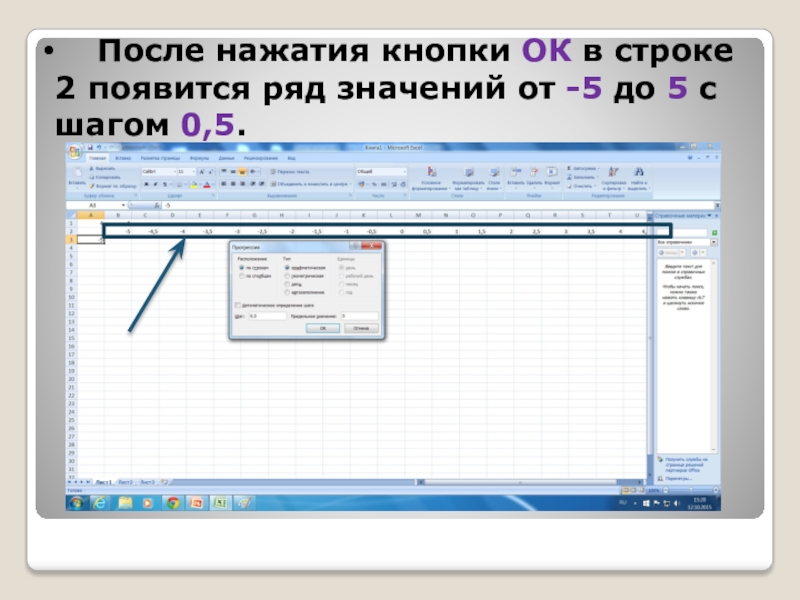
- 26. После нажатия кнопки ОК в
- 27. Мы ввели область изменения переменной х. Аналогичные
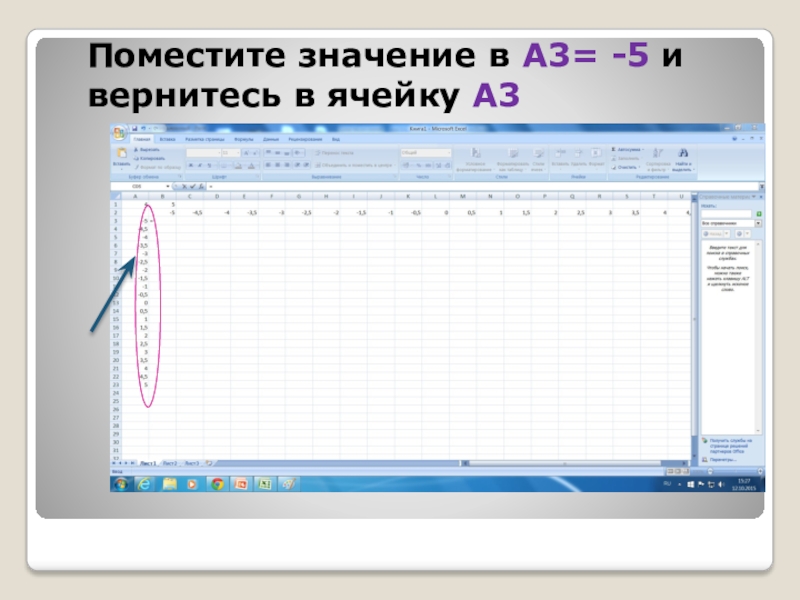
- 28. Поместите значение в А3= -5 и вернитесь в ячейку А3
- 29. Теперь введем формулы для вычисления значений
- 30. Далее распространите эту формулу на всю строку,
- 31. Автозаполнение ячеек
- 32. Постройте трехмерную диаграмму типа "Поверхность" по областям
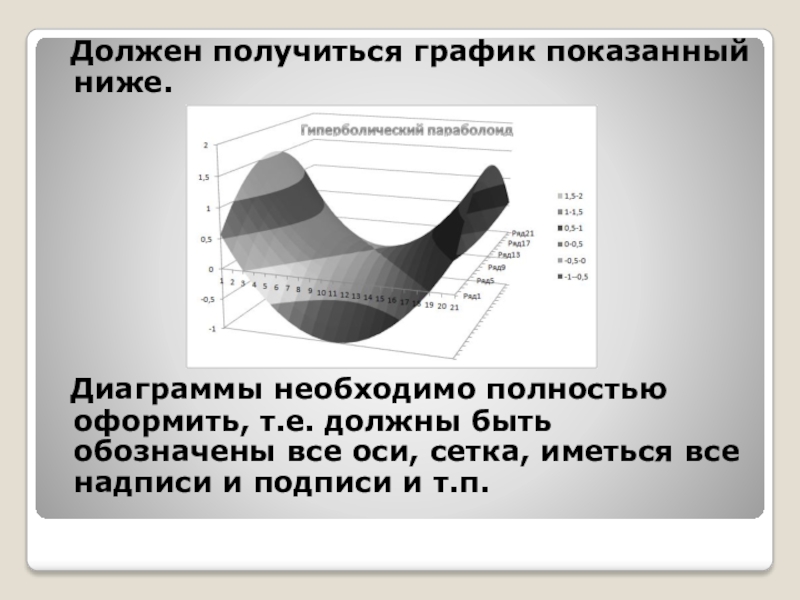
- 33. Должен получиться график показанный ниже. Диаграммы
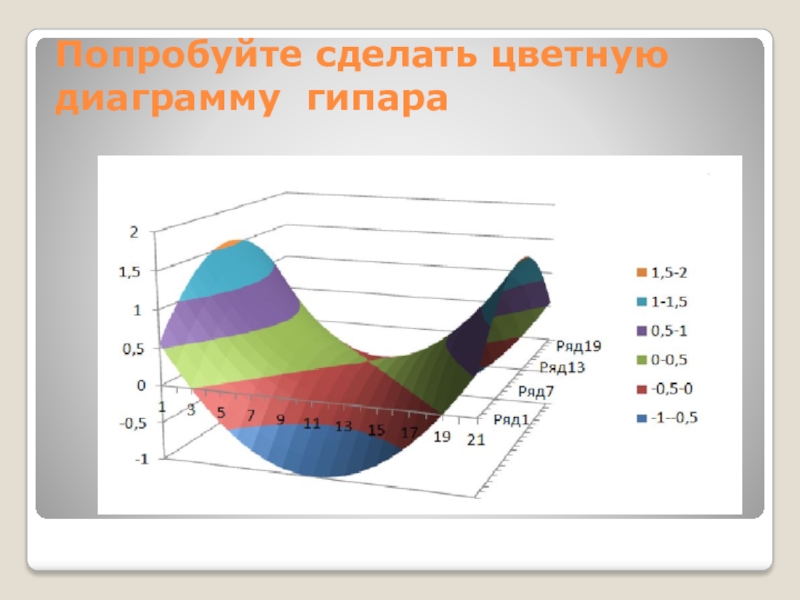
- 34. Попробуйте сделать цветную диаграмму гипара
- 35. Выставочный комплекс Экспо 67 в Монреале, архитектор
- 36. Феликс Кандела
- 37. Феликс Кандела «Я начал изучать архитектуру совершенно
- 38. Благодарим за внимание!
Архитектурные возможности гипаров были открыты испанским архитектором Феликсом Канделой. Различные сооружения: Промышленные здания Церкви Характерны: Экономичность и изящество Архитектура напоминает готическуюПроизводственное здание Bacardi
Слайд 1Прикладное применение динамических
таблиц
при проектировании архитектурных конструкций
в виде гиперболических параболоидов
Разработала:
Слайд 2
Архитектурные возможности гипаров были открыты испанским архитектором
Феликсом Канделой.
Различные сооружения:
Промышленные здания
Церкви
Характерны:
Экономичность и изящество
Архитектура напоминает готическую
Различные сооружения:
Промышленные здания
Церкви
Характерны:
Экономичность и изящество
Архитектура напоминает готическую
Производственное здание Bacardi Rum Factory
Слайд 3
Вид поверхности, получивший название гиперболического параболоида, или коротко гипара, образуется одной
прямой линией, движущейся по двум прямым линиям, которые наклонены под углом одна к другой.
Слайд 4Феликс Кандела
«Тот же самый архитектор, который понятия не имеет, как работает
опорная балка, считает себя достаточно квалифицированным,
чтобы создавать экстраординарные конструкции».
Эстетическое совершенство его построек было обусловлено прежде всего конструкторским, а не дизайнерским подходом.
чтобы создавать экстраординарные конструкции».
Эстетическое совершенство его построек было обусловлено прежде всего конструкторским, а не дизайнерским подходом.
Слайд 5Феликс Кандела родился 27 января 1910 года в Мадриде.
В 1935
году он получил диплом выпускника Высшей Технической Школы Архитектуры.
Слайд 6Его целью было разработать структурную механику сводчатых покрытий.
1939 год. –
служба в республиканских войсках
Лагерь в Перпиньян
Переезд в Мексику
1941 год – мексиканское гражданство
Лагерь в Перпиньян
Переезд в Мексику
1941 год – мексиканское гражданство
Слайд 71952 год в Мехико построен павильон «Космические лучи» (Cosmic Rays pavilion)
для Национального Автономного Университета Мехико - первый пример создания крыши в форме гиперболического параболоида, или гипара.
Слайд 16Производственное здание Bacardi Rum Factory
В историю архитектуры Феликс Кандела вошел в
качестве создателя железобетонных конструкций – оболочек типа гиперболического параболоида, которые характеризовались высокой экономичностью одновременно с большим разнообразием формообразования. Кроме этого, работы Канделы отличались важной для архитектуры 20 века чертой – в них присутствовало понимание пространства как четырехмерной структуры, учитывающей одним из своих измерений время.
Слайд 17Производственное здание Bacardi Rum Factory
В связи с простотой уравнения теория мембран
для гипаров имеет простое решение.
Оно было получено в начале 30-х годов XX в. инженером французской государственной железной дороги Ф. Аймондом,
Трамвайный парк.(Липецк)
Слайд 18Феликс Кандела сказал однажды: «Я раскрыл свои зонтики над половиной стран!
Больше, чем над половиной».
Именно зонтичная форма свода, состоящая из крыши на опорах и четырехсторонней бетонной оболочки, является самой знаменитой структурной формой, разработанной этим талантливым архитектором.
Слайд 19Цель: с помощью редактора Excel
построить гипар
График гиперболического параболоида описывается уравнением
Z=(x/a)2-(y/b)2
Слайд 20В ячейках А1 и В2 находятся параметры а и в, соответственно.
Для гиперболического параболоида а=4 и в=5,
Область изменения независимых переменны x и y - квадрат (-5;5) x (-5;5).
Переменные принимают значения с шагом 0,5:
Область изменения независимых переменны x и y - квадрат (-5;5) x (-5;5).
Переменные принимают значения с шагом 0,5:
Слайд 21Вводим значения в таблицу Excel:
В ячейках А1 и В2 вводим
а=4 и в=5
В В2 ввести -5, в А3 ввести -5
Слайд 23
Для получения ряда данных, вычисляемых по формуле гиперболического параболоида,
выполните следующие действия:
Введите в ячейку B2 число -5 и после ввода вернитесь в ячейку B2.
Введите в ячейку B2 число -5 и после ввода вернитесь в ячейку B2.
Слайд 24 Выполните команду Редактирование , Заполнить, Прогрессия(вкладка Главная). В диалоговом
окне Прогрессии выберите режим по строкам и тип арифметическая, введите шаг 0,5 и предельное значение 5.
Слайд 27Мы ввели область изменения переменной х.
Аналогичные действия выполните для определения
ввода области изменения переменной у с тем отличием, что в окне Прогрессии надо выбрать режим по столбцам, а первое значение ввести в ячейку А3.
Слайд 29 Теперь введем формулы для вычисления значений функции. для этого в
ячейку В3 в введите формулу
= (В$2/$А$1)^2-($A3/$B$1)^2
= (В$2/$А$1)^2-($A3/$B$1)^2
Слайд 30Далее распространите эту формулу на всю строку, расположенную под строкой со
значением переменной х. После этого, не отменяя выделение, установите указатель мыши в точку в правом нижнем углу последней выделенной ячейки в строке 3.
Затем распространите выделенные в ячейках формулы на все строки, соответствующие значениям переменной у в столбце А.
Затем распространите выделенные в ячейках формулы на все строки, соответствующие значениям переменной у в столбце А.
Слайд 32Постройте трехмерную диаграмму типа "Поверхность" по областям А2:V23 на отдельном листе
в черно-белом варианте с необходимым оформлением.
Вставка – диаграмма - другие диаграммы - поверхность
Вставка – диаграмма - другие диаграммы - поверхность
Слайд 33 Должен получиться график показанный ниже.
Диаграммы необходимо полностью оформить, т.е.
должны быть обозначены все оси, сетка, иметься все надписи и подписи и т.п.
Слайд 35Выставочный комплекс Экспо 67 в Монреале, архитектор Отто Фрай
Аэропорт Даллеса архитектор
Ээро Сааринен
Мюнхенский олимпийский парк (крыши - архитектор Отто Фрай,)
Примеры архитектурных сооружений с крышами в форме гипар
Слайд 36
Феликс Кандела
«Вместо воспитания
безудержной фантазии и изобретательства
мы должны заставлять
наших студентов постоянно осознавать
опасность, кроющуюся в физических ограничениях. [...]
опасность, кроющуюся в физических ограничениях. [...]
Слайд 37Феликс Кандела «Я начал изучать архитектуру совершенно случайно, без всякой веры в
свои способности. Должно быть, именно эта внутренняя неуверенность и заставила меня пройти через все сложности изучения структурного анализа и сопротивления материалов».
