- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике по теме Рекурсия. Задание №11 в ЕГЭ по информатике
Содержание
- 1. Презентация по информатике по теме Рекурсия. Задание №11 в ЕГЭ по информатике
- 2. Рекурсия – это способ определения множества объектов
- 3. Рекурсия в лингвистике Способность языка порождать вложенные предложения и конструкции.Вот дом,Который построил Джек.А
- 4. Рекурсия в физикеКлассическим примером бесконечной рекурсии являются
- 5. Рекурсивная процедура (функция)* – это процедура (функция),
- 6. ЕГЭ №11. Рекурсивные алгоритмыБазовый уровеньВремя - 5 мин.
- 7. Виды заданий:Значение функции«Звездочки»Сумма напечатанных чиселПоследовательность чисел
- 8. Задание № 1Алгоритм вычисления значения функции F(n),
- 9. Задание № 2Алгоритм вычисления значений функций F(n)
- 10. F(1) = 1; G(1) = 1; F(n)
- 11. Задание № 3Записаны две рекурсивные функции (процедуры):
- 12. Задание № 4Записан рекурсивный алгоритм F.procedure F(n:
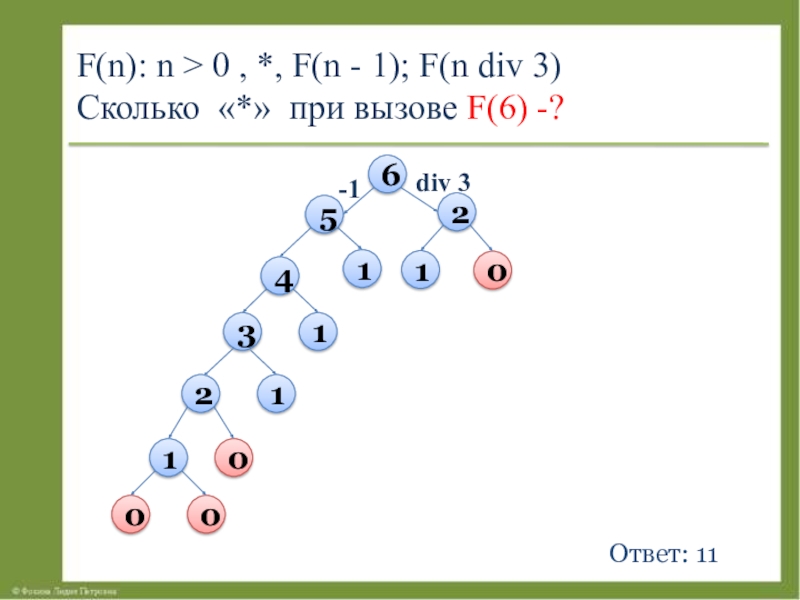
- 13. F(n): n > 0 , *, F(n
- 14. Задание № 5Сколько символов "звёздочка" будет выведено
- 15. Задание № 6.1Чему равна сумма всех чисел,
- 16. Задание № 6.2Чему равна сумма всех чисел,
- 17. Задание № 7procedure F(n: integer);begin if
- 18. Что выведет программа при вызове F(5)? procedure
Слайд 1«Рекурсия. Задания типа 11 в ЕГЭ по информатике»
Беспрозванных Любовь Сергеевна
Вуйкив
Слайд 2Рекурсия – это способ определения множества объектов через само это множество
Слайд 3Рекурсия в лингвистике
Способность языка порождать вложенные предложения и конструкции.
Вот дом,
Который построил Джек.
А это пшеница,
Которая в тёмном чулане
В доме,
Который построил Джек.
А это весёлая птица-синица,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
Вот кот,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
Вот пёс без хвоста,
Который за шиворот треплет кота,
…
Самуил Маршак
Базовое предложение
Слайд 4Рекурсия в физике
Классическим примером бесконечной рекурсии являются два поставленные друг напротив
Слайд 5Рекурсивная процедура (функция)* – это процедура (функция), которая вызывает сама себя
Чтобы определить рекурсию, нужно:
задать условие остановки рекурсии (базовый случай или несколько базовых случаев)
рекуррентную формулу.
* К.Ю. Поляков
Слайд 8Задание № 1
Алгоритм вычисления значения функции F(n), где n — натуральное
F(1) = 1;
F(2) = 1;
F(n) = F(n - 2) * (n - 1), при n > 2.
Чему равно значение функции F(7)?
F(7) = F(5) * 6 =
F(5) = F(3) * 4 =
F(3) = F(1) * 2 =
Ответ: 48
2
8
48
Слайд 9Задание № 2
Алгоритм вычисления значений функций F(n) и G(n), где n
F(1) = 1;
G(1) = 1;
F(n) = 2*F(n–1) – G(n–1),
G(n) = 2*F(n–1) + G(n–1), при n >=2
Чему равно значение величины F(5)-G(5)?
Слайд 10F(1) = 1; G(1) = 1; F(n) = 2*F(n–1) – G(n–1), G(n)
F(5) = 2*F(4)-G(4)=-17
F(4) = 2*F(3)-G(3)=-7
F(3) = 2*F(2)-G(2)=-1
F(2) = 2*F(1)-G(1)=1
Ответ: -6
G(5) = 2*F(4)+G(4)=-11
G(4) = 2*F(3)+G(3)=3
G(3) = 2*F(2)+G(2)=5
G(2) = 2*F(1)+G(1)=3
F(5)-G(5) =-17-(-11)=-17+11=-6
Слайд 11Задание № 3
Записаны две рекурсивные функции (процедуры): F и G.
procedure F(n:
procedure G(n: integer); forward;
procedure F(n: integer); begin if n > 0 then G(n - 1); end;
procedure G(n: integer); begin writeln('*'); if n > 1 then F(n - 3); end;
Сколько символов «звёздочка» будет напечатано на экране при выполнении вызова F(11)?
F(11) G(10) F(7) G(6) F(3) G(2) F(-1)
Ответ: 3
Слайд 12Задание № 4
Записан рекурсивный алгоритм F.
procedure F(n: integer);
begin
if n > 0
begin
writeln('*');
F(n - 1);
F(n div 3)
end
end
Сколько символов «звёздочка» будет напечатано на экране при выполнении вызова F(6)?
Слайд 14Задание № 5
Сколько символов "звёздочка" будет выведено на экран при вызове
Ответ: 10
Procedure F(n: integer);
begin
if n mod 2 = 0 then
writeln('*')
else
writeln('**');
if n > 0 then
F(n - 1);
end;
Слайд 15Задание № 6.1
Чему равна сумма всех чисел, напечатанных на экране при
Ответ: 11
procedure F(n: integer);
begin
writeln(n);
if n > 0 then
begin
F(n - 1);
F(n - 3)
end
end
Решение:
1 способ.
S(n) - сумма чисел напечатанных при вызове F(n).
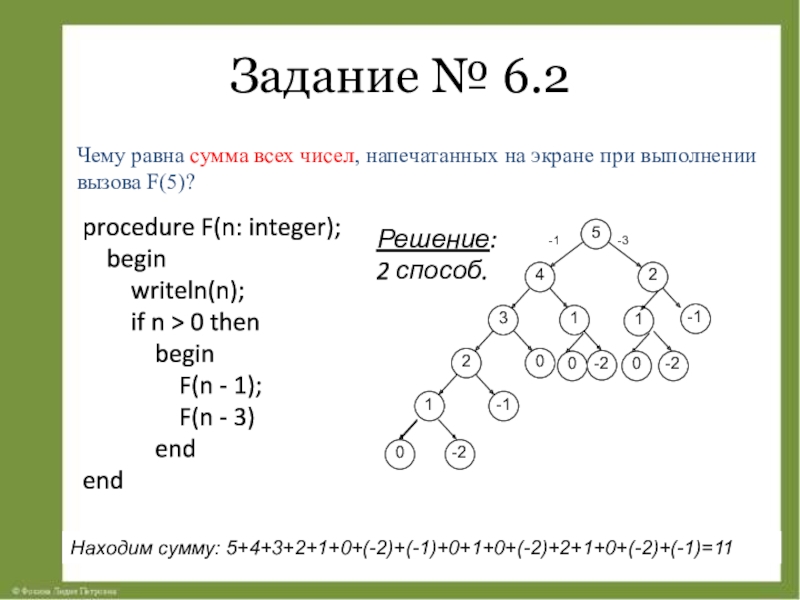
Слайд 16Задание № 6.2
Чему равна сумма всех чисел, напечатанных на экране при
procedure F(n: integer);
begin
writeln(n);
if n > 0 then
begin
F(n - 1);
F(n - 3)
end
end
Решение:
2 способ.
Находим сумму: 5+4+3+2+1+0+(-2)+(-1)+0+1+0+(-2)+2+1+0+(-2)+(-1)=11
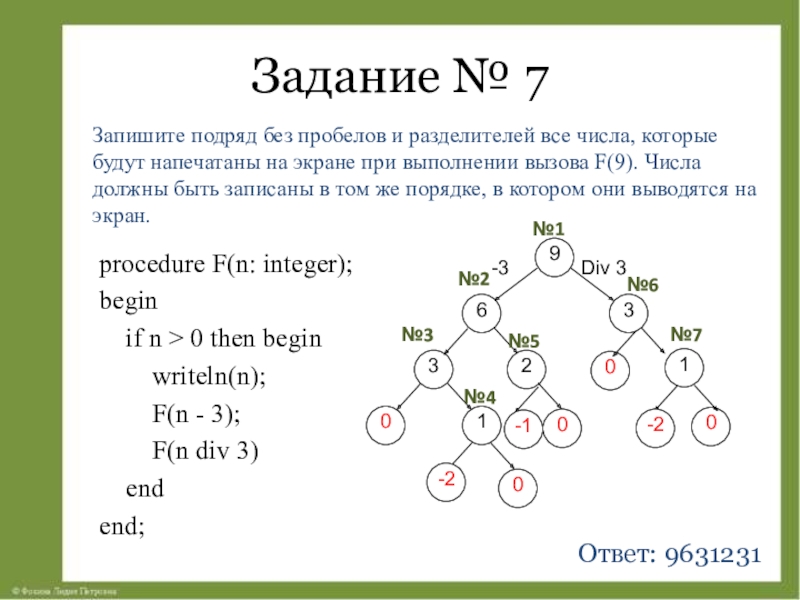
Слайд 17Задание № 7
procedure F(n: integer);
begin
if n > 0 then
writeln(n);
F(n - 3);
F(n div 3)
end
end;
Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(9). Числа должны быть записаны в том же порядке, в котором они выводятся на экран.
Ответ: 9631231
№1
№2
№3
№4
№5
№6
№7
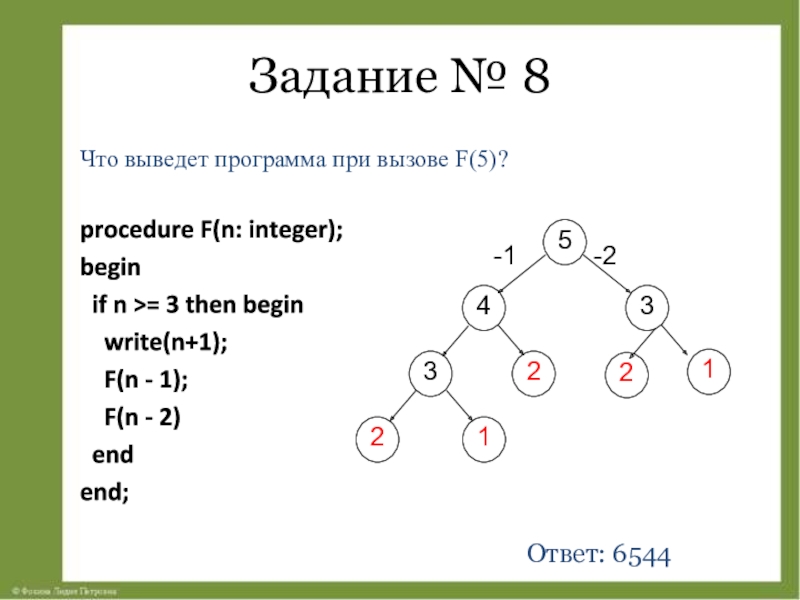
Слайд 18Что выведет программа при вызове F(5)?
procedure F(n: integer);
begin
if
write(n+1);
F(n - 1);
F(n - 2)
end
end;
Задание № 8
Ответ: 6544