- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике по теме Модели оптимального планирования
Содержание
- 1. Презентация по информатике по теме Модели оптимального планирования
- 2. Слайд 2
- 3. С древних времен человека интересовали задачи связанные
- 4. Школьный кондитерский цех готовит пирожки и пирожные.
- 5. • х — дневной план выпуска пирожков;
- 6. А теперь перейдем к формализации стратегической цели:
- 7. А теперь перейдем к формализации стратегической цели:
- 8. Система написанных неравенств представляется на координатной плоскости
Слайд 3С древних времен человека интересовали задачи связанные с отысканием наименьших и
В XX веке при огромном размахе производства и осознании ограниченности ресурсов Земли стала актуальной задача оптимального использования энергии, материалов, рабочего времени.
Многие задачи сводятся к отысканию наименьшего или наибольшего значения некоторой функции, которую принято называть целевой функцией или критерием качества.
Задачи оптимизации могут быть успешно решены с помощью компьютера. Они решаются по обычной схеме: - составление математической модели, - компьютерной модели - исследование модели.
ОПТИМИЗАЦИОННЫЕ ЗАДАЧИ
Слайд 4Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности -
Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха.
ПРИМЕР ЗАДАЧИ
Слайд 5• х — дневной план выпуска пирожков; • у — дневной
Ресурсы производства: • длительность рабочего дня — 8 часов; • вместимость складского помещения — 700 мест.
Предполагается, что другие ресурсы (сырье, электроэнергия и пр.) не ограничены.
Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада.
ПРИМЕР ЗАДАЧИ
На 1 пирожок - в 4 раза больше времени.
tx + 4ty = (х + 4y)t.
Ограничение - не больше рабочего дня – 8*60.
(х + 4y)t ≤ 8 • 60, или (х + 4y)t ≤ 480.
На один пирожок тратится 480/1000 = 0,48 мин
(х + 4у) • 0,48 ≤ 480. или х + 4у ≤ 1000.
Имеется ограничение на общее число изделий
х + у ≤ 700.
Слайд 6А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка
rх + 2rу = r(х + 2у).
Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:
F(x, у) = r(х + 2у).
Она называется целевой функцией.
Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять f(x, у) = х + 2у.
Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств и придающих максимальное значение целевой функции.
ЦЕЛЕВАЯ ФУНКЦИЯ
Слайд 7А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка
rх + 2rу = r(х + 2у).
Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:
F(x, у) = r(х + 2у). Она называется целевой функцией.
Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять f(x, у) = х + 2у.
Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств и придающих максимальное значение целевой функции.
ЦЕЛЕВАЯ ФУНКЦИЯ
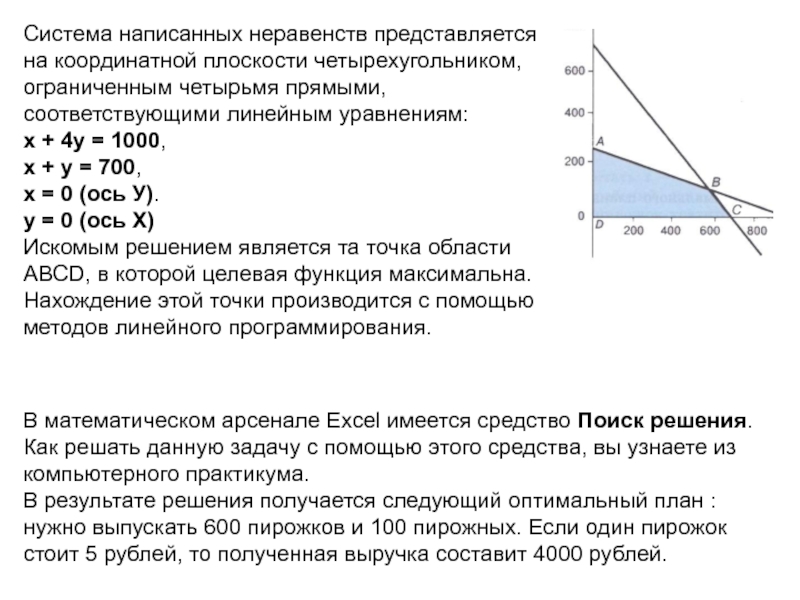
Слайд 8Система написанных неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми,
х + 4у = 1000,
х + у = 700,
х = 0 (ось У).
у = 0 (ось X)
Искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.
В математическом арсенале Excel имеется средство Поиск решения. Как решать данную задачу с помощью этого средства, вы узнаете из компьютерного практикума.
В результате решения получается следующий оптимальный план : нужно выпускать 600 пирожков и 100 пирожных. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.