- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике: Основы логики
Содержание
- 1. Презентация по информатике: Основы логики
- 2. Конъюнкция, логическое умножение (and - и);Дизъюнкция, логическое
- 3. К о н ъ ю н к
- 4. Д и з ъ ю н к
- 5. И н в е р с и
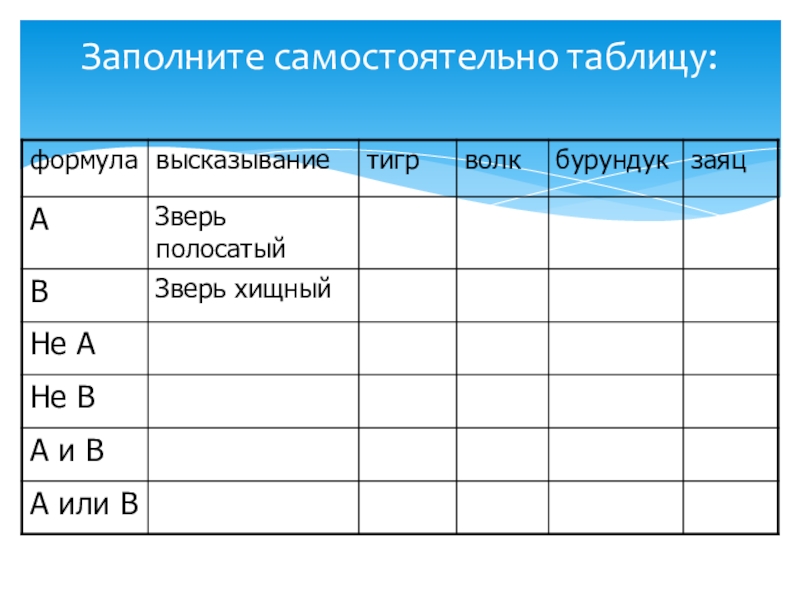
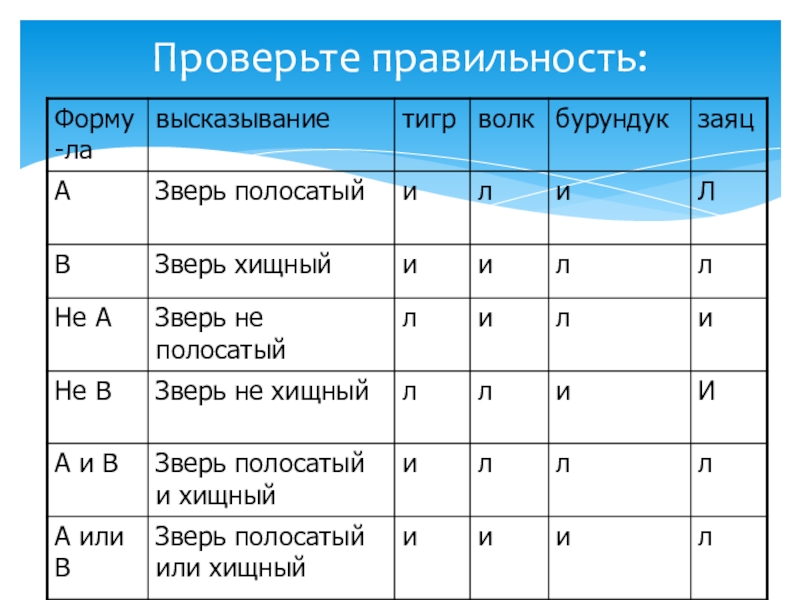
- 6. Заполните самостоятельно таблицу:
- 7. Проверьте правильность:
- 8. Импликация F(A,B)= A → BИмпликацией двух высказываний
- 9. Эквивалентность F(A,B)= A ~ BСоединение двух простых
- 10. Эквивалентность
- 11. Это булевы константы и
- 12. 1. не 0 = 1, не
- 13. 5. Х or неХ=1, Х · неХ=06.
- 14. Для самостоятельного изучения:Закон де Морганане (А или
- 15. Большинство логических задач решается по
Слайд 2Конъюнкция, логическое умножение (and - и);
Дизъюнкция, логическое сложение (or - или);
Инверсия,
Импликация ( - следование)(если высказывание истинно, то…)
Эквивалентность (~ - тогда и только тогда, когда)
Высказывания в алгебре логики обозначаются латинскими буквами
Основные логические операции:
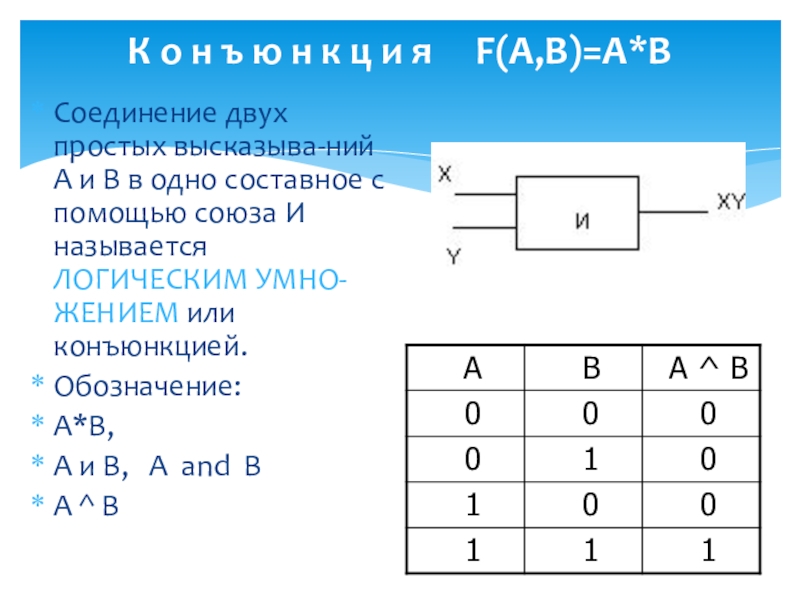
Слайд 3К о н ъ ю н к ц и я
Соединение двух простых высказыва-ний А и В в одно составное с помощью союза И называется ЛОГИЧЕСКИМ УМНО-ЖЕНИЕМ или конъюнкцией.
Обозначение:
А*В,
А и В, А and В
А ^ В
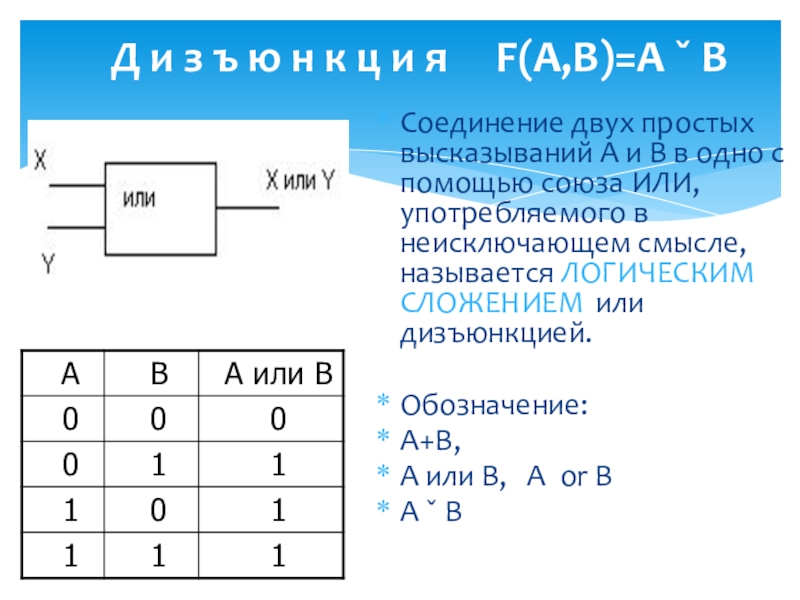
Слайд 4Д и з ъ ю н к ц и я
Соединение двух простых высказываний А и В в одно с помощью союза ИЛИ, употребляемого в неисключающем смысле, называется ЛОГИЧЕСКИМ СЛОЖЕНИЕМ или дизъюнкцией.
Обозначение:
А+В,
А или В, А or В
А ˇ В
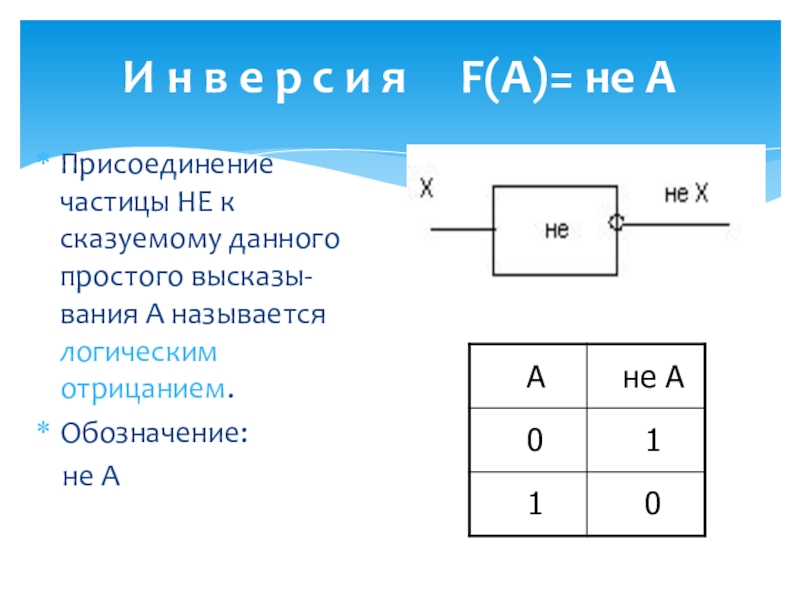
Слайд 5И н в е р с и я F(A)=
Присоединение частицы НЕ к сказуемому данного простого высказы-вания А называется логическим отрицанием.
Обозначение:
не А
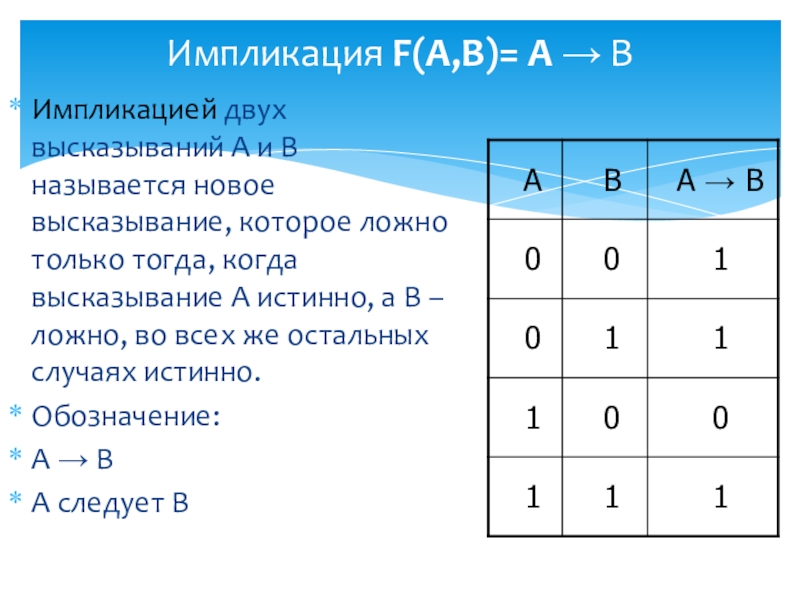
Слайд 8Импликация F(A,B)= A → B
Импликацией двух высказываний А и В называется
Обозначение:
А → В
А следует В
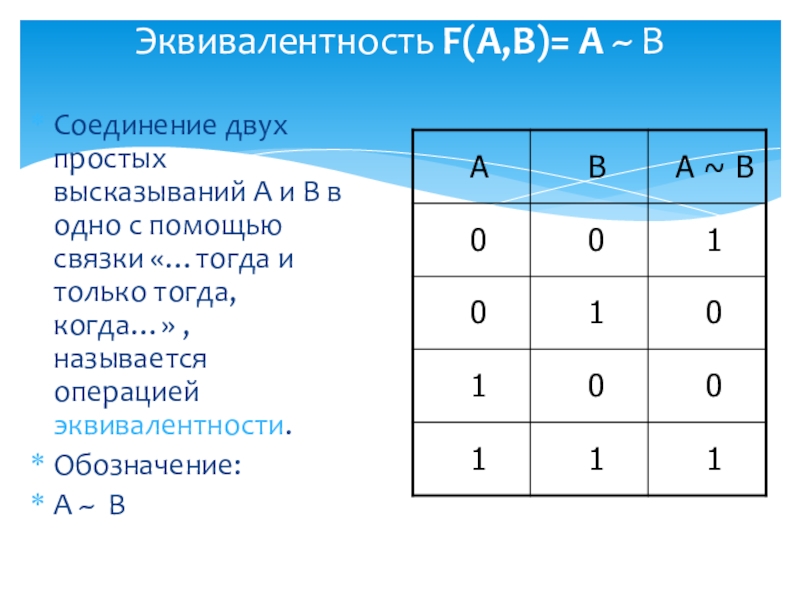
Слайд 9Эквивалентность F(A,B)= A ~ B
Соединение двух простых высказываний А и В
Обозначение:
А ~ В
Слайд 11 Это булевы константы и переменные, связанные логическими операциями
СТАРШИНСТВО ЛОГИЧЕСКИХ ОПЕРАЦИЙ :
Инверсия
Конъюнкция
Дизъюнкция
Для изменения порядка действий
используются скобки.
Логические (булевы) выражения -
Слайд 121. не 0 = 1, не 1 = 0
2.
3. Х or 1=1, Х · 0=0
4. Х or Х=Х, Х · Х=Х – з-н идемпотентности -
основной закон алгебры Буля, в соответствии с
которым исключаются все коэффициенты и
показатели степеней.
А+А+А+А=А
А·А·А=А
Теоремы алгебры логики
Слайд 135. Х or неХ=1, Х · неХ=0
6. не(неХ) = Х
отрицания
7. Х or Y = Y or X, X · Y = Y · X
коммутативный закон
8. X or X · Y=X, X ·(X or Y)=X - закон
поглощения
Теоремы алгебры логики
Слайд 14Для самостоятельного изучения:
Закон де Моргана
не (А или В) = (не А)
Ассоциативный закон
Сочетательный (ассоциативный) закон: (А или В) или С = А или (В или С) (А и В) и С = А и (В и С)
Дистрибутивный закон
Распределительный (дистрибутивный) закон: (А и В) или С = (А или С) и (В или С) (А или В) и С = (А и С) или (А и В)
Теоремы алгебры логики
Слайд 15 Большинство логических задач решается по следующему алгоритму:
изучение условия задачи
обозначение
составление логических выражений, удовлетворяющих всем требованиям задачи
объединение их в одно выражение
Вычисление всех значений этого логического выражения
проверка полученного решения по условию задачи
Алгоритмы решения логических задач: