- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Нормальный алгоритм Маркова
Содержание
- 1. Презентация по информатике Нормальный алгоритм Маркова
- 2. меню Андрей Андреевич МарковНормальный алгоритмБиографияНаучный вклад и награды Пример 1ОписаниеВозможности нормальных алгоритмовПример 2
- 3. Марков, Андрей Андреевич (младший) Дата рождения :9
- 4. БиографияАндре́й Андре́евич Ма́рков — советский математик, сын
- 5. Научный вкладОсновные труды — по теории динамических
- 6. Норма́льный алгори́тм (алгори́фм) Ма́ркова—— один из стандартных
- 7. ОписаниеС М
- 8. МН
- 9. ПримерС М
- 10. Н М
- 11. Возможности нормальных алгоритмовПрежде всего рассмотрим возможности реализации
- 12. Рассмотрим простейшую операцию увеличения десятичного числа на
- 13. Таким образом, мы получаем следующий НАМ увеличения
Слайд 2меню
Андрей Андреевич Марков
Нормальный алгоритм
Биография
Научный вклад и награды
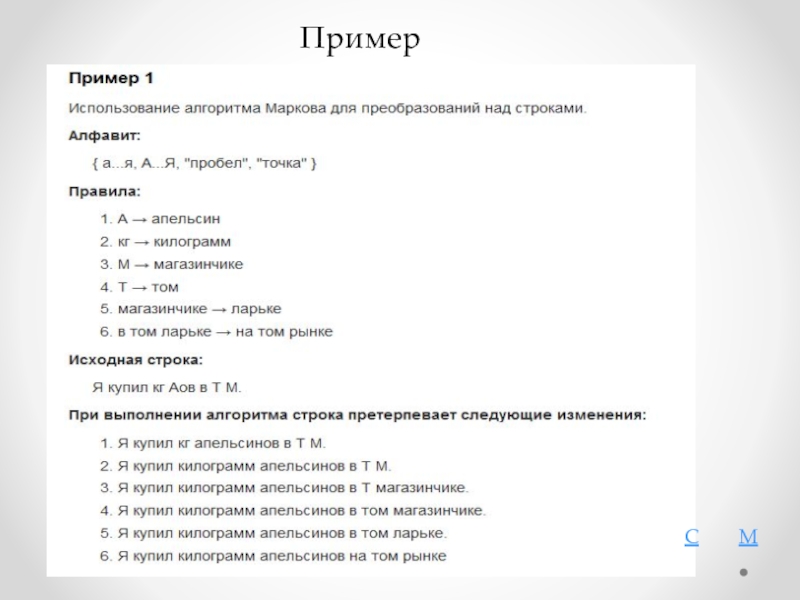
Пример 1
Описание
Возможности нормальных
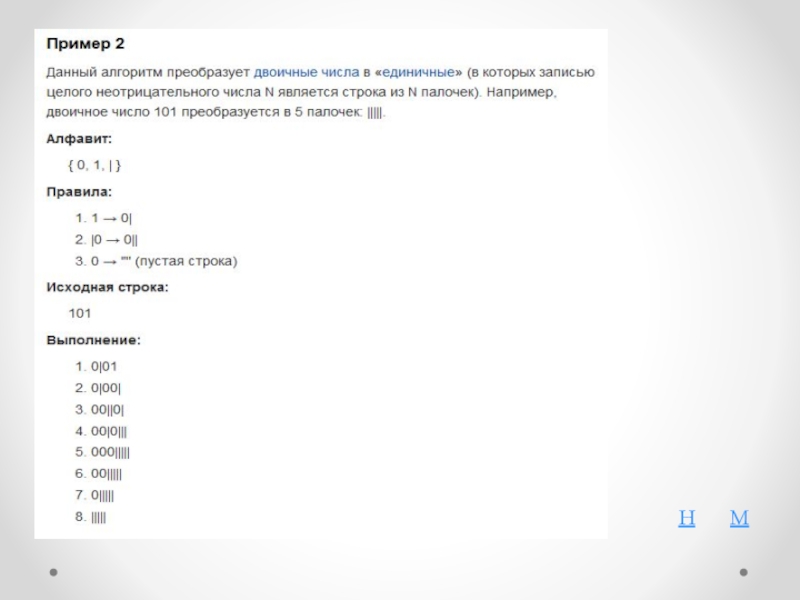
Пример 2
Слайд 3Марков, Андрей Андреевич (младший)
Дата рождения :9 (22) сентября 1903
Место рождения :
Дата смерти :11 октября 1979 (76 лет)
Научная сфера :математика
Место работы :ЛГУ; МГУ; ВЦ АН СССР;
Математический институт им. В. А. Стеклова АН СССР
Учёная степень : доктор физико-математических наук
Известен как : основоположник советской школы конструктивной математики
М
Слайд 4Биография
Андре́й Андре́евич Ма́рков — советский математик, сын известного русского математика А.
Окончил Восьмую Петроградскую гимназию в 1919 году; Ленинградский государственный университет в 1924 году; аспирантуру в Астрономическом институте в Ленинграде в 1928 году.
Учёная степень доктора физико-математических наук присвоена без защиты диссертации в 1935 году. Член-корреспондент АН СССР с 1953 года, в том же году вступил в КПСС.
В 1933—1955 годах работал в Ленинградском университете (с 1936 г. — профессор): с 1936 по 1942 год и с 1943 по 1953 год — заведующий кафедрой геометрии. До июля 1942 года находился в блокадном Ленинграде.
С 1959 по 1979 год — заведующий кафедрой математической логики Московского государственного университета.
Одновременно в 1939—1972 работал в Математическом институте имени Стеклова АН СССР.
В 1950-х годах создал в Вычислительном Центре АН СССР лабораторию математической логики и структуры машин, которой руководил около двадцати лет.
М
Слайд 5Научный вклад
Основные труды — по теории динамических систем, топологии, топологической алгебре,
Доказал неразрешимость проблемы равенства в ассоциативных системах (1947), проблемы гомеоморфии в топологии (1958), создал школу конструктивной математики и логики в СССР, автор понятия нормального алгоритма.
Награды
Орден «Знак Почёта» (1945)
Орден Ленина (1954)
Орден Трудового Красного Знамени (1963)
Медаль «За доблестный труд в Великой Отечественной войне 1941—1945 гг.» (1945)
Медаль «За оборону Ленинграда» (1946)
Премия имени П. Л. Чебышёва АН СССР (1969)
М
Слайд 6Норма́льный алгори́тм (алгори́фм) Ма́ркова—— один из стандартных способов формального определения понятия
Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ является Тьюринг-полным языком, что делает его по выразительной силе эквивалентным машине Тьюринга и, следовательно, современным языкам программирования. На основе НАМ был создан функциональный язык программирования Рефал.
М
Слайд 11Возможности нормальных алгоритмов
Прежде всего рассмотрим возможности реализации арифметических операций с помощью
М
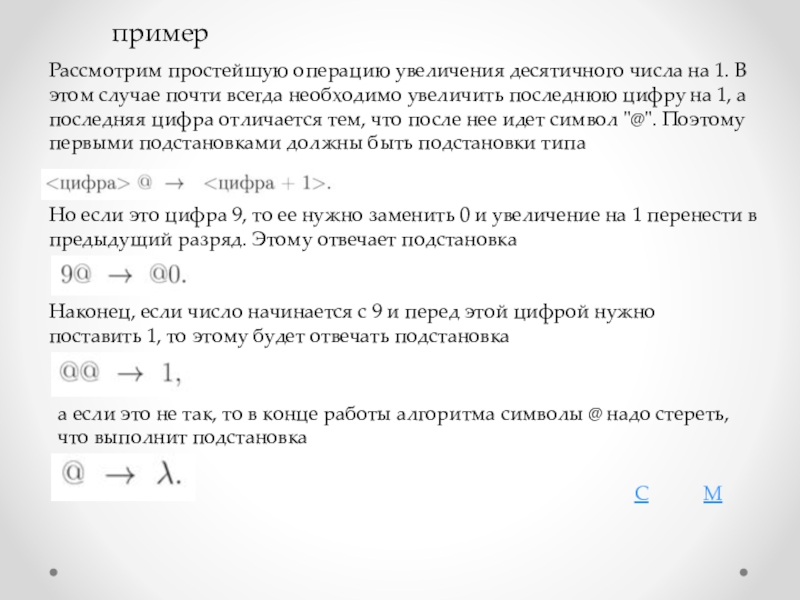
Слайд 12Рассмотрим простейшую операцию увеличения десятичного числа на 1. В этом случае
пример
Но если это цифра 9, то ее нужно заменить 0 и увеличение на 1 перенести в предыдущий разряд. Этому отвечает подстановка
Наконец, если число начинается с 9 и перед этой цифрой нужно поставить 1, то этому будет отвечать подстановка
а если это не так, то в конце работы алгоритма символы @ надо стереть, что выполнит подстановка
С М
Слайд 13Таким образом, мы получаем следующий НАМ увеличения десятичного числа на 1:
Приведем
Аналогичным образом разрабатывается нормальный алгоритм Маркова для уменьшения числа на 1
Н М