- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Введение в теорию графов (11 класс)
Содержание
- 1. Презентация по информатике на тему Введение в теорию графов (11 класс)
- 2. ЗАДАЧА: Для игры в локальной сети необходимо
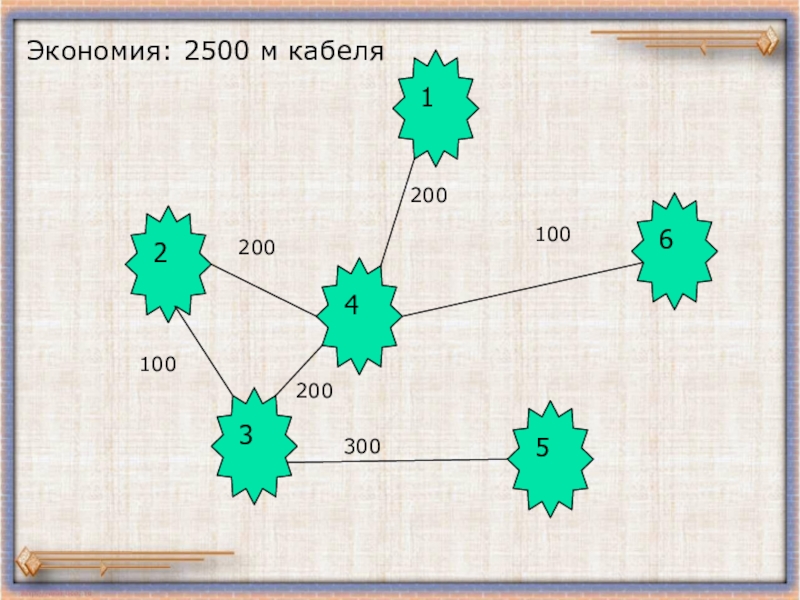
- 3. 145362100200100200300200Экономия: 2500 м кабеля
- 4. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВv5v2v3v1v4R34R45R15R23R35R34R12R14V-ВЕРШИНЫ (населенные пункты, компьютеры,
- 5. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВv5v2v3v1v4R34R45R15R23R35R34R12R14количество вершин и количество
- 6. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВv5v2v3v1v4R34R45R15R23R35R34R12R14МАРШРУТ ГРАФА –ПОСЛЕДОВАТЕЛЬНОСТЬ ЧЕРЕДУЮЩИХСЯ
- 7. ТИПЫ ГРАФОВ
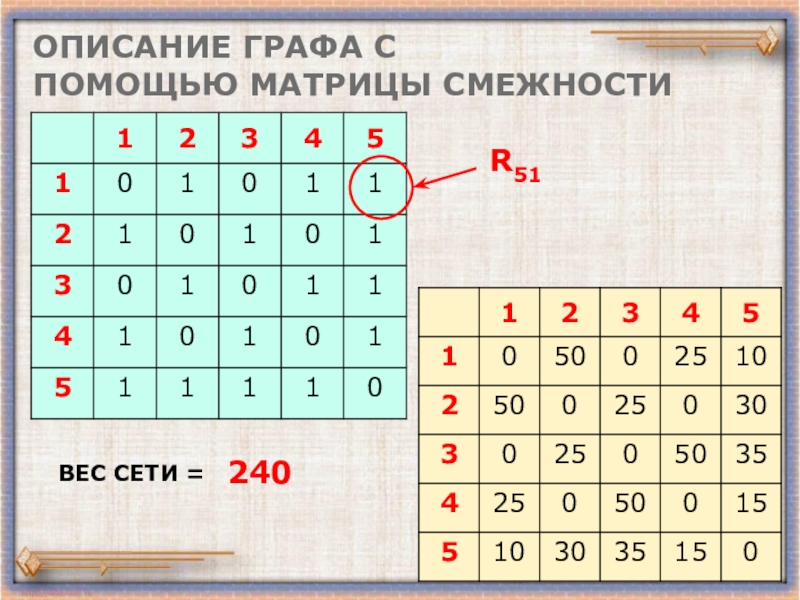
- 8. ОПИСАНИЕ ГРАФА С ПОМОЩЬЮ МАТРИЦЫ СМЕЖНОСТИR51ВЕС СЕТИ =240
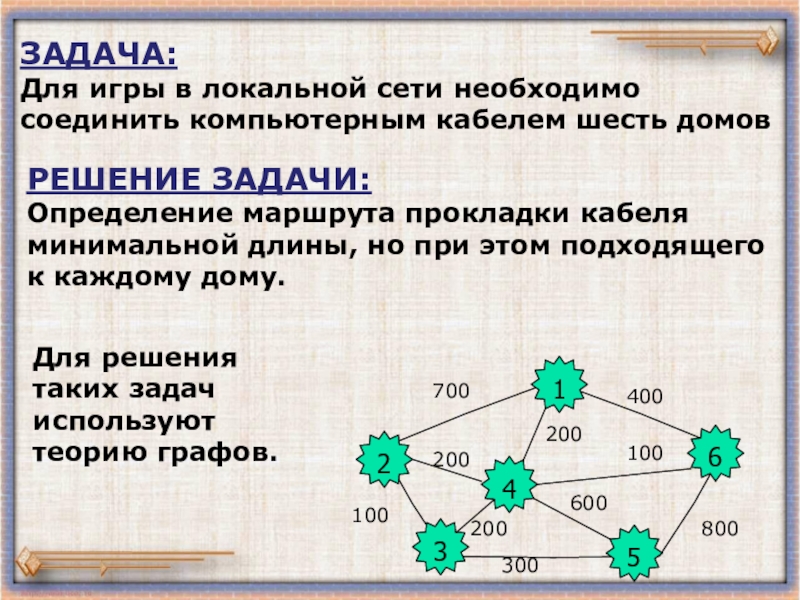
Слайд 2ЗАДАЧА:
Для игры в локальной сети необходимо соединить компьютерным кабелем шесть
РЕШЕНИЕ ЗАДАЧИ:
Определение маршрута прокладки кабеля минимальной длины, но при этом подходящего к каждому дому.
Для решения таких задач используют теорию графов.
1
4
5
3
6
2
400
700
100
200
100
800
200
300
200
600
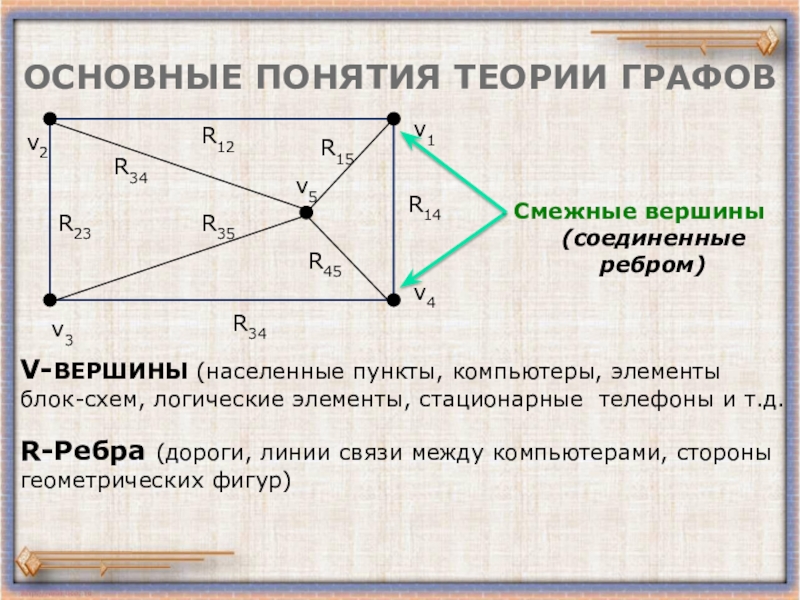
Слайд 4ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ
v5
v2
v3
v1
v4
R34
R45
R15
R23
R35
R34
R12
R14
V-ВЕРШИНЫ (населенные пункты, компьютеры, элементы блок-схем, логические элементы,
R-Ребра (дороги, линии связи между компьютерами, стороны геометрических фигур)
Смежные вершины
(соединенные ребром)
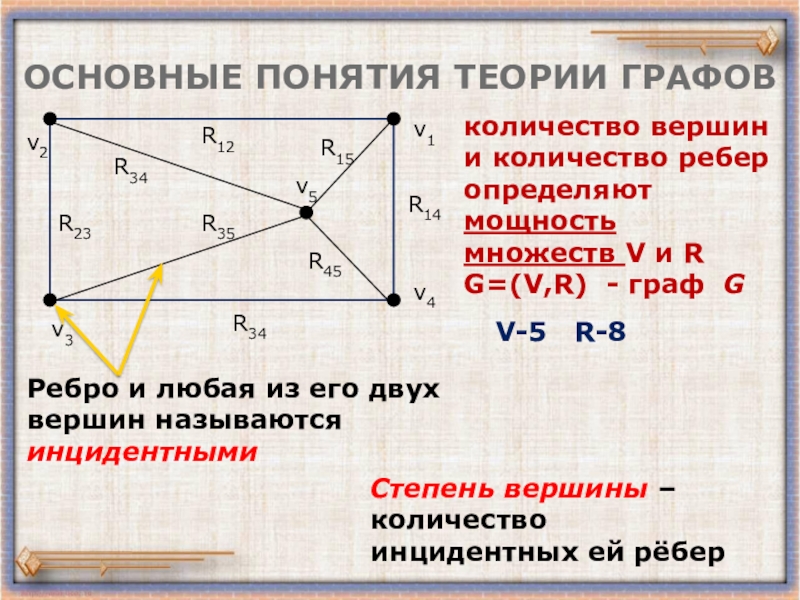
Слайд 5ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ
v5
v2
v3
v1
v4
R34
R45
R15
R23
R35
R34
R12
R14
количество вершин и количество ребер определяют мощность множеств
G=(V,R) - граф G
Ребро и любая из его двух
вершин называются инцидентными
Степень вершины –
количество инцидентных ей рёбер
V-5 R-8
Слайд 6ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ
v5
v2
v3
v1
v4
R34
R45
R15
R23
R35
R34
R12
R14
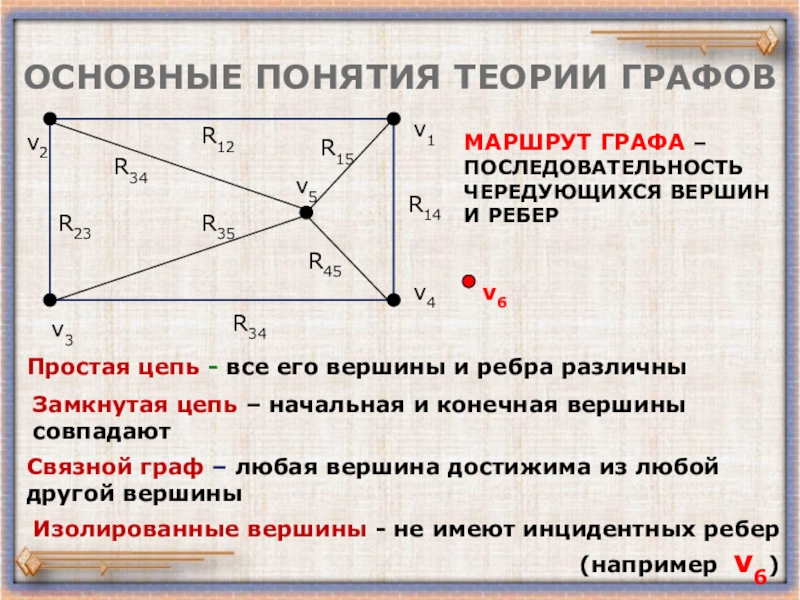
МАРШРУТ ГРАФА –ПОСЛЕДОВАТЕЛЬНОСТЬ ЧЕРЕДУЮЩИХСЯ ВЕРШИН И РЕБЕР
Простая цепь
Замкнутая цепь – начальная и конечная вершины совпадают
Связной граф – любая вершина достижима из любой другой вершины
Изолированные вершины - не имеют инцидентных ребер (например v6)