- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Системы счисления
Содержание
- 1. Презентация по информатике на тему Системы счисления
- 2. Давайте обсудим… Обучение я закончил в 44
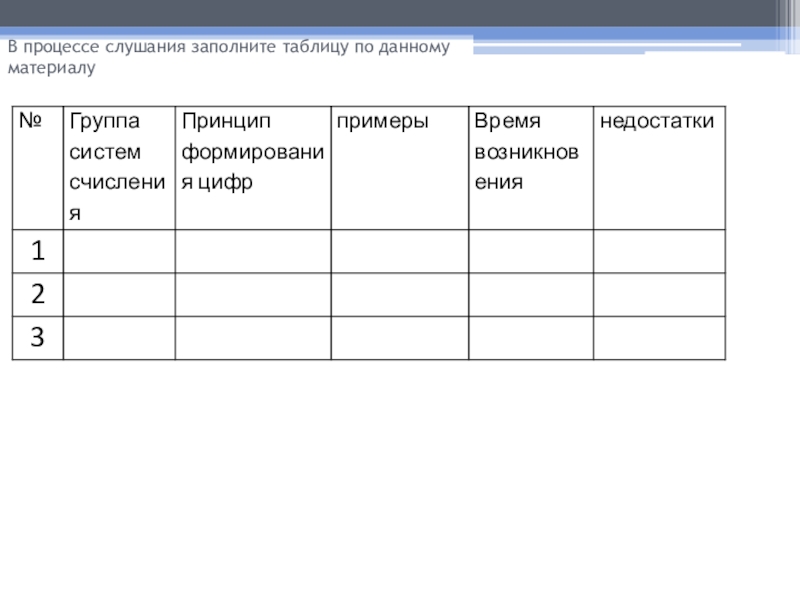
- 3. В процессе слушания заполните таблицу по данному материалу
- 4. Слайд 4
- 5. Системы счисленияОбщие понятияЭкскурс в прошлое и настоящее позиционных с/с.Таблица переводовПравила математикиПравила переводов
- 6. Общие понятияСистема счисления - это алфавит определенных
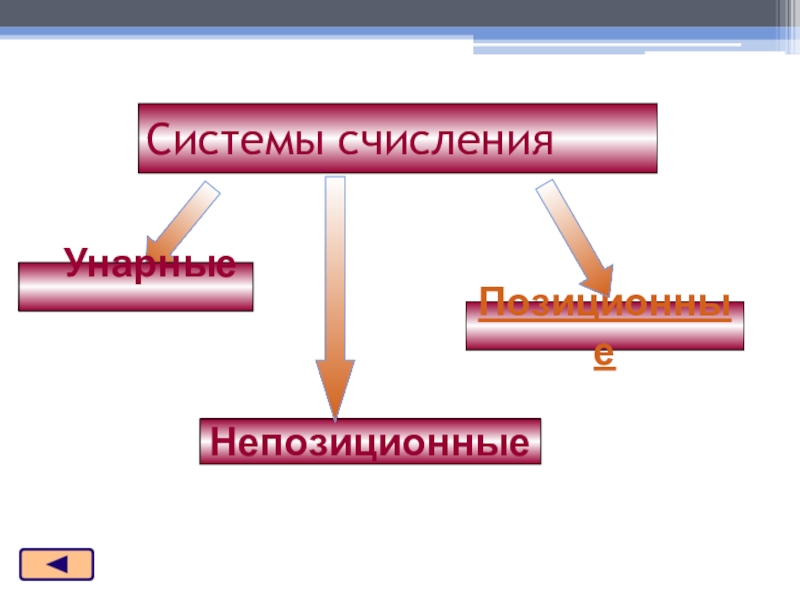
- 7. Системы счисленияПозиционныеНепозиционные Унарные
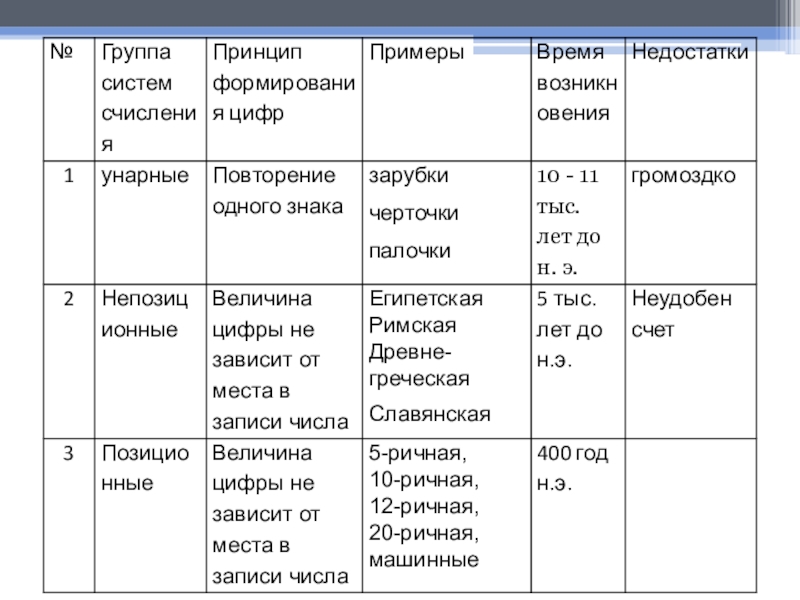
- 8. Унарные системыЧисло образуется путем повторения одного знака, символизирующего единицу.Примеры:зарубкичерточкипалочки10 - 11 тыс. лет до н. э.
- 9. Непозиционные системы -системы счисления, в которых каждой
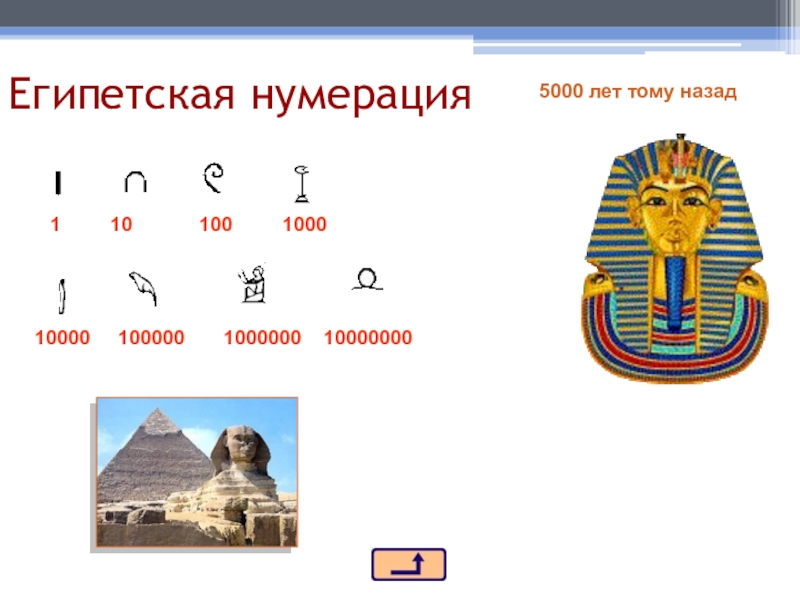
- 10. Египетская нумерация1 10
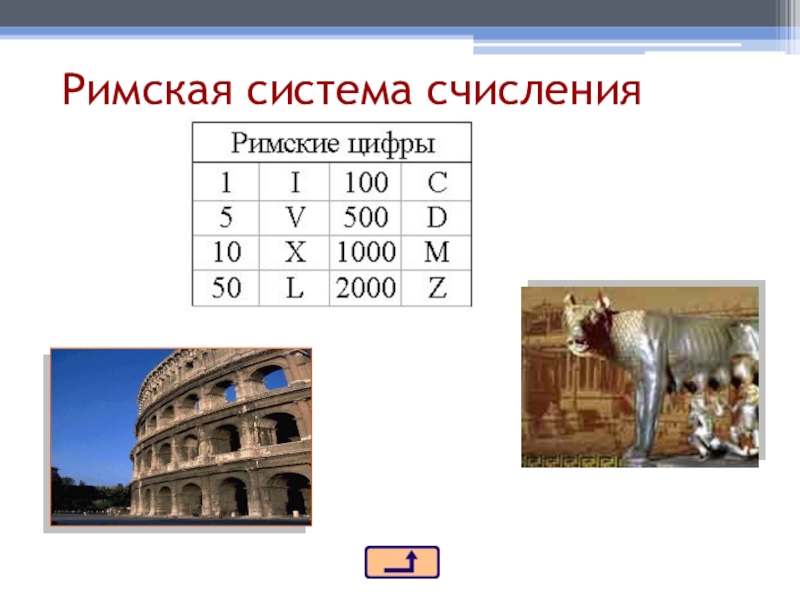
- 11. Римская система счисления
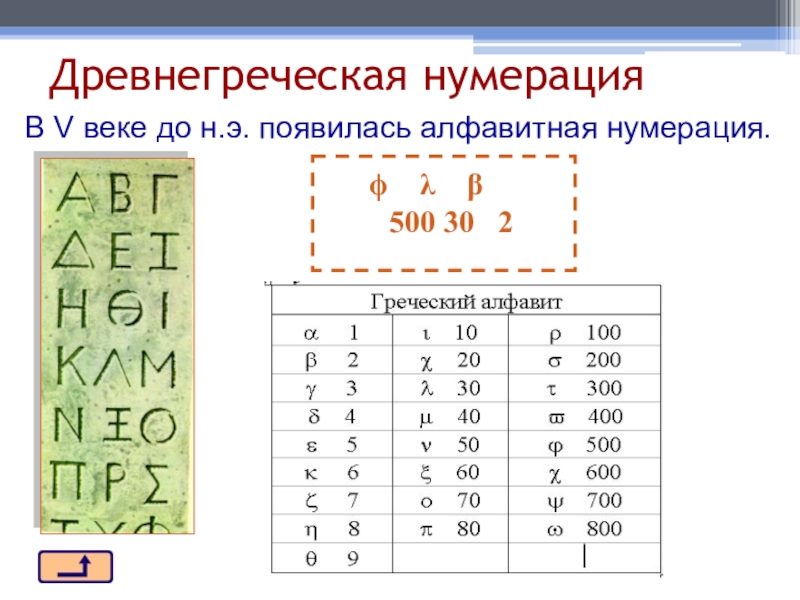
- 12. Древнегреческая нумерацияВ V веке до н.э. появилась алфавитная нумерация.
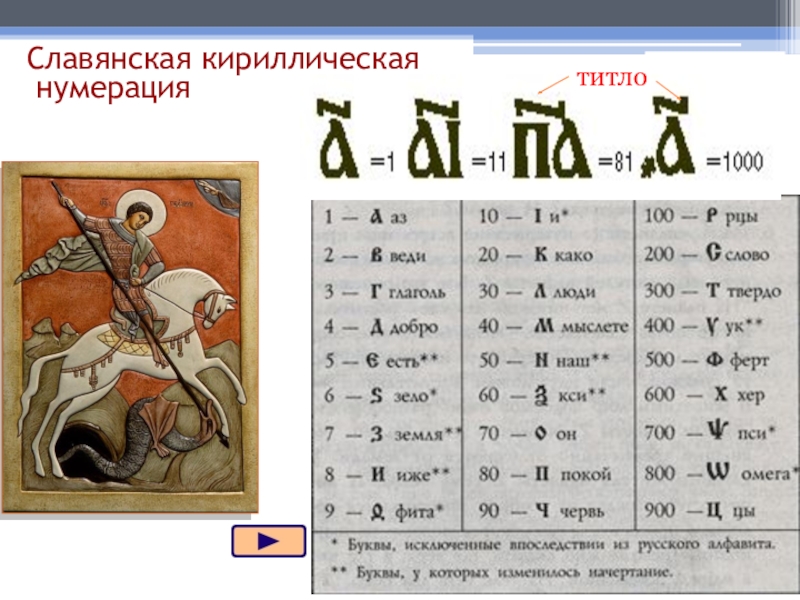
- 13. Славянская кириллическая нумерациятитло
- 14. - 1000- 7000- 2000- 10000- 20000- 50000(Тьма)- 200000- 100000(Легионы)или- 1000000(Леорды)(Вороны)- 10000000Славянская кириллическая нумерация
- 15. Пьер Симон Лаплас (1749 – 1827 гг.)«Мысль
- 16. Позиционные системы -системы счисления, в которых
- 17. Десятичная система счисленияЦифры 1234567890 сложились в
- 18. Экскурс в прошлое и настоящее позиционных систем счисленияПятеричнаяДесятеричнаяДвадцатеричнаяДвенадцатеричнаяШестидесятеричнаяДвоичнаяВосьмеричнаяШестнадцатеричная
- 19. Биологические системы счисленияПятеричная система счисленияШироко применялась в
- 20. Таинственная история существования двенадцатеричной системы!Происхождение тоже связано
- 21. Машинные системы счисленияИз данной таблицы видно, что
- 22. Двоичная система счисления1 0
- 23. Общие правила сложения для любых систем
- 24. Правила сложения в любых системах счисленияДействия производят
- 25. Двоичная с/с
- 26. Перевод целой части числа из 10-ой с/с
- 27. Перевод дробной части числа из 10-ой с/с
- 28. Перевод из любой с/с в
- 29. Перевод в машинных с/сВ 8-ую или 16-ую
- 30. ЗадачиМужчине 45 лет, через 5 лет, когда
Слайд 2Давайте обсудим
… Обучение я закончил в 44 года. Через год 100
Прошлое:
Китайский счет (суаньпан)
Настоящее:
Счет на математике в любых системах
Ученые за 12-ричную с.с
Рождение 6-палых детей
Будущее:
Исследования космоса
Совершенствование компьютера
Шведский король Карл XII в 1717 г. увлекся этой системой и собирался ввести ее как общегосударственную
Слайд 5Системы счисления
Общие понятия
Экскурс в прошлое и настоящее позиционных с/с.
Таблица переводов
Правила математики
Правила
Слайд 6Общие понятия
Система счисления -
это алфавит определенных символов, связанных с количественной
правила работы с ним
Классификация
Слайд 8Унарные системы
Число образуется путем повторения
одного знака, символизирующего
единицу.
Примеры:
зарубки
черточки
палочки
10 - 11
Слайд 9Непозиционные системы -
системы счисления, в которых каждой цифре соответствует величина, не
Египетская
Римская
Древнегреческая
Славянская
XXIV
Слайд 14- 1000
- 7000
- 2000
- 10000
- 20000
- 50000
(Тьма)
- 200000
- 100000
(Легионы)
или
- 1000000
(Леорды)
(Вороны)
- 10000000
Славянская
Слайд 15Пьер Симон Лаплас
(1749 – 1827 гг.)
«Мысль – выражать все числа
придавая им значение по форме,
еще значение по месту,
настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна …»
(Вес числа зависит от номера позиции 444 – четыреста сорок четыре 4*102+4*101 +4*100)
Слайд 16Позиционные системы -
системы счисления, в которых вес цифры зависит от
Название системы зависит от количества используемых в ней цифр.
Десятичная 0÷ 9
Двоичная 0 ÷ 1
Восьмеричная 0 ÷7
Двенадцатеричная 0 ÷ 11
и др.
Мнение:
Слайд 17Десятичная
система счисления
Цифры 1234567890
сложились в Индии
около 400 г. н.
Арабы стали пользоваться
подобной нумерацией около 800 г. н. э.
Примерно в 1200 г. н. э. эту
нумерацию начали применять в Европе.
Слайд 18Экскурс в прошлое и настоящее
позиционных систем счисления
Пятеричная
Десятеричная
Двадцатеричная
Двенадцатеричная
Шестидесятеричная
Двоичная
Восьмеричная
Шестнадцатеричная
Слайд 19Биологические системы счисления
Пятеричная система счисления
Широко применялась в Африке и Китае.
Счеты
Десятеричную систему применяют и в век компьютерных технологий, потому что это удобно.
Коза-коза- аракоза
При двадцатеричной системе счисления у ацтеков, майя, кельтов для того чтобы показать число 35 один человек садился вытянув ноги и руки, а другой вытягивал ноги и выставлял кисть с растопыренными пальцами.
Во французской денежной системе основная единица 1 франк = 20 су.
Слайд 20Таинственная история существования двенадцатеричной системы!
Происхождение тоже связано со счетом на пальцах.
Есть исследовательский материал о том, что у предыдущего поколения человечества было не 5, а 6 пальцев на одной руке.
Следы двенадцатеричной системы счисления сохранились в Англии в системе мер (1 фут — 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам). Нередко и мы сталкиваемся в быту с двенадцатеричной системой счисления: чайные и столовые сервизы на 12 персон, комплект носовых платков — 12.
Современные астрофизики считают, что все человечество необходимо перевести на эту систему счисления, так как у числа - 12 множителей больше чем у 10, и более сложные вычисления легче выполнять в этой системе. И лишь психологи и социологи препятствуют этим изменениям!
Слайд 21Машинные системы счисления
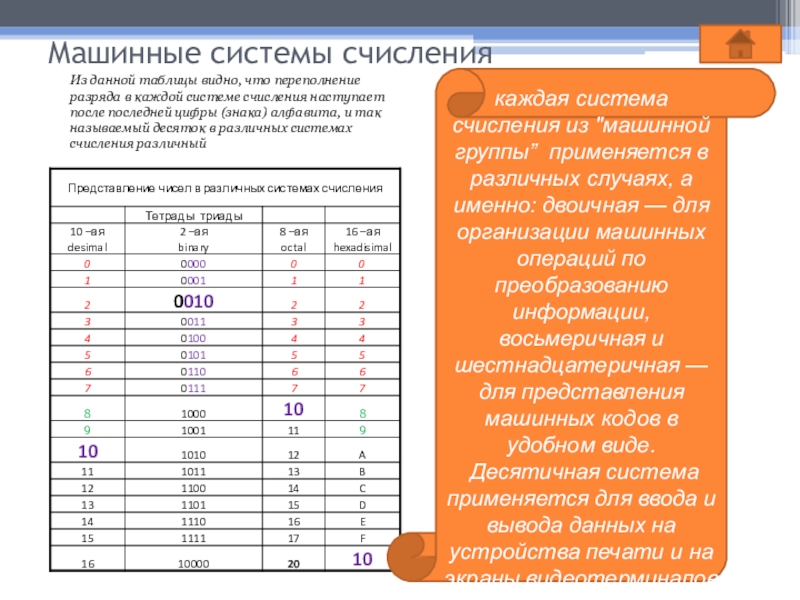
Из данной таблицы видно, что переполнение разряда в каждой
каждая система счисления из "машинной группы” применяется в различных случаях, а именно: двоичная — для организации машинных операций по преобразованию информации, восьмеричная и шестнадцатеричная — для представления машинных кодов в удобном виде.
Десятичная система применяется для ввода и вывода данных на устройства печати и на экраны видеотерминалов
Слайд 22Двоичная система счисления
1 0 1
Используются две цифры – 0 и 1
Применяются в технических устройствах
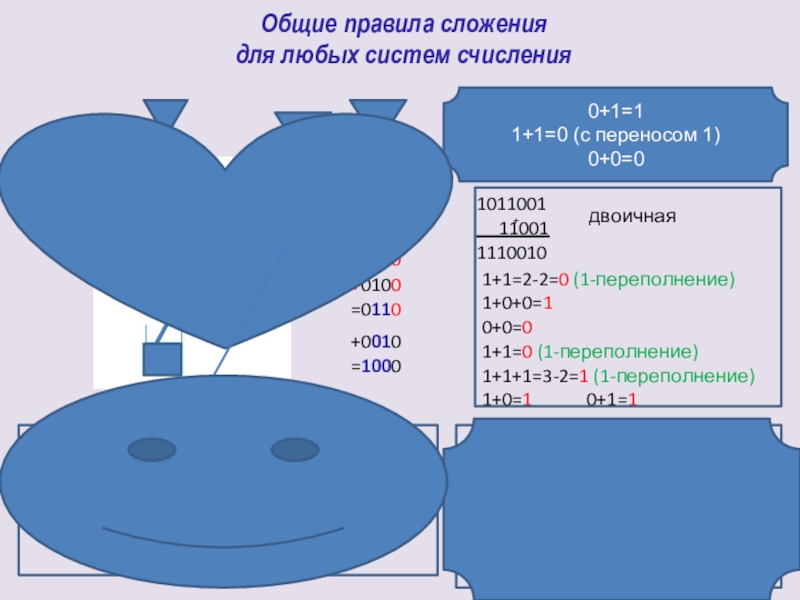
Слайд 23Общие правила сложения
для любых систем счисления
0000
+0001
=0001
+0001
=0010
+0100
=0110
+0010
=1000
25 87
112
десятичная
1011001
1110010
₊
двоичная
25
76
123
₊
восьмеричная
1+1=2-2=0 (1-переполнение)
1+0+0=1
0+0=0
1+1=0 (1-переполнение)
1+1+1=3-2=1 (1-переполнение)
1+0=1 0+1=1
5+6=11-8=3 (1 – переполнение )
2+7+1 = 10-8 =2 (1 – переполнение )
шестнадцатеричная
4A8BC
E5 F23
1307DF
₊
(C)12 +3=15(F)
(B)11+2=13 (D)
(F)15+8=23-16=7(1)
(A)10+5+1=16-16=0(1)
(E)14+4+1=19-16=3(1)
5+7=12-10=2(1)
1+2+8=11-10=1(1)
0+1=1
1+1=0 (с переносом 1)
0+0=0
12
1
Слайд 24Правила сложения в любых системах счисления
Действия производят начиная с правого крайнего
Если сумма больше или равна основанию системы счисления, то из нее вычитают основание
Разность записывают в этот разряд, а 1, означающую переполнение, - в старший разряд
Такие же действия производят со всеми числами во всех разрядах по мере возрастания их нумерации.
Сумма должна быть больше любого слагаемого
Слайд 25Двоичная с/с
1 1 2
1 0 1 1 0
1 0 0 1 1 0 0
Восмеричная с/с
7 7 8
6 3 0 0 2 7 0
1 0 4 2 0
6 2 6 7 6 5 0
Шестнадцатеричная с/с
15 1516
6 3 0 0 B 7 A
8 0 E 2 A
6 2 7 F D 5 0
Вычитание в различных системах счисления
Правила обычные, если уменьшаемое больше вычитаемого.
Иначе занимаем у предыдущего число, равное основанию системы счисления и далее обычный алгоритм
Пример:
-
-
-
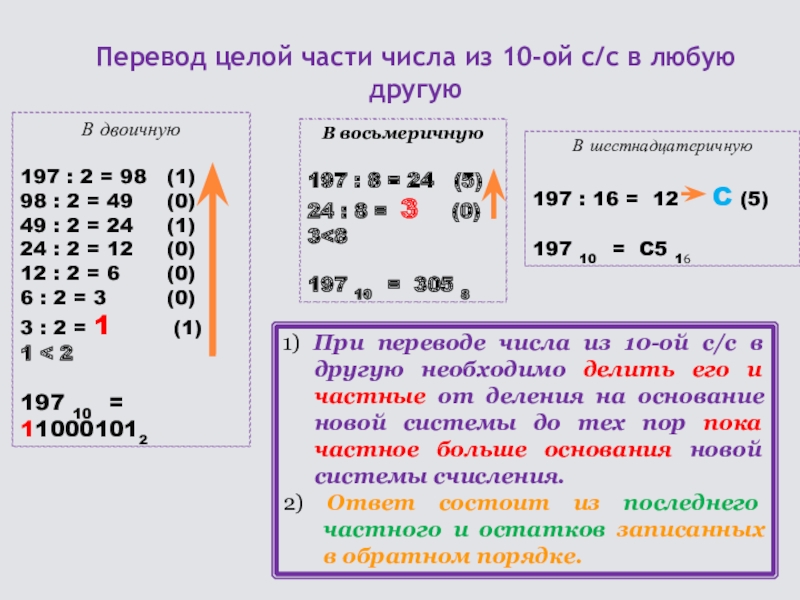
Слайд 26Перевод целой части числа из 10-ой с/с в любую другую
В двоичную
197
98 : 2 = 49 (0)
49 : 2 = 24 (1)
24 : 2 = 12 (0)
12 : 2 = 6 (0)
6 : 2 = 3 (0)
3 : 2 = 1 (1)
1 < 2
197 10 = 110001012
В восьмеричную
197 : 8 = 24 (5)
24 : 8 = 3 (0)
3<8
197 10 = 305 8
В шестнадцатеричную
197 : 16 = 12 C (5)
197 10 = C5 16
1) При переводе числа из 10-ой с/с в другую необходимо делить его и частные от деления на основание новой системы до тех пор пока частное больше основания новой системы счисления.
2) Ответ состоит из последнего частного и остатков записанных в обратном порядке.
Слайд 27Перевод дробной части числа из 10-ой с/с в любую другую
В двоичную
0,
0,7 * 2 = 1, 4
0,4 * 2 = 0,8
0,8 * 2 = 1,6
0,6 * 2 = 1,2
0,2 * 2 = 0,4
0,4 * 2 = 0,8
0,8 * 2 = 1,6
Начинается периодичность
0,85 10 = 0,11(0110)2
В восьмеричную
0,85 * 8 = 6,8
0,8 * 8 = 6,4
0,4 * 8 = 3,2
0,2 * 8 = 1,6
0,6 * 8 = 4,8
0,8 * 8 = 6,4
0,8510 = 0,6(6314)8
В шестнадцатеричную
0,85 *16 =
13,6 D,6
0,6 * 16 = 9,6
0,6 * 16 = 9,6
0,85 10 = 0,D(9)16
Правило
Умножаем только дробные части числа и произведений на основание новой системы счисления, до тех пор пока в дробной части не будут «0» или не появиться периодичность, или до указанной точности.
Ответ не содержит целой части, а дробная состоит из целых частей произведений, записанных в прямом порядке.
Слайд 28Перевод из любой с/с в
Проставить над каждой цифрой номер позиции
(№ позиции самого младшего разряда целой части - 0)
Записать сумму произведений цифры на основание с/с в степени номера позиции.
Выполнить вычисления.
Примеры
Из двоичной :
1011012
≈150413 120110
≈1 · 25 +0· 24 +1 · 23 +1· 22 +0· 21 +1· 20
= 32+0+8+4+0+ 1 = 45 10
Из восьмеричной:
12378
≈13 223170
≈1 · 83 +2· 82 +3· 81 +7· 80
= 512+128+24+ 7 = 671 10
Из шестнадцатеричной:
1A2B16
≈13 A221B0
≈1 · 163 +10· 162 +2· 161 +11· 160
= 4096+2560+32+11 = 6699 10
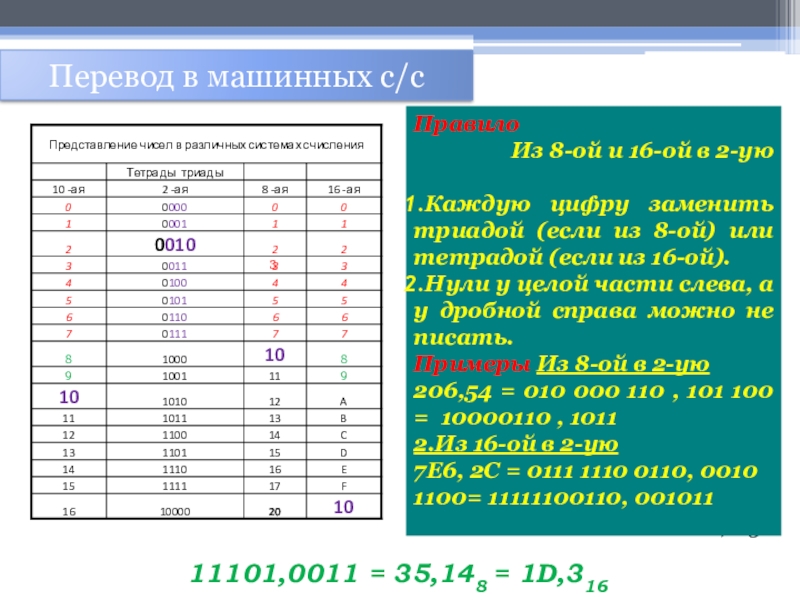
Слайд 29Перевод в машинных с/с
В 8-ую или 16-ую из 2-ой
Разбить число на
Заменить каждую группу из 0 и 1 значением из соответствующего столбца.
Из 2-ой в 8-ую
11101,0011 =
011 101 , 001 100 =
3 5 , 1 4
Из 2-ой в 16-ую
11101,0011 =
0001 1101 , 0011=
1 D , 3
011
3
11101,0011 = 35,148 = 1D,316
Правило
Из 8-ой и 16-ой в 2-ую
Каждую цифру заменить триадой (если из 8-ой) или тетрадой (если из 16-ой).
Нули у целой части слева, а у дробной справа можно не писать.
Примеры Из 8-ой в 2-ую
206,54 = 010 000 110 , 101 100 = 10000110 , 1011
2.Из 16-ой в 2-ую
7E6, 2C = 0111 1110 0110, 0010 1100= 11111100110, 001011
Слайд 30Задачи
Мужчине 45 лет, через 5 лет, когда ему исполнилось 54 года,
202-х летний молодой человек пошел покупать CD-RW в магазин, который располагался недалеко за углом в 120 минутах ходьбы лт дома. Скорость его была равна 12 км/час. Придя в магазин и выбрав диск, он обнаружил, что в кошельке у него было 1112 р., а еще 11 р., необходимых для покупки диска ценой 1200 р., остались дома в кармане других брюк. За какое время он прошел бы это же расстояние до магазина со скоростью 10 км/час?