- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Представление чисел (10 класс)
Содержание
- 1. Презентация по информатике на тему Представление чисел (10 класс)
- 2. Целые числа в памяти ЭВМВ компьютерной технике
- 3. Положительные числа в прямом, обратном и дополнительном
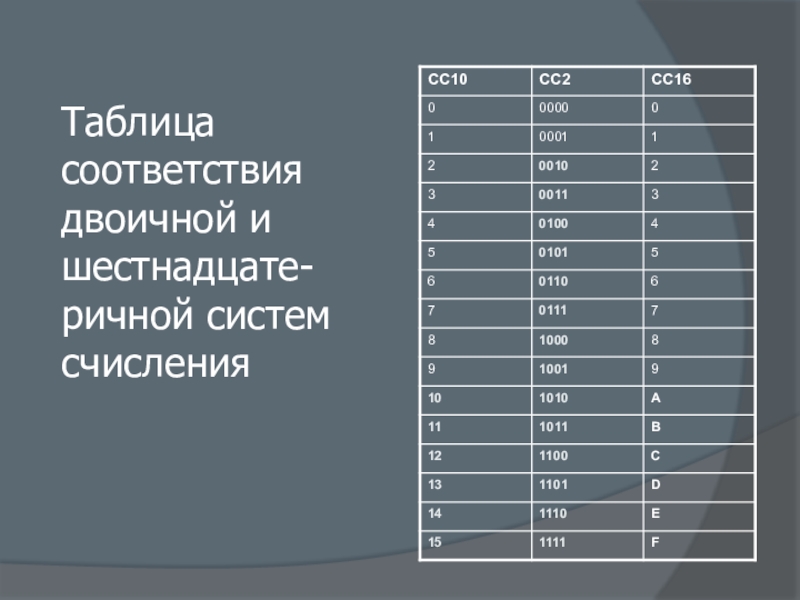
- 4. Таблица соответствия двоичной и шестнадцате-ричной систем счисления
- 5. Представление целых чиселПоложительные числаПеревести число в двоичную
- 6. Самостоятельная работаВыписать внутреннее представление чисел: 1) 264-195
- 7. Домашнее задание1)Выписать внутреннее представление чисел 234 и
- 8. Представление вещественных чисел в памяти компьютера
- 9. В компьютере используется нормализированное представление числа в форме с плавающей точкой 0,1≤М
- 10. Для записи внутреннего представления вещественного числа необходимо:Перевести
- 11. ВОПРОСЫ ТЕСТОВ Как представлено число 2510
- 12. ВОПРОСЫ ТЕСТОВ Двоичное изображение десятичного числа
- 13. Контрольная работа
Слайд 2Целые числа в памяти ЭВМ
В компьютерной технике применяются три формы записи
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.
Слайд 3Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково —
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины.
Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями.
Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
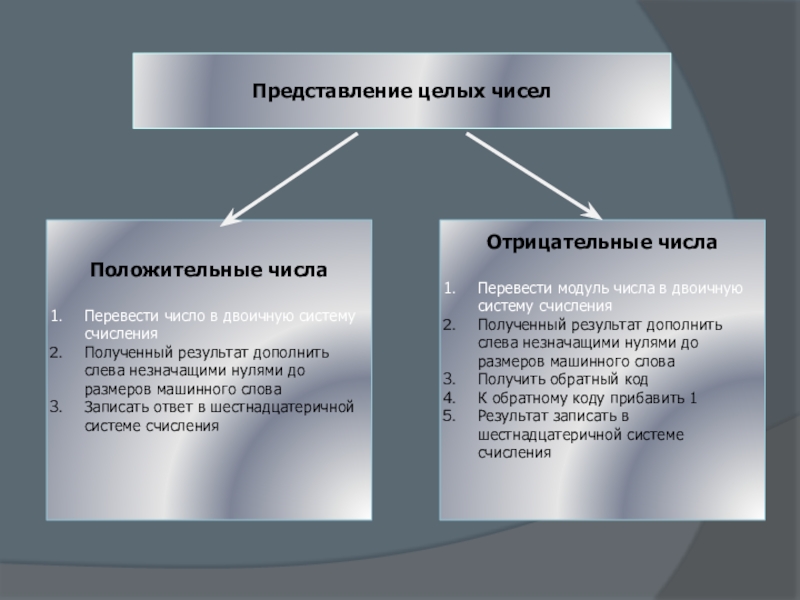
Слайд 5Представление целых чисел
Положительные числа
Перевести число в двоичную систему счисления
Полученный результат дополнить
Записать ответ в шестнадцатеричной системе счисления
Отрицательные числа
Перевести модуль числа в двоичную систему счисления
Полученный результат дополнить слева незначащими нулями до размеров машинного слова
Получить обратный код
К обратному коду прибавить 1
Результат записать в шестнадцатеричной системе счисления
Слайд 7Домашнее задание
1)Выписать внутреннее представление чисел 234 и -145
2) Сколько единиц в
3) Вычислите значение выражения 1016 + 108 · 102 в двоичной системе счисления.
4)Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Повторить:
перевод чисел из десятичной системы в двоичную
перевод чисел из двоичной системы в десятичную
двоичную арифметику
Слайд 8Представление вещественных чисел в памяти компьютера
Любое число N
N = M * qp , где M называется мантиссой числа, а p — порядком. Такой способ записи чисел называется представлением с плавающей точкой.
Если “плавающая” точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует:
Мантисса должна быть правильной дробью, первая цифра которой отлична от нуля:
M из [0.1, 1).
Такое, наиболее выгодное для компьютера, представление вещественных чисел называется нормализованным.
Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q,
а само основание — в десятичной системе.
Примеры нормализованного представления:
Десятичная система Двоичная система
753.15 = 0.75315*103; -101.01 = -0.10101*211 (порядок 112 = 310)
-0.000034 = -0.34*10-4; -0.000011 = 0.11*2-100 (порядок -1002 = -410)
Слайд 9В компьютере используется нормализированное представление числа в форме с плавающей точкой
В памяти ЭВМ мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранится). Следовательно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.
Машинный порядок смещен относительно математического и имеет только положительные значения.
Связь между машинным порядком и математическим выражается формулой: Мр=р+64;
Мр2=р2+10000002
В 4-х байтовой ячейки памяти:
{ 1 байт } { 2 байт} { 3байт} { 4 байт}
8 + 24
Слайд 10Для записи внутреннего представления вещественного числа необходимо:
Перевести модуль числа в СС2
Нормализовать двоичное число.
Найти машинный порядок в СС2.
Учитывая знак числа, выписать его представление в 4-х байтовом машинном слове.
ПРИМЕРЫ:
1. Определить внутреннее представление числа 250,1875.
2. По 16-ой форме внутреннего представления числа в форме с «плавающей точкой» С9811000 восстановить число.
Слайд 11ВОПРОСЫ ТЕСТОВ
Как представлено число 2510 в двоичной системе счисления?
А)
В) 100112; Г) 110102.
Вычислите значение суммы 102 + 108 +1016 в двоичной системе счисления.
А) 10100010; Б) 11110;
В) 11010; Г) 10100.
Как представлено число 831О в двоичной системе счисления?
А) 10010112; Б) 11001012;
В) 10100112; Г) 1010012.
Вычислите сумму двоичных чисел х и у, если х = 10101012 , у = 10100112
А) 101000102; Б) 101010002;
В)101001002; Г) 101110002.
Восьмеричная система счисления отличается от двоичной:
А) количеством цифр, используемых для записи чисел;
Б) количеством требуемой памяти компьютера;
В) скоростью обращения к данным;
Г) возможностью кодировать символы.
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Слайд 12ВОПРОСЫ ТЕСТОВ
Двоичное изображение десятичного числа 1025 содержит значащих нулей:
А)
В) 11; Г) 9.
В двоичной системе сумма 112 + 118 + 1116 равна:
А) 11001; Б) 11100;
В) 11001; Г) 11101.
Если буквы A, B, C, D, Е имеют, соответственно, коды 10, 11, 111, 000, 1000, то двоичной последовательностью вида 1011111000111000 не может быть закодирована лишь строка:
А) ABCDCD; Б) АCBDCD;
В) ABCDBE; Г) ABCDBD.
Если текст АРБА закодирован как 0011110001, причем гласные и согласные закодированы различным количеством битов, то закрытому сообщению 1000111 по этому коду соответствует открытое сообщение:
А) БАР; Б) РАБ;
В) РАБА; Г) АББА.
Вычислите сумму чисел x и y, при x = 1D16, y = 728. Результат представьте в двоичной системе счисления.
А)100011112 Б)11001012
В)1010112 Г)10101112
Если в некоторой системе счисления десятичное число 47 записывается в виде 52, то чему равно основание этой системы?