о способах рассуждений и доказательств.
Объектами логики являются высказывания.
Высказывание – это любое предложение какого-либо языка (утверждение), содержание которого можно определить как истинное или ложное.
Всякое высказывание или истинно, или ложно; быть одновременно и тем и другим оно не может!!!
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Основы алгебры логики
Содержание
- 1. Презентация по информатике на тему Основы алгебры логики
- 2. ВысказыванияпростыесоставныеА = «Два умножить на два равно
- 3. Основные операции алгебры высказыванийЛогическое умножение (конъюнкция).Объединение двух
- 4. Таблица истинности конъюнкции.«2 ⋅2 = 5 и
- 5. 2. Логическое сложение (дизъюнкция).Объединение двух (или нескольких)
- 6. Таблица истинности дизъюнкции.«2 ⋅2 = 5 и
- 7. Логическое отрицание (инверсия).Присоединение частицы «не» к высказыванию
- 8. Таблица истинности инверсии.Пусть А = «Два умножить
- 9. Логическое выражение – это формула, в которую
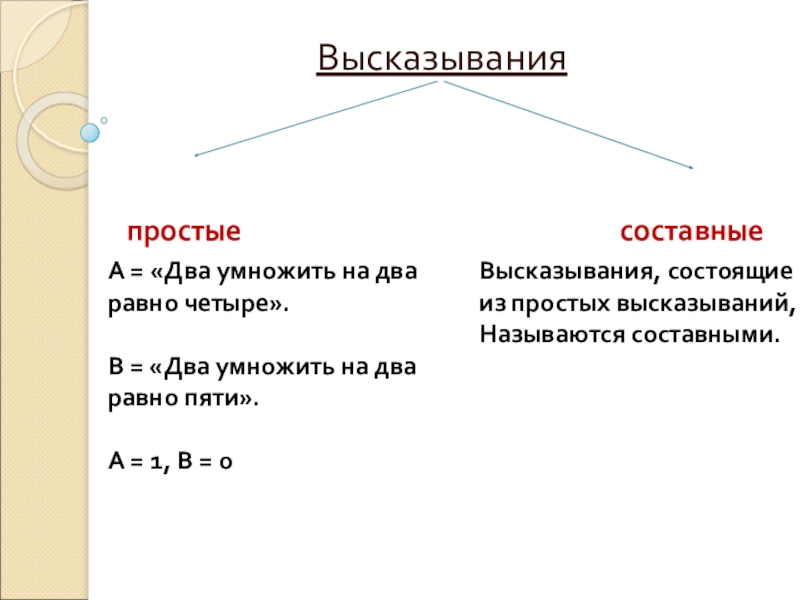
ВысказыванияпростыесоставныеА = «Два умножить на два равно четыре».В = «Два умножить на два равно пяти».А = 1, В = 0Высказывания, состоящие из простых высказываний,Называются составными.
Слайд 2Высказывания
простые
составные
А = «Два умножить на два равно четыре».
В = «Два умножить
на два равно пяти».
А = 1, В = 0
А = 1, В = 0
Высказывания, состоящие
из простых высказываний,
Называются составными.
Слайд 3Основные операции алгебры высказываний
Логическое умножение (конъюнкция).
Объединение двух (или нескольких) высказываний в
одно с помощью союза «и» называется конъюнкцией.
Составное высказывание, образованное в результате операции конъюнкции, истинно, если истинны все входящие в него простые высказывания.
Составное высказывание, образованное в результате операции конъюнкции, истинно, если истинны все входящие в него простые высказывания.
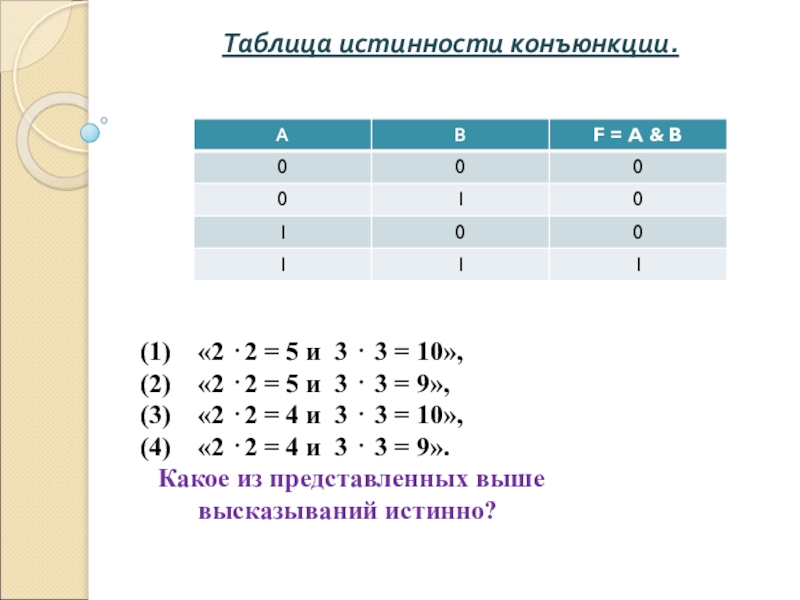
Слайд 4Таблица истинности конъюнкции.
«2 ⋅2 = 5 и 3 ⋅ 3 =
10»,
«2 ⋅2 = 5 и 3 ⋅ 3 = 9»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 10»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 9».
Какое из представленных выше высказываний истинно?
«2 ⋅2 = 5 и 3 ⋅ 3 = 9»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 10»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 9».
Какое из представленных выше высказываний истинно?
Слайд 52. Логическое сложение (дизъюнкция).
Объединение двух (или нескольких) высказываний в одно с
помощью союза «или» называется дизъюнкцией.
Составное высказывание, образованное в результате операции дизъюнкции, истинно, если истинно хотя бы одно из входящих в него простых высказываний.
Составное высказывание, образованное в результате операции дизъюнкции, истинно, если истинно хотя бы одно из входящих в него простых высказываний.
Слайд 6Таблица истинности дизъюнкции.
«2 ⋅2 = 5 и 3 ⋅ 3 =
10»,
«2 ⋅2 = 5 и 3 ⋅ 3 = 9»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 10»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 9».
Какие из представленных выше высказываний истинны?
«2 ⋅2 = 5 и 3 ⋅ 3 = 9»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 10»,
«2 ⋅2 = 4 и 3 ⋅ 3 = 9».
Какие из представленных выше высказываний истинны?
Слайд 7Логическое отрицание (инверсия).
Присоединение частицы «не» к высказыванию называется операцией логического отрицания
или инверсией.
Логическое отрицание или инверсия делает истинное высказывание ложным и, наоборот, ложное – истинным.
Логическое отрицание или инверсия делает истинное высказывание ложным и, наоборот, ложное – истинным.
Слайд 8Таблица истинности инверсии.
Пусть А = «Два умножить на два равно четырем»
-
истинное высказывание. Тогда высказывание F = «Два
умножить на два НЕ равно четырем», образованное
с помощью операции логического отрицания, - ложно.
истинное высказывание. Тогда высказывание F = «Два
умножить на два НЕ равно четырем», образованное
с помощью операции логического отрицания, - ложно.
Слайд 9Логическое выражение – это формула, в которую входят логические переменные (высказывания),
и знаки логических операций (логические функции).
Запишем в форме логического выражения составное высказывание, содержащее 2 простых высказывания:
«(2 ⋅ 2 = 5 или 2 ⋅ 2 = 4) и (2 ⋅ 2 ≠ 5 или 2 ⋅ 2 ≠ 4)»
Запишем в форме логического выражения составное высказывание, содержащее 2 простых высказывания:
«(2 ⋅ 2 = 5 или 2 ⋅ 2 = 4) и (2 ⋅ 2 ≠ 5 или 2 ⋅ 2 ≠ 4)»