- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Моделирование в Excel
Содержание
- 1. Презентация по информатике на тему Моделирование в Excel
- 2. «СРЕДА»MS Excel – разновидность электронной таблицы. Это программа
- 3. Рассмотрим задачу исследования физических моделей. Построим информационную модель движения тела, брошенного под углом к горизонту
- 4. 1 этапСодержательная постановка задачи «Бросание мячика в площадку». В
- 5. Проведём формализацию задачиФормулируем основные предположения:· мячик мал по
- 6. Выводможно использовать формулы для равноускоренного движения, известные из курса физики.
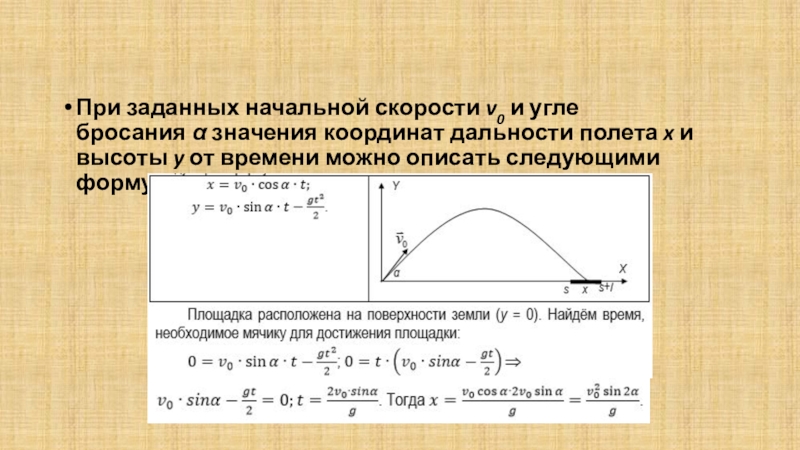
- 7. При заданных начальной скорости v0 и угле бросания α значения координат дальности полета x и высоты y от времени можно описать следующими формулами:
- 8. 2 этапПостроение компьютерной модели движения тела в среде MS Excel.
- 9. Слайд 9
- 10. 3 этапИсследование моделиИсследуем модель и определим с
- 11. Слайд 11
- 12. Для определения диапазона углов используем метод Подбор параметра. Этот
- 13. Слайд 13
- 14. Далее, найдем угол бросания, который обеспечит попадание
- 15. Итак, существует диапазон значений угла бросания мячика
- 16. 4 этапАнализ результатов моделирования и принятие решения. Данная
«СРЕДА»MS Excel – разновидность электронной таблицы. Это программа обработки числовых данных, хранящая и обрабатывающая данные в прямоугольных таблицах.Таким образом, с помощью этой программы можно решать задачи исследовательского характера, требующие большого количества вычислений.
Слайд 2«СРЕДА»
MS Excel – разновидность электронной таблицы. Это программа обработки числовых данных, хранящая
и обрабатывающая данные в прямоугольных таблицах.
Таким образом, с помощью этой программы можно решать задачи исследовательского характера, требующие большого количества вычислений.
Таким образом, с помощью этой программы можно решать задачи исследовательского характера, требующие большого количества вычислений.
Слайд 3Рассмотрим задачу исследования физических моделей. Построим информационную модель движения тела, брошенного под углом к горизонту
Слайд 41 этап
Содержательная постановка задачи «Бросание мячика в площадку». В процессе тренировок теннисистов используются
автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии.
Слайд 5Проведём формализацию задачи
Формулируем основные предположения:
· мячик мал по сравнению с Землей, поэтому
его можно считать материальной точкой;
· изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с2 и движение по оси 0Y можно считать равноускоренным;
· скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОX можно считать равномерным.
· изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с2 и движение по оси 0Y можно считать равноускоренным;
· скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОX можно считать равномерным.
Слайд 7При заданных начальной скорости v0 и угле бросания α значения координат дальности полета x и высоты y от времени
можно описать следующими формулами:
Слайд 103 этап
Исследование модели
Исследуем модель и определим с заданной точностью 0,1 градуса
значения диапазона углов бросания, которые обеспечивают попадание мячика в мишень (например, при скорости бросания v0 = 18 м/с в площадку длиной l = 1 м, находящуюся на расстоянии S = 30 м).
Слайд 12Для определения диапазона углов используем метод Подбор параметра. Этот метод позволяет задать значение
функции и найти значение аргумента функции, который обеспечивает требуемое значение функции.
Функцией в нашем случае будет являться зависимость координаты тела x от параметра, т.е. угла бросания α. Для определения диапазона углов, необходимо определить два угла, которые обеспечивают попадания в ближний и дальний края площадки. Для заданных начальных условий (скорости бросания и расстояния до мишени) проведем поиск углов, которые дают попадание в площадку на расстояниях S = 30 м и S + l = 31 м.
Ищем значение угла бросания, которое обеспечит попадание мячика в ближний край площадки, т.е. какой угол α обеспечивает значение функции x = 30 метров.
Функцией в нашем случае будет являться зависимость координаты тела x от параметра, т.е. угла бросания α. Для определения диапазона углов, необходимо определить два угла, которые обеспечивают попадания в ближний и дальний края площадки. Для заданных начальных условий (скорости бросания и расстояния до мишени) проведем поиск углов, которые дают попадание в площадку на расстояниях S = 30 м и S + l = 31 м.
Ищем значение угла бросания, которое обеспечит попадание мячика в ближний край площадки, т.е. какой угол α обеспечивает значение функции x = 30 метров.
Слайд 14Далее, найдем угол бросания, который обеспечит попадание мячика в дальний край
площадки, т.е. какой угол α обеспечивает значение функции x = 30 м + 1 м = 31 м.
Слайд 15Итак, существует диапазон значений угла бросания мячика от 32,6° до 34,9°, в
котором обеспечивается попадание в площадку длиной 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.
Можно повторить исследование модели при другом начальном значении угла (например, 55°).
Можно повторить исследование модели при другом начальном значении угла (например, 55°).
Слайд 164 этап
Анализ результатов моделирования и принятие решения. Данная компьютерная модель позволяет решить
поставленную задачу по исследованию движения тела, брошенного под углом к горизонту, подобрать оптимальные значения начальной скорости и угла бросания.