Презентация, доклад по информатике на тему Кодирование и декодирование информации. Подготовка к ЕГЭ (11 класс)

Содержание

1. Презентация по информатике на тему Кодирование и декодирование информации. Подготовка к ЕГЭ (11 класс)
2. 1) Для кодирования букв О, В, Д,
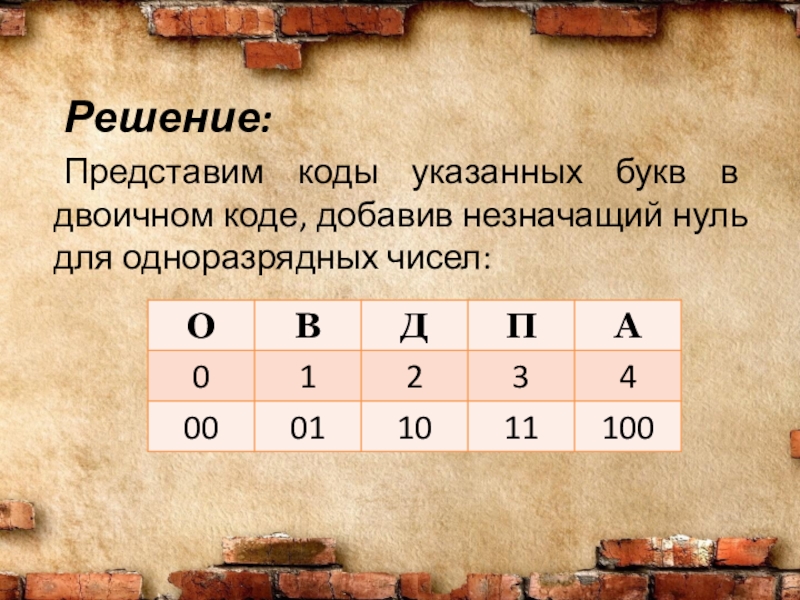
3. Решение: Представим коды указанных букв в двоичном коде, добавив незначащий нуль для одноразрядных чисел:
4. Закодируем последовательность букв:ВОДОПАД – 010010001110010. Разобьем это
5. Решите самостоятельно: 2) Для передачи по каналу связи
6. 3) Для 5 букв латинского алфавита заданы
7. Решение: Условие Фано и обратное условие Фано не
8. Решение: Первая буква определяется однозначно, ее код 100:
9. 4) Для передачи по каналу связи сообщения,
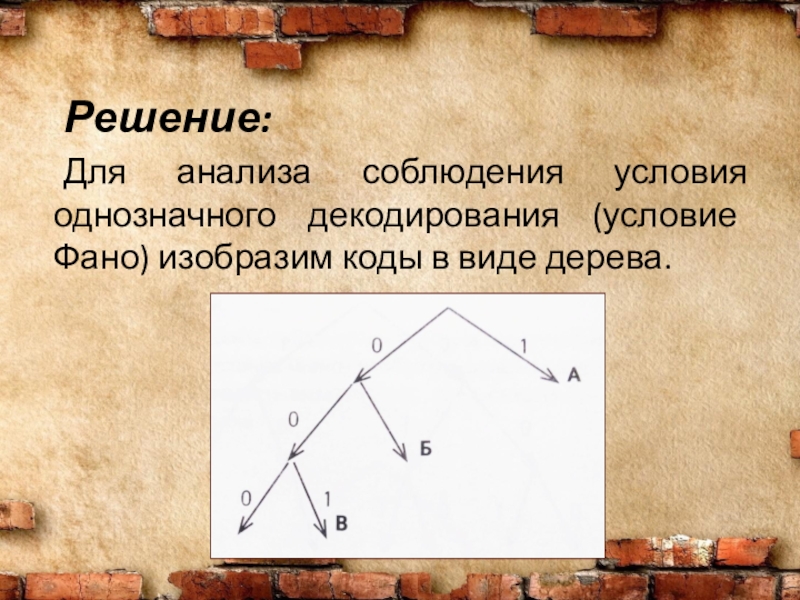
10. Решение: Для анализа соблюдения условия однозначного декодирования (условие Фано) изобразим коды в виде дерева.
11. Решение: Тогда однозначность выполняется, если каждая буква является
12. Решите самостоятельно: 5) Для кодирования некоторой последовательности, состоящей
13. Выберите правильный вариант ответа: 1) кодовое слово для
14. 6) Для кодирования некоторой последовательности, состоящей из
15. Решение: Условие Фано означает, что никакое кодовое слово
16. Решение: Легко заметить, что ближайшие от корня свободные
17. Решите самостоятельно: 7) По каналу связи передаются сообщения,
18. Ответы:Задача 2): D3A616 Задача 5): кодовое слово для буквы Н можно сократить до 10.
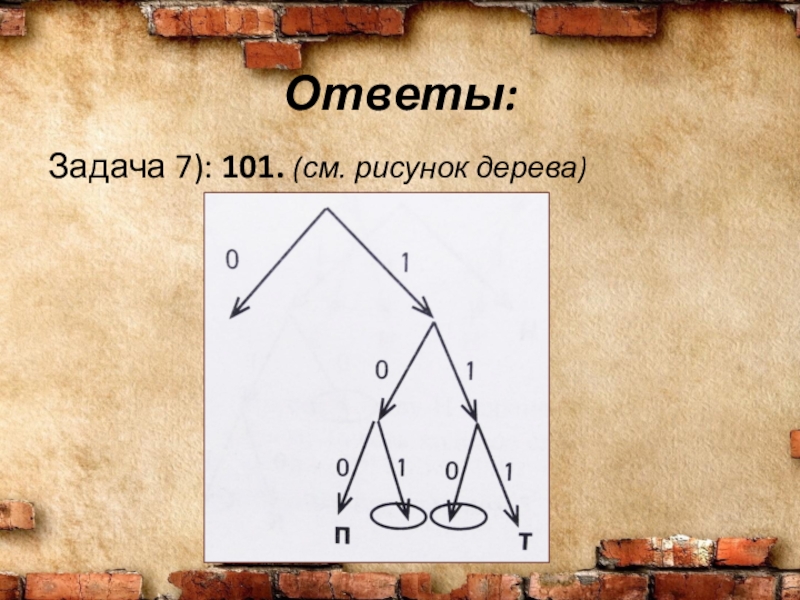
19. Ответы:Задача 7): 101. (см. рисунок дерева)

1) Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления. Если закодировать последовательность букв ВОДОПАД таким

Главная
Информатика
Презентация по информатике на тему Кодирование и декодирование информации. Подготовка к ЕГЭ (11 класс)

Слайд 1КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ИНФОРМАЦИИ (Подготовка к ЕГЭ)
Гаджиево, 2019

Слайд 2 1) Для кодирования букв О, В, Д, П, А решили использовать

двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления. Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится:
22162 3) 2131453
1020342 4) 34017

1) Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2,

Слайд 3 Решение:
Представим коды указанных букв в двоичном коде, добавив незначащий нуль для

одноразрядных чисел:

Слайд 4

Закодируем последовательность букв:
ВОДОПАД – 010010001110010.
Разобьем это представление на тройки

справа налево и переведем каждую тройку в восьмеричное число.
0100100011100102 = 221628

Закодируем последовательность букв:ВОДОПАД – 010010001110010. Разобьем это представление на тройки справа налево и переведем каждую тройку в

Слайд 5 Решите самостоятельно:
2) Для передачи по каналу связи сообщения, состоящего только из

символов А, Б, В и Г, используется посимвольное кодирование: А – 10, Б – 11, В – 110, Г – 0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный вид.
D3A6 3) 6A3D
62032206 4) CADBAADC

Решите самостоятельно: 2) Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г,

Слайд 6 3) Для 5 букв латинского алфавита заданы их двоичные коды. Эти

коды представлены в таблице:

Определите, какой набор букв закодирован двоичной строкой 1000110110110, если известно, что все буквы в последовательности – разные:
1) cbade 3) acbed
2) acdeb 4) bacde

3) Для 5 букв латинского алфавита заданы их двоичные коды. Эти коды представлены в таблице: Определите, какой набор

Слайд 7 Решение:
Условие Фано и обратное условие Фано не выполняются, значит, код можно

раскодировать неоднозначно.
Следовательно, будем перебирать варианты, пока не получим подходящее слово:
100 011 01 10 110.

Решение: Условие Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно. Следовательно, будем перебирать варианты, пока

Слайд 8 Решение:
Первая буква определяется однозначно, ее код 100: a. Пусть вторая буква

– с, тогда следующая буква – d, потом e и b. Такой вариант удовлетворяет условию, значит, окончательно получили ответ: acdeb.

Решение: Первая буква определяется однозначно, ее код 100: a. Пусть вторая буква – с, тогда следующая буква –

Слайд 9 4) Для передачи по каналу связи сообщения, состоящего только из букв

А, Б, В, Г, решили использовать неравномерный по длине код: А=1, Б=01, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
0001 3) 11
000 4) 101

4) Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать

Слайд 10 Решение:
Для анализа соблюдения условия однозначного декодирования (условие Фано) изобразим коды в

виде дерева.

Слайд 11 Решение:
Тогда однозначность выполняется, если каждая буква является листом дерева.
Видим, что ближайший

от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.

Решение: Тогда однозначность выполняется, если каждая буква является листом дерева. Видим, что ближайший от корня дерева свободный лист (т.е.

Слайд 12 Решите самостоятельно:
5) Для кодирования некоторой последовательности, состоящей из букв У, Ч,

Е, Н, И, К, используется неравномерный двоичный префиксный код: У – 000, Ч – 001, Е – 010, Н – 100, И – 011, К – 11. Можно ли сократить для одной из букв длину кодового слова так, чтобы код остался префиксным? Коды остальных букв меняться не должны.

Решите самостоятельно: 5) Для кодирования некоторой последовательности, состоящей из букв У, Ч, Е, Н, И, К, используется неравномерный

Слайд 13 Выберите правильный вариант ответа:
1) кодовое слово для буквы Е можно сократить

до 01;
2) кодовое слово для буквы К можно сократить до 1;
3) кодовое слово для буквы Н можно сократить до 10;
4) это невозможно.

Префиксный код – это код, в котором ни одно кодовое слово не является началом другого; такие коды позволяют однозначно декодировать полученную двоичную последовательность.

Выберите правильный вариант ответа: 1) кодовое слово для буквы Е можно сократить до 01; 2) кодовое слово для буквы

Слайд 14 6) Для кодирования некоторой последовательности, состоящей из букв К, Л, М,

Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н – 0, для К – 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
7 3) 9
8 4) 10

6) Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, решили использовать неравномерный двоичный код,

Слайд 15 Решение:
Условие Фано означает, что никакое кодовое слово не является началом другого

кодового слова.
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева.

Решение: Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Для анализа соблюдения условия однозначного

Слайд 16 Решение:
Легко заметить,
что ближайшие от
корня свободные
листы – это 10

или 111. Таким образом, наименьшая возможная суммарная длина всех четырёх кодовых слов будет: 1 + 3 + 2 + 3 = 9.

Решение: Легко заметить, что ближайшие от корня свободные листы – это 10 или 111. Таким образом, наименьшая возможная

Слайд 17 Решите самостоятельно:
7) По каналу связи передаются сообщения, содержащие только четыре буквы:

П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т – 111, О – 0, П – 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решите самостоятельно: 7) По каналу связи передаются сообщения, содержащие только четыре буквы: П, О, С, Т; для передачи

Слайд 18Ответы:
Задача 2): D3A616
Задача 5): кодовое слово для буквы Н можно

сократить до 10.

Слайд 19Ответы:
Задача 7): 101. (см. рисунок дерева)

Скачать презентацию

Презентация, доклад по информатике на тему Кодирование и декодирование информации. Подготовка к ЕГЭ (11 класс)

Содержание

Слайд 1КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ИНФОРМАЦИИ (Подготовка к ЕГЭ)
Гаджиево, 2019

Слайд 2 1) Для кодирования букв О, В, Д, П, А решили использовать

Слайд 3 Решение:
Представим коды указанных букв в двоичном коде, добавив незначащий нуль для

Слайд 4

Закодируем последовательность букв:
ВОДОПАД – 010010001110010.
Разобьем это представление на тройки

Слайд 5 Решите самостоятельно:
2) Для передачи по каналу связи сообщения, состоящего только из

Слайд 6 3) Для 5 букв латинского алфавита заданы их двоичные коды. Эти

Слайд 7 Решение:
Условие Фано и обратное условие Фано не выполняются, значит, код можно

Слайд 8 Решение:
Первая буква определяется однозначно, ее код 100: a. Пусть вторая буква

Слайд 9 4) Для передачи по каналу связи сообщения, состоящего только из букв

Слайд 10 Решение:
Для анализа соблюдения условия однозначного декодирования (условие Фано) изобразим коды в

Слайд 11 Решение:
Тогда однозначность выполняется, если каждая буква является листом дерева.
Видим, что ближайший

Слайд 12 Решите самостоятельно:
5) Для кодирования некоторой последовательности, состоящей из букв У, Ч,

Слайд 13 Выберите правильный вариант ответа:
1) кодовое слово для буквы Е можно сократить

Слайд 14 6) Для кодирования некоторой последовательности, состоящей из букв К, Л, М,

Слайд 15 Решение:
Условие Фано означает, что никакое кодовое слово не является началом другого

Слайд 16 Решение:
Легко заметить,
что ближайшие от
корня свободные
листы – это 10

Слайд 17 Решите самостоятельно:
7) По каналу связи передаются сообщения, содержащие только четыре буквы:

Слайд 18Ответы:
Задача 2): D3A616
Задача 5): кодовое слово для буквы Н можно

Слайд 19Ответы:
Задача 7): 101. (см. рисунок дерева)

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по информатике на тему Кодирование и декодирование информации. Подготовка к ЕГЭ (11 класс)

Содержание

Слайд 1КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ИНФОРМАЦИИ (Подготовка к ЕГЭ)Гаджиево, 2019

Слайд 2 1) Для кодирования букв О, В, Д, П, А решили использовать

Слайд 3 Решение: Представим коды указанных букв в двоичном коде, добавив незначащий нуль для

Слайд 4 Закодируем последовательность букв:ВОДОПАД – 010010001110010. Разобьем это представление на тройки

Слайд 5 Решите самостоятельно: 2) Для передачи по каналу связи сообщения, состоящего только из

Слайд 6 3) Для 5 букв латинского алфавита заданы их двоичные коды. Эти

Слайд 7 Решение: Условие Фано и обратное условие Фано не выполняются, значит, код можно

Слайд 8 Решение: Первая буква определяется однозначно, ее код 100: a. Пусть вторая буква

Слайд 9 4) Для передачи по каналу связи сообщения, состоящего только из букв

Слайд 10 Решение: Для анализа соблюдения условия однозначного декодирования (условие Фано) изобразим коды в

Слайд 11 Решение: Тогда однозначность выполняется, если каждая буква является листом дерева. Видим, что ближайший

Слайд 12 Решите самостоятельно: 5) Для кодирования некоторой последовательности, состоящей из букв У, Ч,

Слайд 13 Выберите правильный вариант ответа: 1) кодовое слово для буквы Е можно сократить

Слайд 14 6) Для кодирования некоторой последовательности, состоящей из букв К, Л, М,

Слайд 15 Решение: Условие Фано означает, что никакое кодовое слово не является началом другого

Слайд 16 Решение: Легко заметить, что ближайшие от корня свободные листы – это 10

Слайд 17 Решите самостоятельно: 7) По каналу связи передаются сообщения, содержащие только четыре буквы:

Слайд 18Ответы:Задача 2): D3A616 Задача 5): кодовое слово для буквы Н можно

Слайд 19Ответы:Задача 7): 101. (см. рисунок дерева)

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ИНФОРМАЦИИ (Подготовка к ЕГЭ)
Гаджиево, 2019

Слайд 3 Решение:
Представим коды указанных букв в двоичном коде, добавив незначащий нуль для

Слайд 4

Закодируем последовательность букв:
ВОДОПАД – 010010001110010.
Разобьем это представление на тройки

Слайд 5 Решите самостоятельно:
2) Для передачи по каналу связи сообщения, состоящего только из

Слайд 7 Решение:
Условие Фано и обратное условие Фано не выполняются, значит, код можно

Слайд 8 Решение:
Первая буква определяется однозначно, ее код 100: a. Пусть вторая буква

Слайд 10 Решение:
Для анализа соблюдения условия однозначного декодирования (условие Фано) изобразим коды в

Слайд 11 Решение:
Тогда однозначность выполняется, если каждая буква является листом дерева.
Видим, что ближайший

Слайд 12 Решите самостоятельно:
5) Для кодирования некоторой последовательности, состоящей из букв У, Ч,

Слайд 13 Выберите правильный вариант ответа:
1) кодовое слово для буквы Е можно сократить

Слайд 15 Решение:
Условие Фано означает, что никакое кодовое слово не является началом другого

Слайд 16 Решение:
Легко заметить,
что ближайшие от
корня свободные
листы – это 10

Слайд 17 Решите самостоятельно:
7) По каналу связи передаются сообщения, содержащие только четыре буквы:

Слайд 18Ответы:
Задача 2): D3A616
Задача 5): кодовое слово для буквы Н можно

Слайд 19Ответы:
Задача 7): 101. (см. рисунок дерева)