- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Измерение информации. Содержательный подход. (10 класс)
Содержание
- 1. Презентация по информатике на тему Измерение информации. Содержательный подход. (10 класс)
- 2. Алфавитмножество используемых символов в языкеНапример: А, Б,
- 3. ПовторениеФормула определения информационного веса символа:2i=MИнформационный объем текста:I=K*i
- 4. Задача на повторение: Сообщение, записанное буквами из
- 5. Принцип: Чем больше первоначальная неопределенность знания, тем
- 6. Неопределенность знания о результате некоторого события (бросания
- 7. Узнав результат бросания монеты, вы получили 1 бит информации.Бросание монеты- 0- 1
- 8. Студент на экзамене может получить 2, 3,
- 9. Нужно задать наименьшее количество вопросов, ответами на
- 10. Оценка выше тройки? Да. Остались 4 и
- 11. Друг едет в одном из 8 вагонов
- 12. Главная формула информатики:
- 13. Количество информации i, содержащееся в сообщении об
- 14. В кинотеатре 256 мест. Какое количество информации несет сообщение о номере вашего кресла?2i=256=28Получаем: i=8Пример
- 15. i=log2N (логарифм от N по основанию 2)Здесь
- 16. Если значение N не равно целой
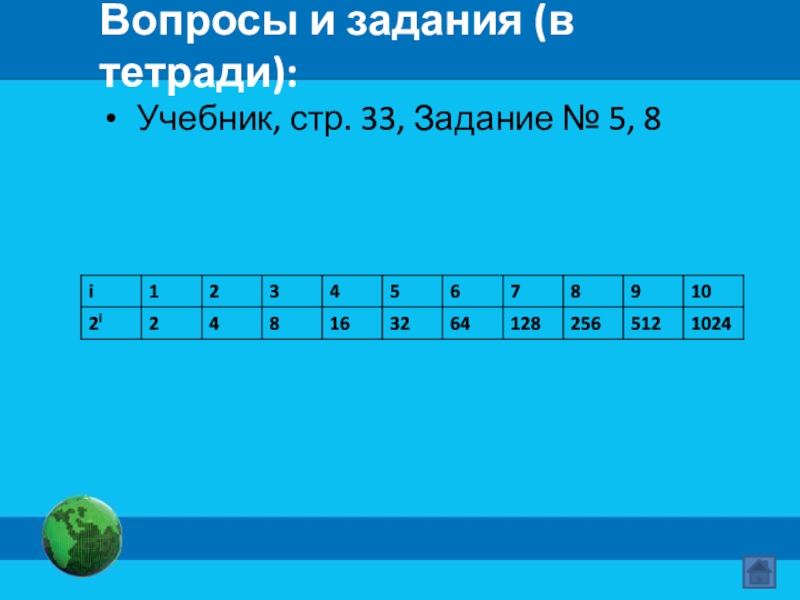
- 17. Вопросы и задания (в тетради): Учебник, стр. 33, Задание № 5, 8
- 18. Домашнее задание: Информатика 10 класс § 4. Измерение информации Содержательный подход
- 19. После окончания работы нужно закрыть все активные программы. Рабочее место нужно оставить чистым.Не забывайте!!!
Алфавитмножество используемых символов в языкеНапример: А, Б, В, . . . ЯМощность алфавита (N) количество символов, используемых в алфавитеНапример: 33Информационный вес символа (i)длина двоичного кода, с помощью которого кодируется символ алфавитаНапример: 100101 - 6 битовПовторение Что такое:
Слайд 2Алфавит
множество используемых символов в языке
Например: А, Б, В, . . .
Я
Мощность алфавита (N)
количество символов, используемых в алфавите
Например: 33
Информационный вес символа (i)
длина двоичного кода, с помощью которого кодируется символ алфавита
Например: 100101 - 6 битов
Мощность алфавита (N)
количество символов, используемых в алфавите
Например: 33
Информационный вес символа (i)
длина двоичного кода, с помощью которого кодируется символ алфавита
Например: 100101 - 6 битов
Повторение
Что такое:
Слайд 3Повторение
Формула определения информационного веса символа:
2i=M
Информационный объем текста:
I=K*i
Слайд 4Задача на повторение:
Сообщение, записанное буквами из 32-символьного алфавита, содержит 200
символов. Какой объем информации оно несет?
M=32, K=200, I=?
2i=M,
2i=32, i=5
I=K*i=
=200*5=1000 битов
Слайд 5Принцип: Чем больше первоначальная неопределенность знания, тем больше информации несет сообщение,
снимающее эту неопределенность.
Содержательный подход к измерению информации
Слайд 6Неопределенность знания о результате некоторого события (бросания монеты или игрального кубика, вытаскивание жребия и
др.) – это количество возможных результатов.
• Причем ни один из этих результатов не
имеет преимуществ перед другими.
• То есть они равновероятны.
Что такое неопределенность
знания?
Слайд 8Студент на экзамене может получить 2, 3, 4, 5 с одинаковой вероятностью. • Вы узнали, что
он
получил 4.
• Сколько бит
информации вы
получили?
Задача
Слайд 9Нужно задать наименьшее количество вопросов, ответами на которые могут быть только
слова «да» или «нет».
Метод половинного деления
ДА
НЕТ
?
Слайд 10Оценка выше тройки?
Да. Остались 4 и 5.
Вы получили 1 бит информации.
Оценка
5?
Нет. Осталось 4.
Вы получили еще 1 бит информации.
Вывод: сообщение об одном из четырех равновероятных событий несет 2 бита информации.
Вывод: сообщение об одном из четырех равновероятных событий несет 2 бита информации.
Метод половинного деления
Слайд 11Друг едет в одном из 8 вагонов поезда.
Сколько битов информации
несет сообщение о номере вагона?
Задача
Ответ: 3
Слайд 13Количество информации i, содержащееся в сообщении об одном из N равновероятных
исходов некоторого события, определяется из решения показательного уравнения:
2i=N
2i=N
Слайд 14В кинотеатре 256 мест. Какое количество информации несет сообщение о номере
вашего кресла?
2i=256=28
Получаем: i=8
2i=256=28
Получаем: i=8
Пример
Слайд 15i=log2N (логарифм от N по основанию 2)
Здесь i – количество информации,
содержащееся в сообщении об одном из N равновероятных исходов события
Формула Хартли
Ральф Хартли
(1888 — 1970)
американский учёный-электронщик
Слайд 16Если значение N не равно
целой степени двойки:
i=log2N (логарифм от N
по основанию 2)
Пр: log22=1, log24=2, log28=3
В случае с игральным кубиком N=6
i=log2N= log26= 2,584962501 (бита)
Пр: log22=1, log24=2, log28=3
В случае с игральным кубиком N=6
i=log2N= log26= 2,584962501 (бита)
Формула Хартли
Слайд 19После окончания работы нужно закрыть все активные программы. Рабочее место нужно
оставить чистым.
Не забывайте!!!
