- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему История систем счисления
Содержание
- 1. Презентация по информатике на тему История систем счисления
- 2. Системы счисления делятся:системы бирок (унарная, единичная);кодовые (непозиционные)
- 3. ПалочкаУзелокЗарубкаКамушекЭтим кодом пользуются малыши, показывая на пальцах
- 4. если количественный эквивалент значения каждого числа не
- 5. Умножить 15 на 24 1 24 2 48
- 6. Применялась более 2-х с половиной тысяч лет
- 7. В старину на Руси применялись системы счисления,
- 8. Постоянная потребность введения новых знаков для записи
- 9. если количественный эквивалент символа зависит от его
- 10. Начало положено в Древнем Египте и Вавилоне(цифры
- 11. Шестидесятеричная система счисления (1 час –
- 12. 1. Сравните VVV и 555. 2. Какие
- 13. Ответы1. VVV (5+5+5=15) < 5552. а) 1999
Слайд 1Исторические сведения
Системы счисления
Разработала:
Ногина Елена Михайловна
учитель информатики и ИКТ МБОУ
2019 год
Слайд 2Системы счисления делятся:
системы бирок (унарная, единичная);
кодовые (непозиционные) системы;
позиционные системы.
Система счисления -
Слайд 3Палочка
Узелок
Зарубка
Камушек
Этим кодом пользуются малыши, показывая на пальцах свой возраст.
Унарная система лежит
Унарная
система счисления
Слайд 4если количественный эквивалент значения каждого числа не зависит от его положения
Непозиционная
система счисления-
Математические текстуры, написанные 4000 лет назад в ДРЕВНЕМ ЕГИПТЕ.
Слайд 5Умножить 15 на 24
1 24
2 48
4 96
8 192
15=1+2+4+8,
15•24=360
Разделить 541 на 12
1 12
2 24
4 48
8 96
16 192
32 384
541 = 384+96+48+12+1
Значит получаем частное 32+8+4+1=45 и остаток 1
541:12=45 и остаток 1
Особую роль у египтян играло число 2 и его степень.
Умножение и деление они проводили путем последовательного удвоения и сложения чисел.
Древнеегипетскую систему счисления ученые относят к десятичным непозиционным
Слайд 6Применялась более 2-х с половиной тысяч лет назад в Древнем Риме.
I
V – раскрытая ладонь
X – две сложенные ладони
C – centum (латинское слово сто)
D – 500
M – mille (латинское слово тысяча).
Число разлагали на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятерок, единиц.
99 = XCIX (-10+100-1+10)
Римская
система счисления
Слайд 7В старину на Руси применялись системы счисления, отдаленно напоминающие римскую.
Слайд 8Постоянная потребность введения новых знаков для записи больших чисел.
Невозможно представить дробные
Сложно выполнить арифметические операции (нет определенных правил действий над числами).
Недостатки непозиционной системы счисления
Слайд 9если количественный эквивалент символа зависит от его положения в записи числа.
Французский математик
Пьер Симон Лаплас (1749-1827)
Позиционная
система счисления-
Слайд 10Начало положено в Древнем Египте и Вавилоне
(цифры 1, 2, 3, 4,
В V – VII вв. н. э. индийские математики ввели для пропуска разрядов обозначение нуля.
Арабы первыми познакомились с этой нумерацией, усвоили и перенесли в Европу.
В XII в. н. э. получила название арабская система счисления и распространилась по всей Европе.
Десятичная
система счисления
Слайд 11Шестидесятеричная система счисления (1 час – 60 минут; 1 минута –
1972 =_ _ _ | | _ _ _ _ _ | | (32∙60+52=1972)
Двенадцатеричная система счисления (12 – дюжина; в сутках – 2 дюжины, 1 час – 5 дюжин минут, 1 год – 12 месяцев, 1 фут – 12 дюжинов)
Другие позиционные
системы счисления
Слайд 121. Сравните VVV и 555.
2. Какие числа записаны римскими числами:
а) MCMXCIX
3. Выполните с помощью последовательного удвоений умножение чисел 48 и 15.
4. Разделите с помощью удвоений 1680 на 35.
5. Запишите в Вавилонской системе счисления год создания первой отечественной ЭВМ (1950г.)
Задания для закрепления
Слайд 13
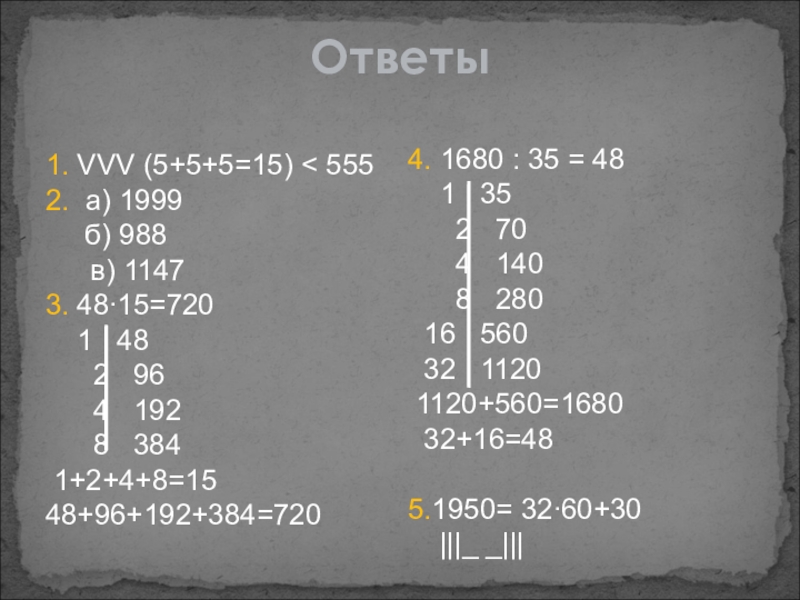
Ответы
1. VVV (5+5+5=15) < 555
2. а) 1999
б)
3. 48∙15=720
1 48
2 96
4 192
8 384
1+2+4+8=15
48+96+192+384=720
4. 1680 : 35 = 48
1 35
2 70
4 140
8 280
16 560
32 1120
1120+560=1680
32+16=48
5.1950= 32∙60+30
|||_ _|||