- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Имитационное моделирование
Содержание
- 1. Презентация по информатике на тему Имитационное моделирование
- 2. Имитационные модели (англ. simulation models) – один из
- 3. Признаки имитационной моделиОбъект моделирования – система, состоящая
- 4. Примеры имитационного моделирования:Броуновское движениеОбъект моделирования: броуновская частицаСлучайные
- 5. Примеры имитационного моделированияДинамика популяций;Политические выборы;Обслуживание очередей
- 6. Математический аппарат имитационного моделированияОснову математического аппарата имитационного
- 7. Если вероятности известны, то говорят, что задано
- 8. Плотность вероятностиСлучайная величина может быть непрерывной, если
- 9. Характерные распределения случайных величин- Равномерное распределениеP(x)xabПлотность вероятности равномерного распределения.Формулы равномерно распределения:
- 10. Нормальное распределение – распределение Гауса-∞
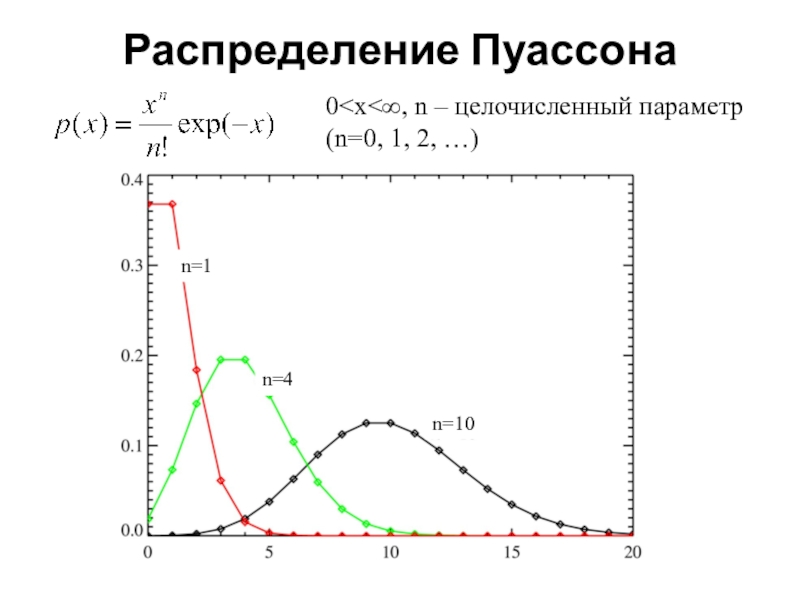
- 11. Распределение Пуассона0
- 12. Оценка вероятностных характеристик случайного процессаВыборка - это
Слайд 1Имитационное моделирование
Методика имитационного моделирования.
Математический аппарат имитационного моделирования
Слайд 2Имитационные модели (англ. simulation models) – один из основных классов математического моделирования.
Целью построения имитаций является максимальное приближение модели к конкретному (чаще всего уникальному) экологическому объекту и достижение максимальной точности его описания.
Имитационные модели претендуют на выполнение как объяснительных, так и прогнозных функций.
Слайд 3Признаки имитационной модели
Объект моделирования – система, состоящая из множества взаимодействующих элементов.
Состояния
Известны правила взаимодействия элементов, определяемые физическими, биологическими , экономическими и другими законами.
Метод – пошаговое описание изменения состояния элементов системы.
Существуют интегральные характеристики состояния системы.
Цель моделирования – оценка изменения со временем интегральных характеристик системы через отслеживание всех актов взаимодействия элементов системы.
Слайд 4Примеры имитационного моделирования:
Броуновское движение
Объект моделирования: броуновская частица
Случайные факторы: положение молекул в
Правила взаимодействия: закон сохранения импульса.
Интегральные характеристики: координаты и скорость броуновской частицы; температура среды.
Метод расчета: с малым шагом по времени рассчитываются изменения координат броуновской частицы.
Цель моделирования: описание траектории и скорости перемещения броуновской частицы в зависимости от температуры.
Слайд 5Примеры имитационного моделирования
Динамика популяций;
Политические выборы;
Обслуживание очередей
Слайд 6Математический аппарат имитационного моделирования
Основу математического аппарата имитационного моделирования составляют теория вероятностей
Понятие вероятности в математике определяется так:
Вероятность равна отношению числа исходов, благоприятствующих данному событию, к общему числу равновозможных исходов.
Значение вероятности лежит в диапазоне от 0 до 1
Слайд 7Если вероятности известны, то говорят, что задано распределение случайной величины Х
Характеристики
Среднее значение
- Дисперсия
Если дисперсия равна нулю, то это значит, что случайная величина принимает
единственное возможное значение , т.е. не является случайной.
Большая дисперсия указывает на большое рассеивание случайной величины.
Слайд 8Плотность вероятности
Случайная величина может быть непрерывной, если её возможными значениями являются
Для непрерывно распределенной случайной величины x большую роль в её описании играет функция распределения плотности вероятности p(x)
Содержательный смысл p(x)
ДЛЯ ВСЯКОЙ ТОЧКИ И ВЗЯТОГО ОКОЛО НЕЕ МАЛОГО ОТРЕЗКА ∆X ПРОИЗВЕДЕНИЕ P(X0)∆X РАВНО ВЕРОЯТНОСТИ ТОГО, ЧТО СЛУЧАЙНАЯ ПЕРЕМЕННАЯ ПРИМЕТ ЗНАЧЕНИЕ, ЗАКЛЮЧЕННОЕ МЕЖДУ Х0 И Х0+ ∆X .
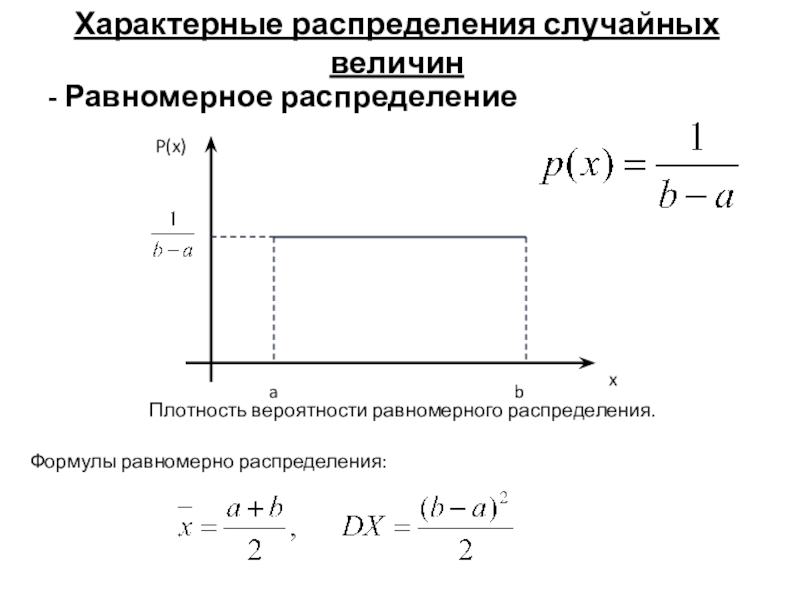
Слайд 9Характерные распределения случайных величин
- Равномерное распределение
P(x)
x
a
b
Плотность вероятности равномерного распределения.
Формулы равномерно распределения:
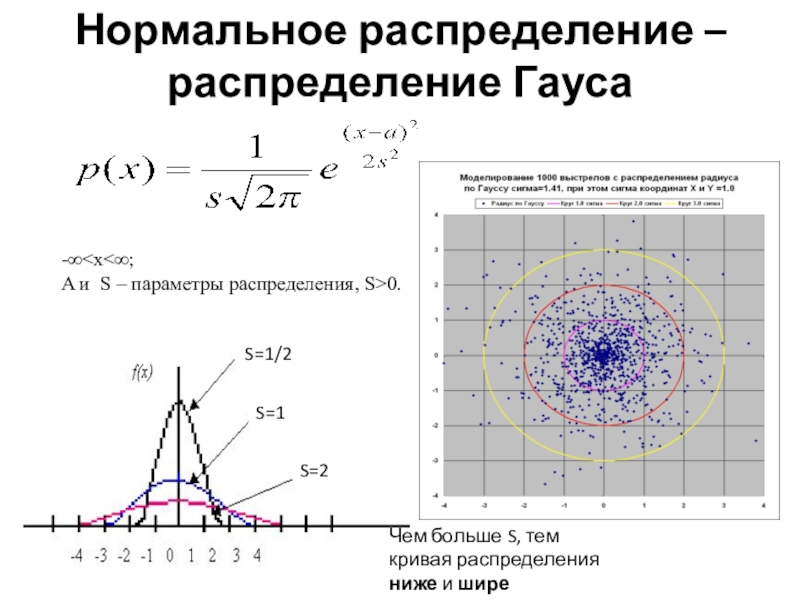
Слайд 10Нормальное распределение – распределение Гауса
-∞
Чем больше S, тем кривая распределения ниже и шире
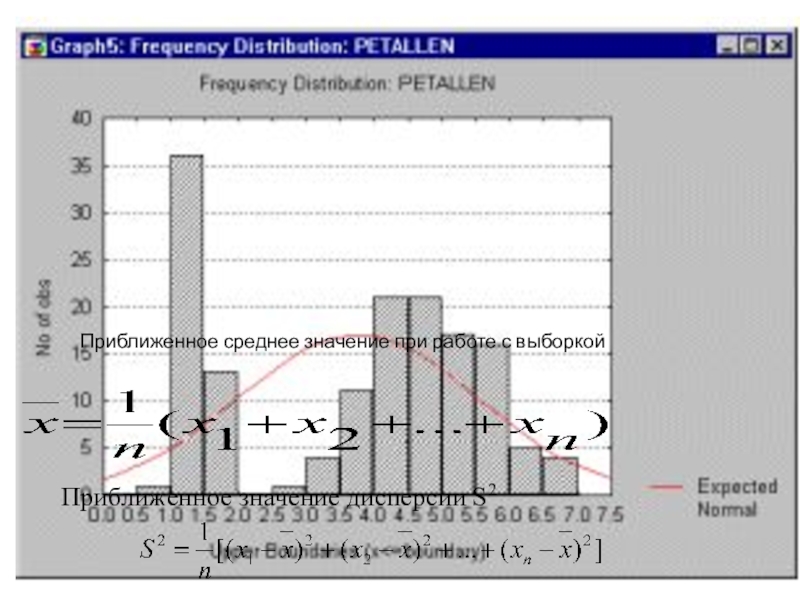
Слайд 12Оценка вероятностных характеристик случайного процесса
Выборка - это множество исходов каких-либо однородных
По результатам выборки могут решаться разные задачи:
Сделать заключение о том, какой вид имеет функция распределения величины Х
Если невозможно решение первой задачи, то хотя бы определить значение наиболее часто используемых параметров распределения, таких как среднее значение и дисперсия.
Приближенное значение дисперсии S2