- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Двоичная и десятичная система счисления
Содержание
- 1. Презентация по информатике на тему Двоичная и десятичная система счисления
- 2. Десятичная и двоичная системы счисления Системой счисления
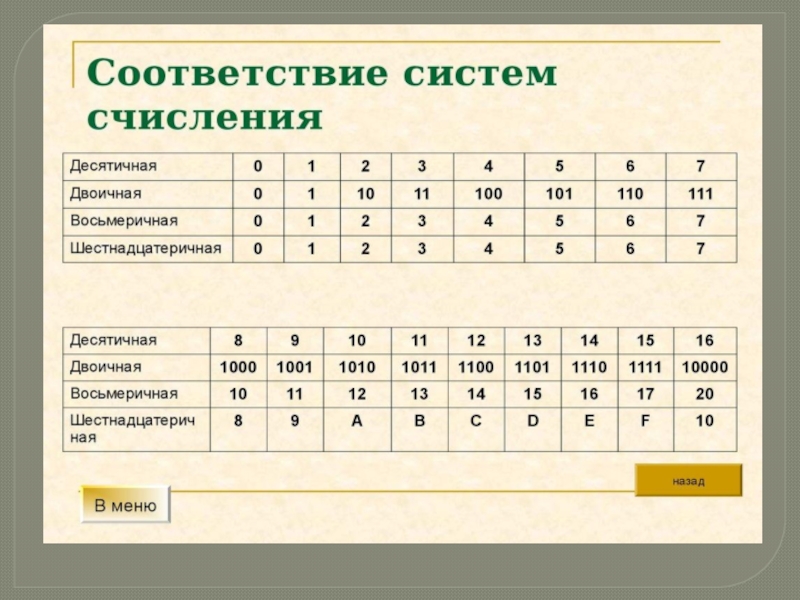
- 3. Слайд 3
- 4. Почему двоичная система счисления так распространена.Дело в
- 5. Перевод десятичного числа в двоичное.Может потребоваться перевести
- 6. Слайд 6
- 7. Двоичная и десятичная система счисления.В двоичной системе
- 8. Примеры:Попробуем считать в двоичной системе: 0 –
- 9. Примеры десятичной:В десятичной системе счисления любое число
- 10. Слайд 10
- 11. Интересные факты:Десятичная система счисления пришла из древней
- 12. Слайд 12
- 13. Сп
Десятичная и двоичная системы счисления Системой счисления называют определенные правила записи чисел и связанные с ними способы выполнения вычислений. Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются
Слайд 2Десятичная и двоичная системы счисления
Системой счисления называют определенные правила записи
чисел и связанные с ними способы выполнения вычислений.
Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число цифр определяет основание системы счисления. Если число цифр — десять, то основание системы счисления равно десяти. В двоичной же системе существует всего две цифры: 0 и 1. Основание равно двум. Возникает вопрос, можно ли с помощью всего двух цифр представить любую величину. Оказывается, можно!
Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число цифр определяет основание системы счисления. Если число цифр — десять, то основание системы счисления равно десяти. В двоичной же системе существует всего две цифры: 0 и 1. Основание равно двум. Возникает вопрос, можно ли с помощью всего двух цифр представить любую величину. Оказывается, можно!
Слайд 4Почему двоичная система счисления так распространена.
Дело в том, что двоичная система
счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Слайд 5Перевод десятичного числа в двоичное.
Может потребоваться перевести десятичное число в двоичное.
Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток) 38 / 2 = 19 (0 остаток) 19 / 2 = 9 (1 остаток) 9 / 2 = 4 (1 остаток) 4 / 2 = 2 (0 остаток) 2 / 2 = 1 (0 остаток) 1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
77 / 2 = 38 (1 остаток) 38 / 2 = 19 (0 остаток) 19 / 2 = 9 (1 остаток) 9 / 2 = 4 (1 остаток) 4 / 2 = 2 (0 остаток) 2 / 2 = 1 (0 остаток) 1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Слайд 7Двоичная и десятичная система счисления.
В двоичной системе счисления используются всего две
цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Слайд 8Примеры:
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один
(и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Слайд 9Примеры десятичной:
В десятичной системе счисления любое число можно представить в форме
суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 - это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 - это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Слайд 11Интересные факты:
Десятичная система счисления пришла из древней Индии, там впервые стали
использовать «0».
В Европе об этой системе узнали в 12 веке из арабских научных трактов, которые были переведены на латынь. Этим и объясняется название «Арабские цифры».
Предполагается, что основание 10 связано с количеством пальцев на руках.
Самой старой системой счисления является
двоичная. Эта система обладает рядом качеств, делающей ее очень выгодной и необходимой в использовании в телеграфах, а также в вычислительных машинах и в современных компьютерах.
В Европе об этой системе узнали в 12 веке из арабских научных трактов, которые были переведены на латынь. Этим и объясняется название «Арабские цифры».
Предполагается, что основание 10 связано с количеством пальцев на руках.
Самой старой системой счисления является
двоичная. Эта система обладает рядом качеств, делающей ее очень выгодной и необходимой в использовании в телеграфах, а также в вычислительных машинах и в современных компьютерах.