- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Алгоритмы обработки информации 10 класс
Содержание
- 1. Презентация по информатике на тему Алгоритмы обработки информации 10 класс
- 2. алгоритмисполнитель алгоритмасвойства алгоритмадискретностьдетерминированностьпонятностьрезультативностьконечностьмассовость вычислительный процесссложность алгоритма
- 3. Художник Василий Тропинин «Золотошвейка» (1826)понимает смысл алгоритма,
- 4. Понятие алгоритмаАлгоритм – точная система предписаний, определяющая
- 5. Пример 1 Исполнитель: человекОбъекты алгоритма: ключ, дверьАлгоритм
- 6. Пример 2Алгоритм «Нахождение всех простых чисел не
- 7. Пример 2Алгоритм «Нахождение всех простых чисел не
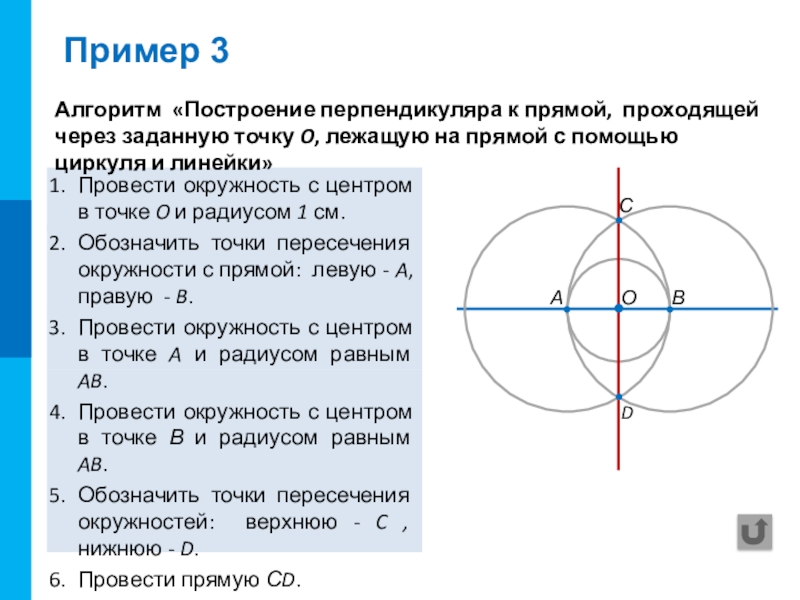
- 8. Пример 3Алгоритм «Построение перпендикуляра к прямой, проходящей
- 9. Пример 3Алгоритм «Построение перпендикуляра к прямой, проходящей
- 10. Свойства алгоритмаДискретностьДетерминированностьПонятностьРезультативностьМассовостьДискретностьВыполнение алгоритма разбивается на последовательность законченных
- 11. Давайте обсудимМожно ли кулинарный рецепт считать алгоритмом? Ответ обоснуйте с точки зрения свойств алгоритма.?
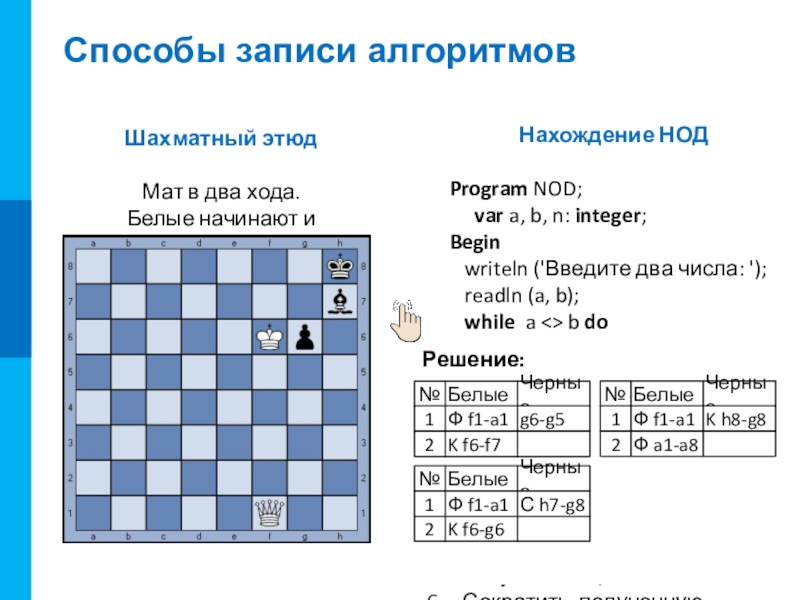
- 12. Способы записи алгоритмовсловесная запись алгоритма на
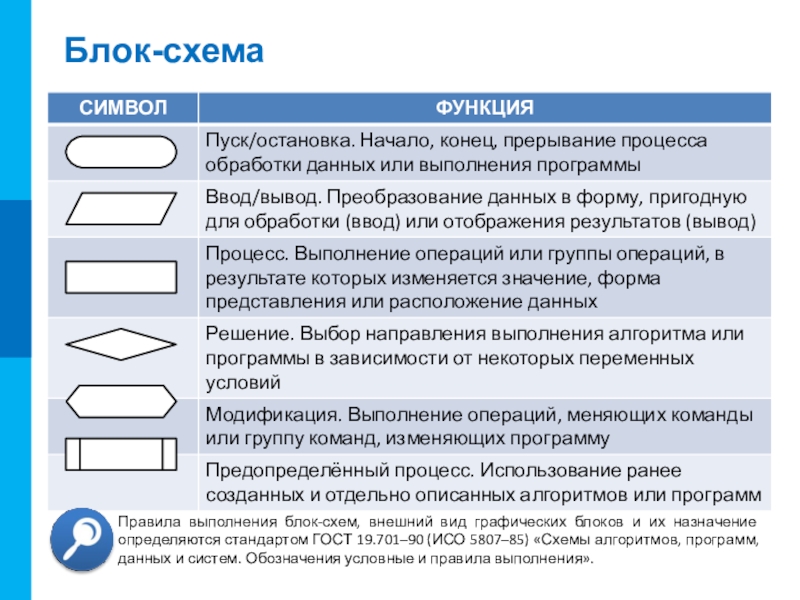
- 13. Правила выполнения блок-схем, внешний вид графических блоков
- 14. Понятие сложности алгоритмаТеория алгоритмов предоставляет аппарат анализа
- 15. Временная сложность«Найти книгу с секретом»Сложность алгоритма выражают
- 16. Пример 4 Алгоритм «Возведение числа в натуральную
- 17. Алгоритм – конечная система правил, сформулированных на
- 18. Алгоритм состоит из команд. Команда – отдельная
- 19. Вопросы и заданияЗадание 1. Автомат получает на
- 20. Вопросы и заданияЗадание 2. Подсчитайте сложность алгоритма
- 21. 833333Вопросы и заданияЗадание 1. Есть двое песочных
- 22. Информационные источникиhttps://img2.goodfon.ru/original/1920x1080/a/91/zamok-klyuch-otverstie-svet.jpghttp://biblo-ok.ru/biblio-ok/Kartiny1/79.files/image001.jpghttp://cheeseberry-sibir.ru/photos/vyshivka-na-odejde-izgotovlenie-6259-large.jpghttp://europeansectionarcipreste.blogspot.ru/2011_11_01_archive.htmlhttp://www.imasitalia.com/wp-content/uploads/2016/04/fogli.jpg http://atotarho12.narod.ru/clipart/k/kar/karanda44.pnghttps://s-media-cache-ak0.pinimg.com/originals/73/96/fd/7396fd0a921a5f895bafd81830adcaa5.jpghttps://chessok.net/zadachi/1165-reshit-legkuyu-dvuhhodovku.htmlhttp://pikabu.ru/story/metod_byistrogo_umnozheniya_karatsubyi_4226758http://ozon.ru. Сейф-книга "Вид на реку"https://openclipart.org/image/800px/svg_to_png/171487/1344190891.pnghttp://vamotkrytka.ru/_ph/54/2/531435092.gifhttp://www.gifmania.ru/Animated-Gifs-Veb-dizayn/Animations-Geometry/Images-Geometric-Stars/Geometric-Stars-89830.gifhttp://www.freeiconspng.com/free-images/potion-icon-png-15620
Слайд 2алгоритм
исполнитель алгоритма
свойства алгоритма
дискретность
детерминированность
понятность
результативность
конечность
массовость
вычислительный процесс
сложность алгоритма
Слайд 3Художник Василий Тропинин «Золотошвейка» (1826)
понимает смысл алгоритма, может его корректировать и
одну и ту же команду выполняет каждый раз по-разному
неформальный исполнитель сам отвечает за свои действия
в роли неформального исполнителя чаще всего выступает человек
Исполнитель алгоритма
Исполнитель алгоритма – это субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить содержащийся в нём перечень действий.
!
не размышляет над выполняемыми командами, а строго следует пошаговым инструкциям алгоритма
одну и ту же команду всегда выполняет одинаково
за действия формального исполнителя отвечает управляющий им объект
в роли формального исполнителя чаще всего выступает техническое устройство
Неформальный
исполнитель
Формальный
исполнитель
Слайд 4Понятие алгоритма
Алгоритм – точная система предписаний, определяющая содержание и порядок действий
!
ПРИМЕРЫ АЛГОРИТМОВ
Закрыть
входную дверь ключом
Нахождение n первых простых чисел
(метод Эратосфена)
Построение перпендикуляра
к прямой
Слайд 5Пример 1
Исполнитель: человек
Объекты алгоритма: ключ, дверь
Алгоритм
«Закрыть входную дверь ключом»
Вставить
Повернуть ключ два раза на 180 градусов против часовой стрелки.
Вынуть ключ из замочной скважины.
Слайд 6Пример 2
Алгоритм «Нахождение всех простых чисел не больше заданного числа n
Выписать подряд все целые числа от 2 до n (2, 3, 4, …, n).
Присвоить переменной p значение 2 (2 – первое простое число).
Зачеркнуть в списке числа, кратные p: 2p, 3p, 4p, …
Найти первое незачёркнутое число в списке, большее чем p, и присвоить p соответствующее значение.
Повторять шаги 3 и 4, пока возможно (пока p2 ≤ n).
Незачёркнутые числа и есть все простые числа от 2 до n.
Простые числа от 2 до 100
Выполнить
Слайд 7Пример 2
Алгоритм «Нахождение всех простых чисел не больше заданного числа n
Простые числа от 2 до 100
p = 2
p = 3
p = 5
p = 7
Выписать подряд все целые числа от 2 до n (2, 3, 4, …, n).
Присвоить переменной p значение 2 (2 – первое простое число).
Удалить из списка числа, кратные p: 2p, 3p, 4p, …
Найти первое число в списке, большее чем p, и присвоить p соответствующее значение.
Повторять шаги 3 и 4, пока возможно (пока p2 ≤ n).
Оставшиеся числа и есть все простые числа от 2 до n.
Слайд 8Пример 3
Алгоритм «Построение перпендикуляра к прямой, проходящей через заданную точку O,
Выполнить
Провести окружность с центром в точке O и радиусом 1 см.
Обозначить точки пересечения окружности с прямой: левую - A, правую - B.
Провести окружность с центром в точке A и радиусом равным AB.
Провести окружность с центром в точке В и радиусом равным AB.
Обозначить точки пересечения окружностей: верхнюю - C, нижнюю - D.
Провести прямую СD.
Слайд 9Пример 3
Алгоритм «Построение перпендикуляра к прямой, проходящей через заданную точку O,
О
А
В
С
D
Провести окружность с центром в точке O и радиусом 1 см.
Обозначить точки пересечения окружности с прямой: левую - A, правую - B.
Провести окружность с центром в точке A и радиусом равным AB.
Провести окружность с центром в точке В и радиусом равным AB.
Обозначить точки пересечения окружностей: верхнюю - C , нижнюю - D.
Провести прямую СD.
Слайд 10Свойства алгоритма
Дискретность
Детерминированность
Понятность
Результативность
Массовость
Дискретность
Выполнение алгоритма разбивается на последовательность законченных действий-шагов. Только выполнив одно
Детерминированность
Каждая команда алгоритма определяет однозначное действие исполнителя, и недвусмысленно указывает, какая команда должна выполняться следующей. Многократное выполнение алгоритма при одном и том же наборе входных данных, дает одинаковые промежуточные и выходной результаты.
Понятность
Алгоритм не должен содержать предписаний, смысл которых может восприниматься исполнителем неоднозначно, т. е. запись алгоритма должна быть настолько чёткой и полной, чтобы у исполнителя не возникло потребности в принятии каких-либо самостоятельных решений.
Результативность
При точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть установление того факта, что задача решений не имеет.
Массовость
Алгоритм пригоден для решения любой задачи из некоторого класса задач, т. е. алгоритм правильно работает на некотором множестве исходных данных, которое называется областью применимости алгоритма.
Алгоритм – конечная система правил, сформулированных на языке исполнителя, которая определяет последовательность перехода от допустимых исходных данных к конечному результату и обладает свойствами дискретности, детерминированности, понятности, результативности, конечности и массовости.
!
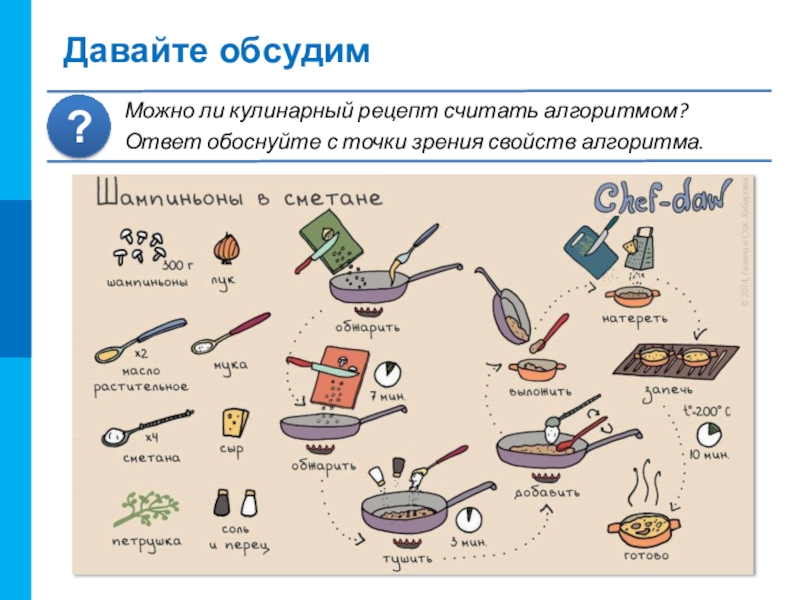
Слайд 11Давайте обсудим
Можно ли кулинарный рецепт считать алгоритмом?
Ответ обоснуйте с точки
?
Слайд 12Способы записи алгоритмов
словесная запись алгоритма
на естественном языке
запись алгоритма на языке
с помощью блок-схемы –
стандартных графических объектов
(геометрических фигур)
запись алгоритма с помощью
формул, рисунков, таблиц
Слайд 13Правила выполнения блок-схем, внешний вид графических блоков и их назначение определяются
Блок-схема
Слайд 14Понятие сложности алгоритма
Теория алгоритмов предоставляет аппарат анализа различных алгоритмов решения одной
Вычислительным процессом, порождённым алгоритмом, называется последовательность шагов алгоритма, пройденных при его исполнении.
Сложность алгоритма – количество элементарных шагов (действий) в вычислительном процессе этого алгоритма.
!
Для решения задачи могут быть разработаны алгоритмы, имеющие разную сложность. Лучшим среди них считается алгоритм, имеющий наименьшую сложность.
Эффективность оценивается количеством элементарных операций, которые необходимо выполнить для решения задачи, а также количеством памяти, требующейся для выполнения алгоритма.
Слайд 15Временная сложность
«Найти книгу с секретом»
Сложность алгоритма выражают в виде функции от
Задание. Оцените сложность алгоритмов:
Сложность алгоритма будет O(log2n).
Таким образом, в книге объёмом в 1000 страниц страница с нужной фамилией находится не больше, чем за O(log21000) ≈ 10 раз.
В данном случае, за счет сортировки имен по алфавиту, можно сократить поиск, применив метод половинного деления (открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое).
При линейном поиске – последовательной проверки всех книг подряд – сложность, в худшем случае, будет равна количеству книг, т.е. O(n) = 1000.
В старинной библиотеке в одном из 1000 томов, посвященных кладам и тайникам, спрятана книга-сейф. Надо найти ее.
Слайд 16Пример 4
Алгоритм «Возведение числа в натуральную степень (xn)»
Запишем n
Заменим каждую 1 парой букв КХ, а каждый 0 – буквой К.
Вычеркнем крайнюю левую пару КХ.
Полученная строка, читаемая слева направо, даёт правило быстрого вычисления хn, если букву К рассматривать как операцию возведения результата в квадрат, а букву X – как операцию умножения результата на х. Вначале результат равен х.
К
К
Х
К
К
К
х2
х4
х5
х10
х20
х40
Слайд 17Алгоритм – конечная система правил, сформулированных на языке исполнителя, которая определяет
Исполнитель алгоритма – субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить содержащийся в нём перечень действий.
Один и тот же алгоритм может быть записан разными способами: на естественном языке, псевдокодом, с помощью блок-схем, на языке программирования и т. д.
Теория алгоритмов предоставляет аппарат анализа различных алгоритмов решения одной и той же задачи, на основе которого можно выбрать самый эффективный (наилучший) алгоритм.
Слайд 18Алгоритм состоит из команд. Команда – отдельная инструкция в описании алгоритма.
Сложность алгоритма – количество элементарных шагов (действий) в вычислительном процессе этого алгоритма. Наряду со сложностью важной характеристикой алгоритма является эффективность. Эффективность оценивается количеством элементарных операций, которые необходимо выполнить для решения задачи, а также количеством памяти, требующейся для выполнения алгоритма.
Слайд 19Вопросы и задания
Задание 1. Автомат получает на вход трёхзначное число. По
Складываются первая и вторая, а также вторая и третья цифры исходного числа.
Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Укажите наименьшее число, в результате обработки которого автомат выдаст число 1711.
Решение:
Единственный способ разбить запись 1711 на два числа – это 17 и 11.
Чтобы число было меньше, надо чтобы сумма первой и второй цифр была наименьшей, в данном случае 11.
Сумма значений двух последних цифр равна 17. Не трудно заметить, что 17 = 8 + 9 = 9 + 8. Других вариантов нет.
Тогда 11 = 2 + 9 = 3 + 8. Выбираем пару, которая даст меньшее число.
Ответ: 298.
Слайд 20Вопросы и задания
Задание 2. Подсчитайте сложность алгоритма сложения двух натуральных чисел
Решение:
Сложение двух чисел столбиком в случае, если одно из них состоит из n, а другое – из m цифр требует не более max(n, m) сложений и не более max(n, m) запоминаний (в случае перехода через десяток).
Т.е. данный алгоритм имеет сложность порядка O(n+m).
Выражение показывает только порядок величины – постоянные факторы в нем не учитываются.
Слайд 218
3
3
3
3
3
Вопросы и задания
Задание 1. Есть двое песочных часов: на 3 и
Графический способ решения: