- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Алгебра логики
Содержание
- 1. Презентация по информатике на тему Алгебра логики
- 2. Формальная логика - наука, позволяющая делать заключения
- 3. Закон исключения третьего«Во время своих странствий Платон
- 4. Закон непротиворечивости«Во время своих странствий Платон был в Египте И не был Платон в Египте»Формальная логика
- 5. Закон отрицания«Если не верно, что Платон НЕ
- 6. Высказывание- это основной элемент логики, определяемый как
- 7. Какие из предложений могут быть высказыванием?Листья опадают осеньюЗемля прямоугольная2>1Не пейте сырую водуКто не хочет быть счастливымH2O+SO3=H2SO4
- 8. Алгебра логикиДжордж Буль, 1847 г1 – высказывание истинно0 – высказывание ложно
- 9. Инверсия (логическое отрицание)Обозначение:, ¯, Не верно, что…Черное – белоеДа – НетИстинно - Ложно
- 10. Конъюнкция (логическое умножение)Обозначение: , &, ИНа
- 11. Дизъюнкция (логическое сложение)Обозначение: , ИЛИНа стоянке
- 12. Строгая дизъюнкция Обозначение: , ИЛИ … ИЛИ
- 13. Импликация (логическое следование)Обозначение: , ЕСЛИ… ТО…ЕСЛИ
- 14. Эквивалентность (логическое равенство)Обозначение: , ТОГДА И ТОЛЬКО
Формальная логика - наука, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения.
Слайд 2Формальная логика
- наука, позволяющая делать заключения о правильности какого-либо суждения
не по его фактическому содержанию, а только по форме его построения.
Слайд 3Закон исключения третьего
«Во время своих странствий Платон был в Египте ИЛИ
не был Платон в Египте»
Формальная логика
Слайд 4Закон непротиворечивости
«Во время своих странствий Платон был в Египте И не
был Платон в Египте»
Формальная логика
Слайд 5Закон отрицания
«Если не верно, что Платон НЕ был в Египте, то
значит Платон был в Египте»
Формальная логика
Слайд 6Высказывание
- это основной элемент логики, определяемый как повествовательное предложение, относительно которого
можно однозначно сказать истинно оно или ложно
Формальная логика
Слайд 7Какие из предложений могут быть высказыванием?
Листья опадают осенью
Земля прямоугольная
2>1
Не пейте сырую
воду
Кто не хочет быть счастливым
H2O+SO3=H2SO4
Кто не хочет быть счастливым
H2O+SO3=H2SO4
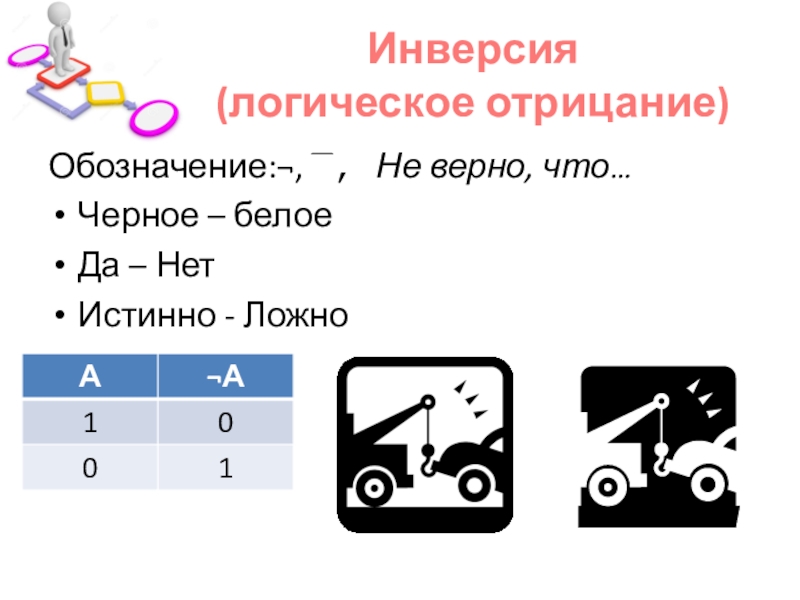
Слайд 9Инверсия
(логическое отрицание)
Обозначение:, ¯, Не верно, что…
Черное – белое
Да – Нет
Истинно -
Ложно
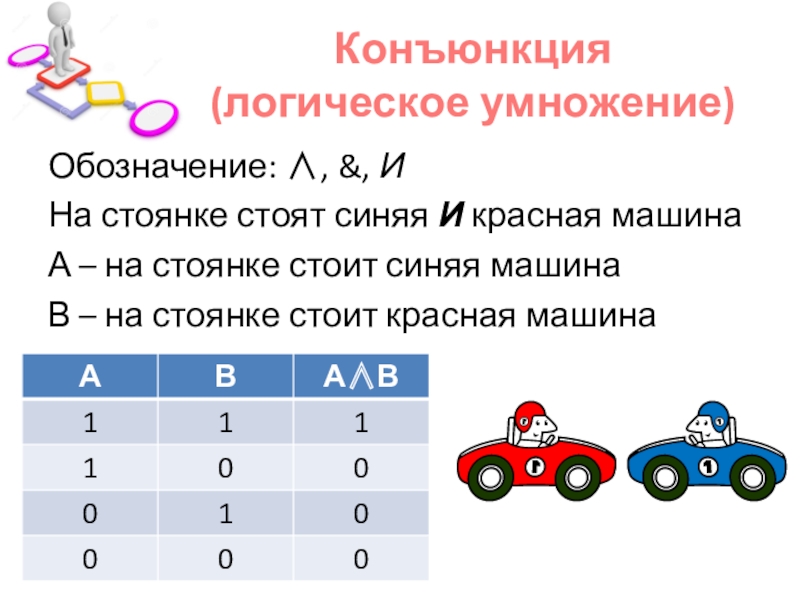
Слайд 10Конъюнкция
(логическое умножение)
Обозначение: , &, И
На стоянке стоят синяя И красная
машина
А – на стоянке стоит синяя машина
В – на стоянке стоит красная машина
А – на стоянке стоит синяя машина
В – на стоянке стоит красная машина
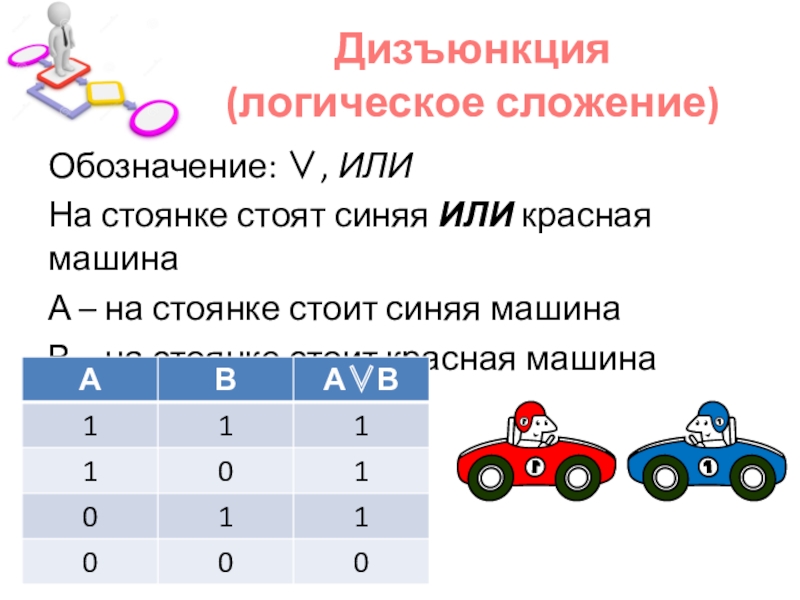
Слайд 11Дизъюнкция
(логическое сложение)
Обозначение: , ИЛИ
На стоянке стоят синяя ИЛИ красная машина
А
– на стоянке стоит синяя машина
В – на стоянке стоит красная машина
В – на стоянке стоит красная машина
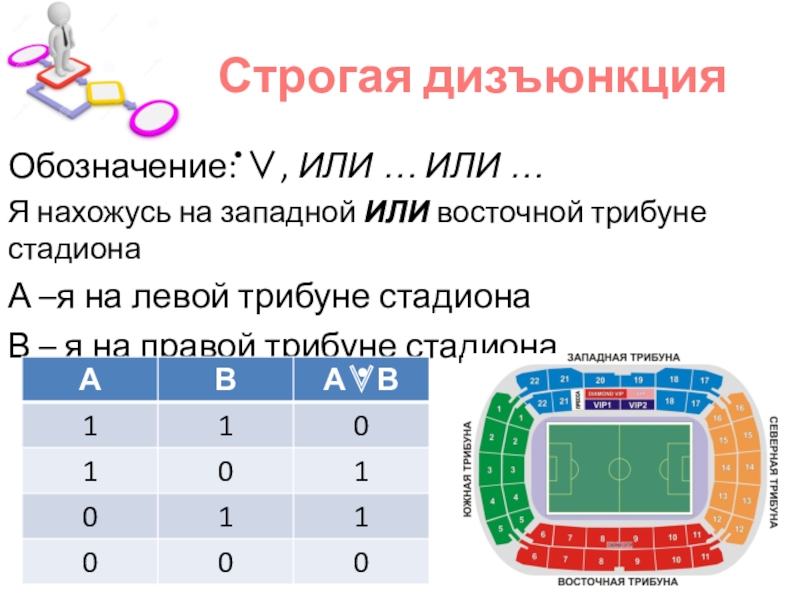
Слайд 12Строгая дизъюнкция
Обозначение: , ИЛИ … ИЛИ …
Я нахожусь на западной
ИЛИ восточной трибуне стадиона
А –я на левой трибуне стадиона
В – я на правой трибуне стадиона
А –я на левой трибуне стадиона
В – я на правой трибуне стадиона
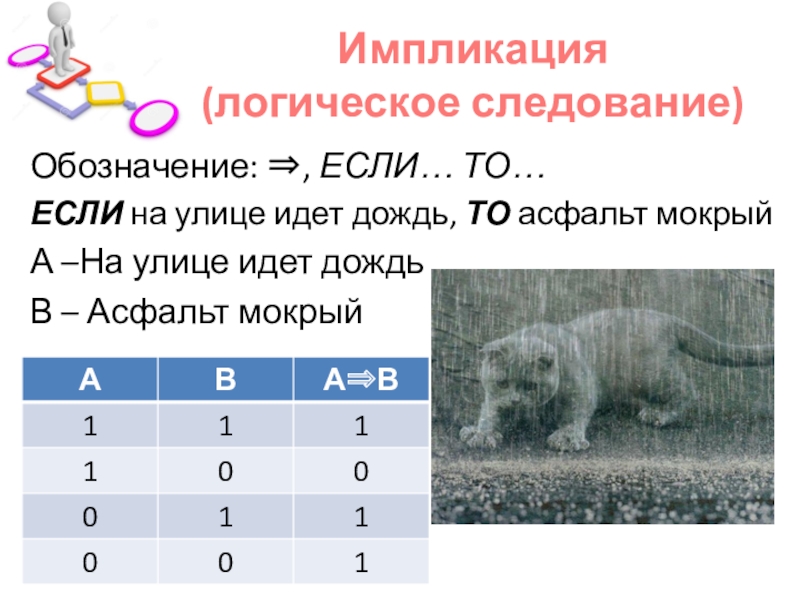
Слайд 13Импликация
(логическое следование)
Обозначение: , ЕСЛИ… ТО…
ЕСЛИ на улице идет дождь, ТО
асфальт мокрый
А –На улице идет дождь
В – Асфальт мокрый
А –На улице идет дождь
В – Асфальт мокрый
Слайд 14Эквивалентность
(логическое равенство)
Обозначение: , ТОГДА И ТОЛЬКО ТОГДА, КОГДА
Число делится на 3
ТОГДА И ТОЛЬКО ТОГДА, КОГДА сумма цифр делится на 3
А –число делится на 3
В – сумма цифр делится на 3
А –число делится на 3
В – сумма цифр делится на 3