- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Алгебра логики
Содержание
- 1. Презентация по информатике на тему Алгебра логики
- 2. Логика – это наука о формах и законах человеческого мышления.
- 3. ЛогикаДжордж Буль (1815-1864). Создал новую область науки
- 4. Алгебра логики (булева алгебра) - это раздел
- 5. высказывания
- 6. Логическое высказывание – это повествовательное предложение, относительно
- 7. Виды высказываний
- 8. Высказывание называется простым, если никакая его часть
- 9. Так, например, из элементарных высказываний "Петров —
- 10. При помощи связки "или" из этих же
- 11. В алгебре логики высказывания обозначают ЗАГЛАВНЫМИ буквами
- 12. Так, например, предложение " Трава зеленая" следует
- 13. Пусть через А обозначено высказывание "Тимур поедет
- 14. Тогда составное высказывание "Тимур летом побывает
- 15. A – Сейчас идет дождь.B – Форточка
- 16. Операции над логическими высказываниями
- 17. Операция НЕ Операция, выражаемая словом "не",
- 18. Высказывание А истинно, когда A ложно, и
- 19. 1001таблица истинности операции НЕТаблица истинности логического выражения
- 20. Операция И Операция, выражаемая связкой "и",
- 21. Высказывание А · В истинно тогда и
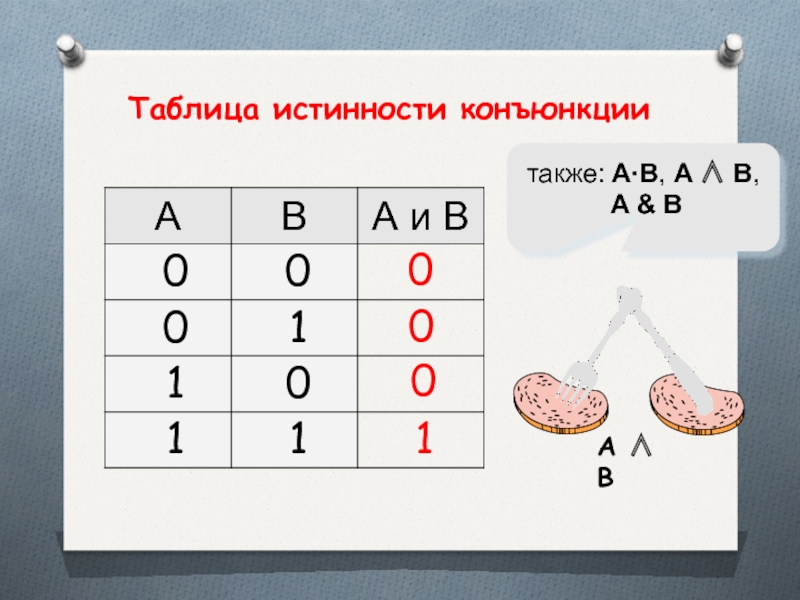
- 22. 10также: A·B, A ∧ B, A & B 00A ∧ BТаблица истинности конъюнкции
- 23. Операция ИЛИ Операция, выражаемая связкой "или"
- 24. Высказывание А v В ложно тогда и
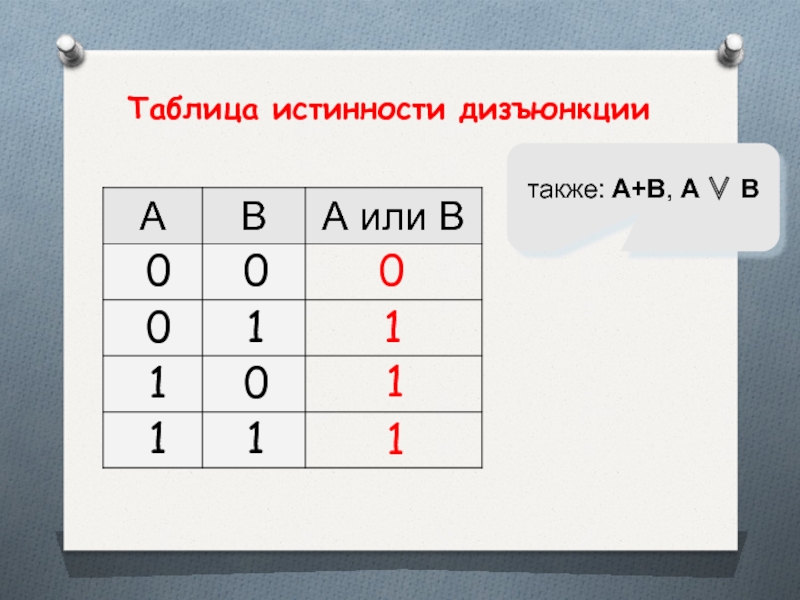
- 25. 10также: A+B, A ∨ B 11Таблица истинности дизъюнкции
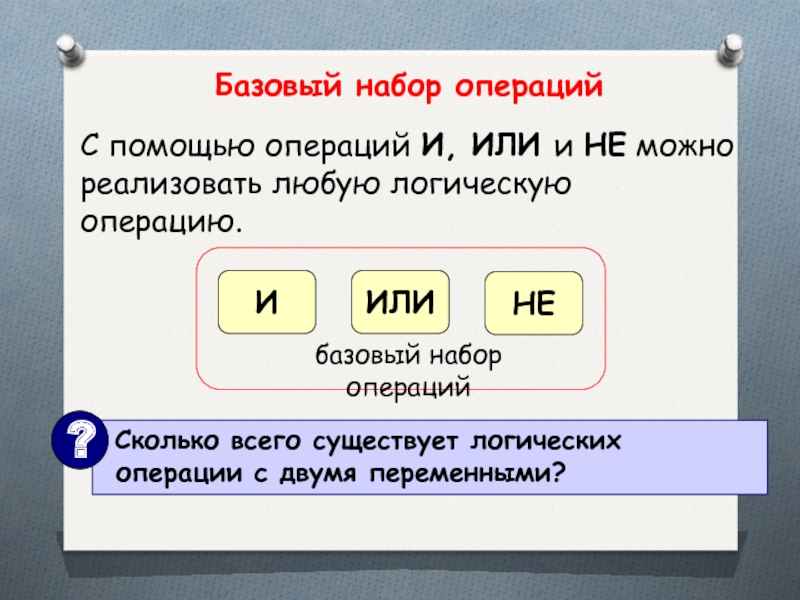
- 26. Базовый набор операцийС помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 27. Операция ЕСЛИ-ТО Операция, выражаемая связками
- 28. A – "Работник хорошо работает". B – "У работника хорошая зарплата".1110Таблица истинности импликации
- 29. Операция РАВНОСИЛЬНО Операция, выражаемая связками "тогда
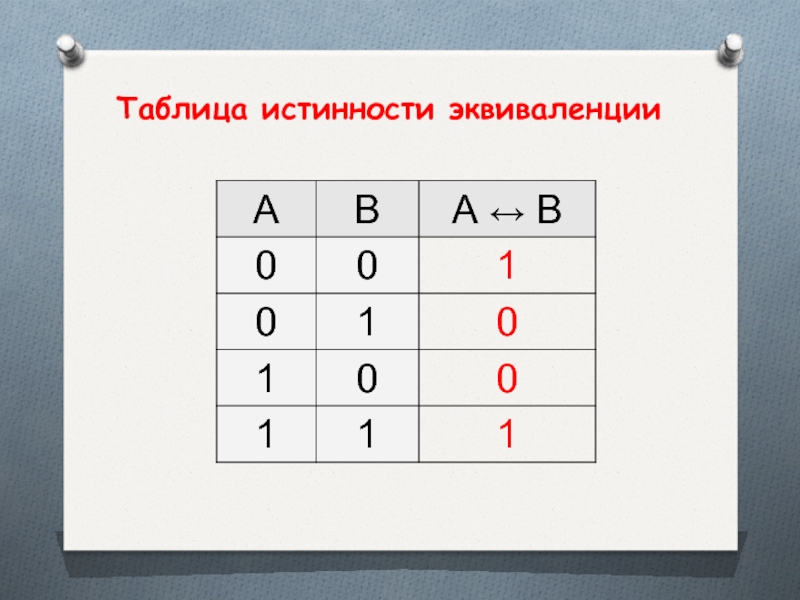
- 30. Таблица истинности эквиваленции
- 31. С помощью логических переменных и символов логических
- 32. Определение логической формулы: 1. Всякая логическая переменная
- 33. Порядок выполнения логических операций в сложном логическом выражении1.Инверсия; 2. Конъюнкция; 3. Дизъюнкция; 4. Импликация; 5. Эквивалентность.
- 34. Определите истинность составного высказывания: (А&В) & (C\/D),
- 35. Даны простые высказывания:А = {Принтер – устройство
- 36. Логические выражения и их таблицы истинности Составные высказывания
- 37. Таблица истинности - это табличное представление логической
- 38. Построение таблиц истинности для логических выраженийподсчитать n
- 39. А V A & Bn (число переменных)
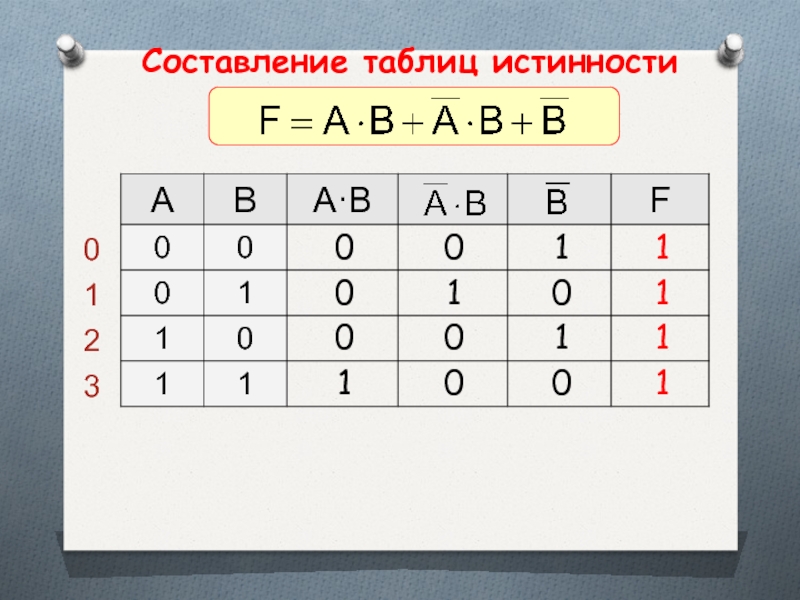
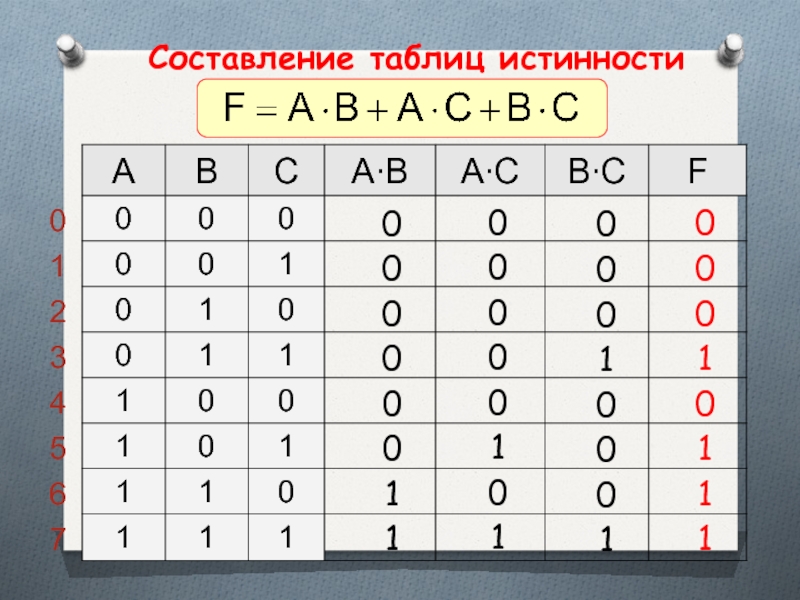
- 40. Составление таблиц истинности
- 41. Составление таблиц истинности
- 42. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
- 43. Закон тождестваA = AЗакон тождества означает, что
- 44. Закон непротиворечияA & notA = 0Не могут
- 45. Закон исключения третьегоA and not A =
- 46. Закон двойного отрицания Not (notA)=1Если отрицать дважды
- 47. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ КОМПЬЮТЕРА
- 48. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.
- 49. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие.
- 50. Каждый логический элемент имеет свое условное обозначение,
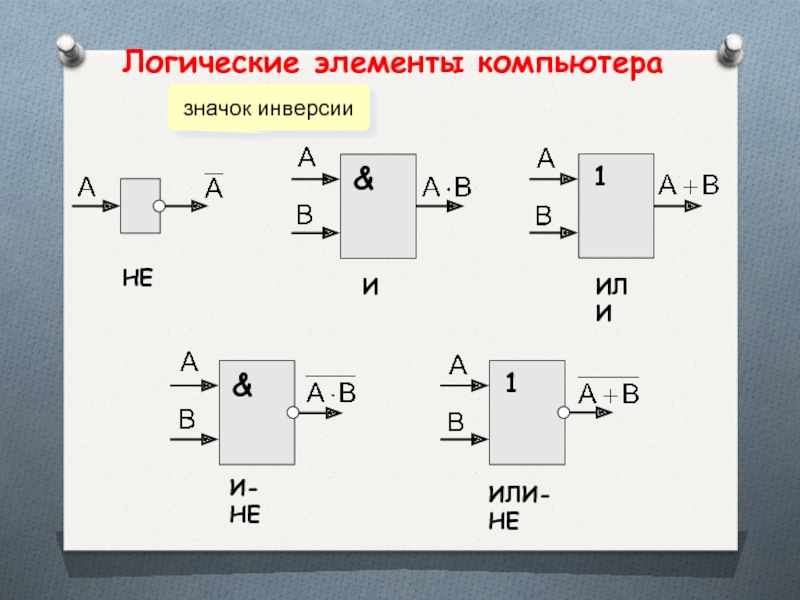
- 51. Логические элементы компьютераНЕИИЛИИЛИ-НЕИ-НЕзначок инверсии
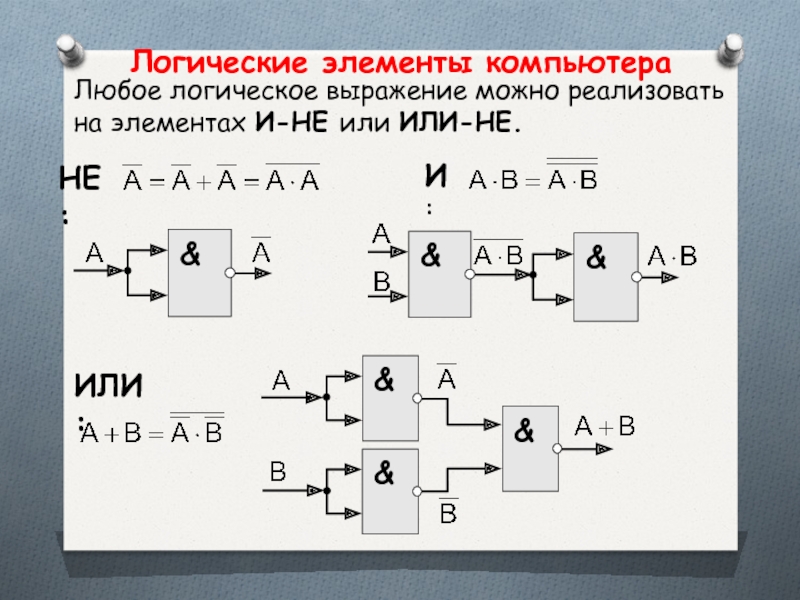
- 52. Логические элементы компьютераЛюбое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ.И:НЕ:ИЛИ:
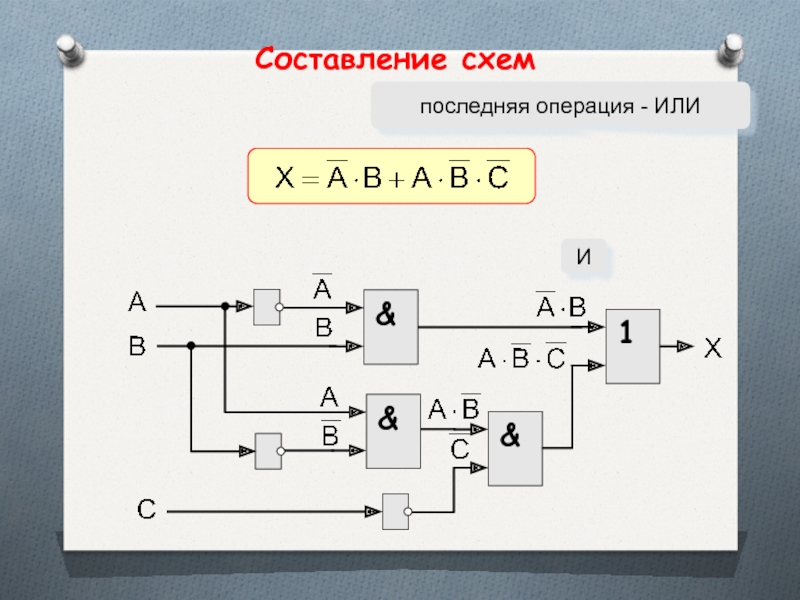
- 53. Составление схемпоследняя операция - ИЛИ&И
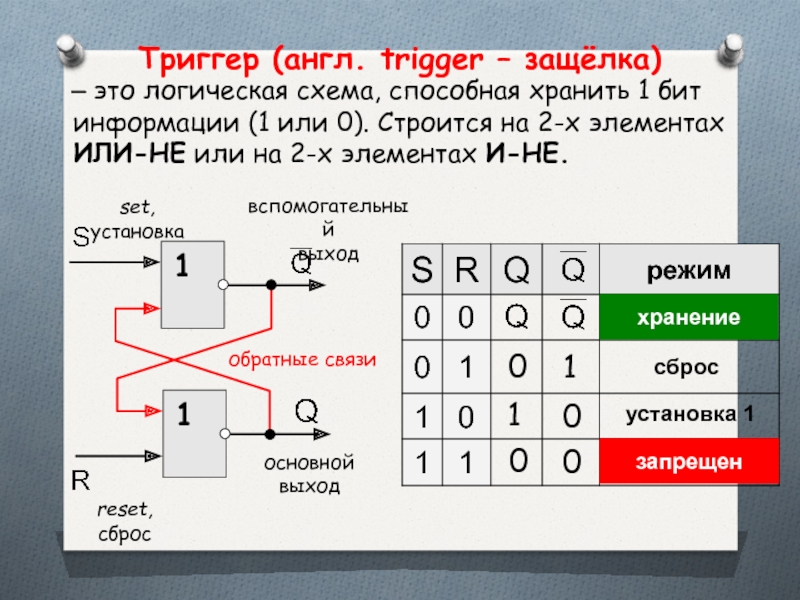
- 54. Триггер (англ. trigger – защёлка) –
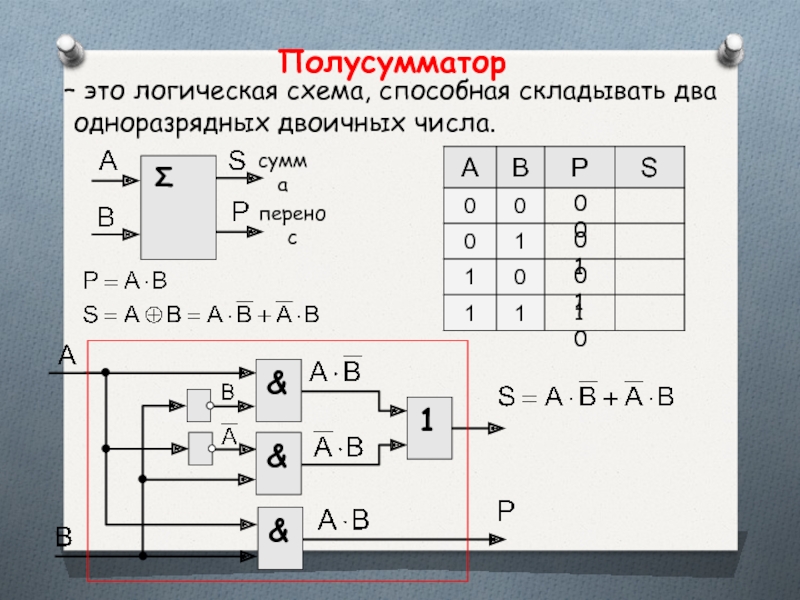
- 55. Полусумматор – это логическая схема, способная
- 56. Сумматор - это логическая схема, способная
Логика – это наука о формах и законах человеческого мышления.
Слайд 3Логика
Джордж Буль (1815-1864). Создал новую область науки - Алгебру логики (Булеву
алгебру или Алгебру высказываний).
Вильгельм Лейбниц (1646-1716). Основоположник математической логики (пытался построить первые логические исчисления: арифметические и буквенно-алгебраические).
Слайд 4Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, и
логические операции над ними.
Цель алгебры логики - описание поведения и структуры логических схем.
Объекты алгебры логики – высказывания.
Цель алгебры логики - описание поведения и структуры логических схем.
Объекты алгебры логики – высказывания.
Слайд 6Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать,
истинно оно или ложно.
Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
Слайд 8Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических связок (и; или; не; если, то; и др).
Слайд 9Так, например, из элементарных высказываний "Петров — врач", "Петров — шахматист"
при помощи связки "и" можно получить составное высказывание
"Петров — врач и шахматист", понимаемое как "Петров — врач, хорошо играющий в шахматы".
Слайд 10При помощи связки "или" из этих же высказываний можно получить составное
высказывание
"Петров — врач или шахматист",
понимаемое в алгебре логики как
"Петров или врач, или шахматист, или и врач и шахматист одновременно".
"Петров — врач или шахматист",
понимаемое в алгебре логики как
"Петров или врач, или шахматист, или и врач и шахматист одновременно".
Слайд 11В алгебре логики высказывания обозначают ЗАГЛАВНЫМИ буквами латинского алфавита и называют
логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
Слайд 12Так, например, предложение
" Трава зеленая" следует считать высказыванием, так как
оно истинное.
Записывается: А=1
Предложение " Лев - птица" тоже высказывание, так как оно ложное.
Записывается: В=0
Записывается: А=1
Предложение " Лев - птица" тоже высказывание, так как оно ложное.
Записывается: В=0
Слайд 13Пусть через А обозначено высказывание "Тимур поедет летом на море", а
через В — высказывание "Тимур летом отправится в горы".
Слайд 14Тогда составное высказывание "Тимур летом побывает и на море, и
в горах" можно кратко записать как
А и В
Здесь "и" — логическая связка, А, В — логические переменные, которые могут принимать только два значения - "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
А и В
Здесь "и" — логическая связка, А, В — логические переменные, которые могут принимать только два значения - "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Слайд 15A – Сейчас идет дождь.
B – Форточка открыта.
A и B
A или не B
если A, то B
не A и B
A тогда и только
тогда, когда B
A или не B
если A, то B
не A и B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Сейчас нет дождя и форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
Составьте из простых высказываний составные при помощи связок:
Слайд 17Операция НЕ
Операция, выражаемая словом "не", называется инверсией или
отрицанием и обозначается чертой над высказыванием.
Если высказывание A истинно,
то "не А" ложно, и наоборот.
Слайд 18Высказывание А истинно, когда A ложно, и ложно, когда A истинно.
Пример. "Луна — спутник Земли" (А);
"Луна — не спутник Земли" (А).
Слайд 191
0
0
1
таблица истинности операции НЕ
Таблица истинности
логического выражения F – это таблица,
где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения F для каждой комбинации.
Слайд 20Операция И
Операция, выражаемая связкой "и", называется конъюнкцией
(лат. conjunctio
— соединение)
или логическим умножением
и обозначается точкой " . "
(может также обозначаться знаками ^ или &).
или логическим умножением
и обозначается точкой " . "
(может также обозначаться знаками ^ или &).
Слайд 21Высказывание А · В истинно тогда и только тогда, когда оба
высказывания А и В истинны.
Например, высказывание
"10 делится на 2 и 5 больше 3" истинно, а высказывания:
"10 делится на 2 и 5 не больше 3",
"10 не делится на 2 и 5 больше 3",
"10 не делится на 2 и 5 не больше 3" — ложны.
Например, высказывание
"10 делится на 2 и 5 больше 3" истинно, а высказывания:
"10 делится на 2 и 5 не больше 3",
"10 не делится на 2 и 5 больше 3",
"10 не делится на 2 и 5 не больше 3" — ложны.
Слайд 23Операция ИЛИ
Операция, выражаемая связкой "или" называется дизъюнкцией
(лат. disjunctio
— разделение)
или логическим сложением и обозначается знаком v (или + «плюсом»).
или логическим сложением и обозначается знаком v (или + «плюсом»).
Слайд 24Высказывание А v В ложно тогда и только тогда, когда оба
высказывания А и В ложны.
Например, высказывание
"10 не делится на 2 или 5 не больше 3" ложно, а высказывания
"10 делится на 2 или 5 больше 3",
"10 делится на 2 или 5 не больше 3",
"10 не делится на 2 или 5 больше 3"— истинны.
Например, высказывание
"10 не делится на 2 или 5 не больше 3" ложно, а высказывания
"10 делится на 2 или 5 больше 3",
"10 делится на 2 или 5 не больше 3",
"10 не делится на 2 или 5 больше 3"— истинны.
Слайд 26Базовый набор операций
С помощью операций И, ИЛИ и НЕ можно реализовать
любую логическую операцию.
Слайд 27Операция ЕСЛИ-ТО
Операция, выражаемая связками "если ..., то", "из
... следует", "... влечет ...",
называется импликацией
(лат. implico — тесно связаны) и обозначается знаком . Высказывание А В ложно тогда и только тогда, когда А истинно, а В ложно.
называется импликацией
(лат. implico — тесно связаны) и обозначается знаком . Высказывание А В ложно тогда и только тогда, когда А истинно, а В ложно.
Слайд 28
A – "Работник хорошо работает".
B – "У работника хорошая
зарплата".
1
1
1
0
Таблица истинности импликации
Слайд 29Операция РАВНОСИЛЬНО
Операция, выражаемая связками "тогда и только тогда", "необходимо
и достаточно", "... равносильно ...", называется эквиваленцией и обозначается знаком или ~.
Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.
Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.
Слайд 31С помощью логических переменных и символов логических операций любое высказывание можно
формализовать, то есть заменить логической формулой.
Слайд 32Определение логической формулы:
1. Всякая логическая переменная и символы "истина" ("1")
и "ложь" ("0") - формулы.
2. Если А и В - формулы, то А , А · В ,
А v В , А B , А В - формулы.
3. Никаких других формул в алгебре логики нет.
2. Если А и В - формулы, то А , А · В ,
А v В , А B , А В - формулы.
3. Никаких других формул в алгебре логики нет.
Слайд 33Порядок выполнения логических операций в сложном логическом выражении
1.Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5.
Эквивалентность.
Слайд 34Определите истинность составного высказывания:
(А&В) & (C\/D), состоящего из простых высказываний:
А = {Принтер – устройство вывода информации},
В = {Процессор – устройство хранения информации},
С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.
Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний:
А = 1, В = 0, С = 1, D = 0.
Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:
( 1 & 0 ) &(1 \/ 0) = (0 & 1) & (1 \/ 0) = 0
Составное высказывание ложно.
Слайд 35
Даны простые высказывания:
А = {Принтер – устройство ввода информации},
В =
{Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
Определите истинность составных высказываний:
а) (А & В) & (C v D);
б) (А & В) => (C v D);
в) (А v В) ⬄ (C & D);
г) А ⬄ B .
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.
Определите истинность составных высказываний:
а) (А & В) & (C v D);
б) (А & В) => (C v D);
в) (А v В) ⬄ (C & D);
г) А ⬄ B .
Слайд 36Логические выражения и их таблицы истинности
Составные высказывания в алгебре логики записываются
с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.
логическая формула
Слайд 37Таблица истинности - это табличное представление логической схемы (операции), в котором
перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
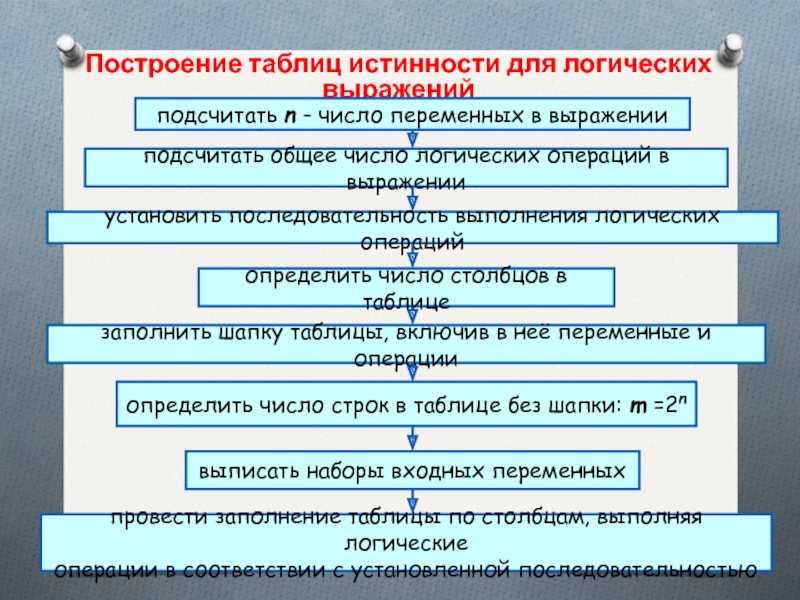
Слайд 38Построение таблиц истинности для логических выражений
подсчитать n - число переменных в
выражении
подсчитать общее число логических операций в выражении
установить последовательность выполнения логических операций
определить число столбцов в таблице
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2n
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью
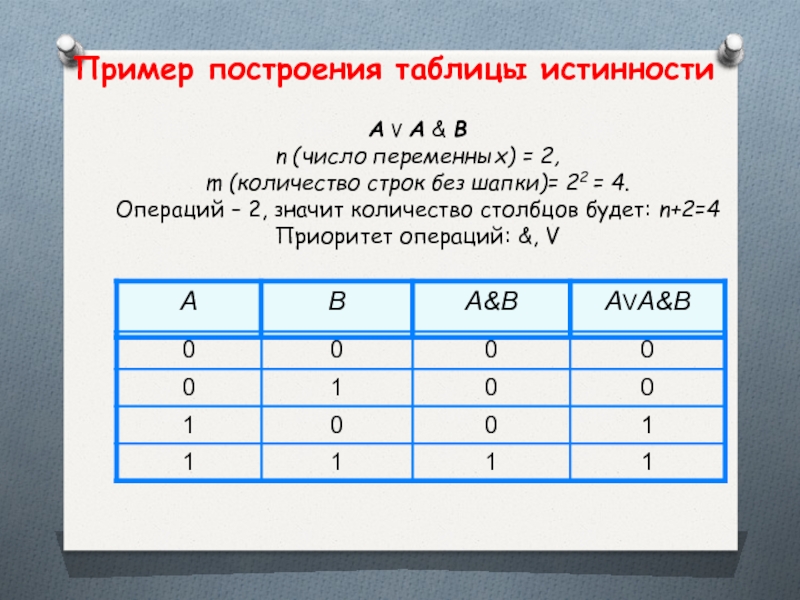
Слайд 39А V A & B
n (число переменных) = 2,
m (количество
строк без шапки)= 22 = 4.
Операций – 2, значит количество столбцов будет: n+2=4
Приоритет операций: &, V
Операций – 2, значит количество столбцов будет: n+2=4
Приоритет операций: &, V
Пример построения таблицы истинности
Слайд 43Закон тождества
A = A
Закон тождества означает, что в процессе рассуждения нельзя
подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.
Например, рассуждение Правильно говорят, что язык до Киева доведет, а я купил вчера копченый язык, значит, теперь смело могу идти в Киев неверно, так как первое и второе слова «язык» обозначают разные понятия.
Например, рассуждение Правильно говорят, что язык до Киева доведет, а я купил вчера копченый язык, значит, теперь смело могу идти в Киев неверно, так как первое и второе слова «язык» обозначают разные понятия.
Всякое понятие и суждение тождественно самому себе.
Слайд 44Закон непротиворечия
A & notA = 0
Не могут быть одновременно истинны утверждение
и его отрицание.
То есть если высказывание А— истинно, то его отрицание не А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным.
Это равенство часто используется при упрощении сложных логических выражений.
Примеры невыполнения закона непротиворечия:
1. На Марсе есть жизнь и на Марсе жизни нет.
2. Оля окончила среднюю школу и учится в X классе.
Слайд 45Закон исключения третьего
A and not A = 1
В один и тот
же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано.
Истинно либо А, либо не А.
Примеры выполнения закона исключенного третьего:
1. Число 12345 либо четное, либо нечетное, третьего не дано.
2. Предприятие работает убыточно или безубыточно.
3. Эта жидкость является или не является кислотой.
Слайд 46Закон двойного отрицания
Not (notA)=1
Если отрицать дважды некоторое высказывание, то в результате
получается исходное высказывание.
Например, высказывание
А = Матроскин — кот эквивалентно высказыванию
А = Неверно, что Матроскин не кот.
Например, высказывание
А = Матроскин — кот эквивалентно высказыванию
А = Неверно, что Матроскин не кот.
Слайд 48Логический элемент компьютера — это часть электронной логической схемы, которая реализует
элементарную логическую функцию.
Слайд 49Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ
и другие.
Слайд 50Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую
функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Слайд 52Логические элементы компьютера
Любое логическое выражение можно реализовать на элементах И-НЕ или
ИЛИ-НЕ.
И:
НЕ:
ИЛИ:
Слайд 54Триггер (англ. trigger – защёлка)
– это логическая схема, способная
хранить 1 бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
основной
выход
вспомогательный
выход
reset, сброс
set, установка
обратные связи
1
1
0
0
0
0
Слайд 55Полусумматор
– это логическая схема, способная складывать два одноразрядных двоичных
числа.
0 0
0 1
0 1
1 0
Слайд 56Сумматор
- это логическая схема, способная складывать два одноразрядных двоичных
числа с переносом из предыдущего разряда.
Σ
сумма
перенос
перенос
