- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему
Содержание
- 1. Презентация по информатике на тему
- 2. (от греческого logos – слово, понятие, рассуждение,
- 3. Первые учения о формах и способах рассуждений
- 4. Логическое высказывание – это любое повествовательное предложение,
- 5. Не всякое предложение является высказыванием. Например, предложение
- 6. ВЫСКАЗЫВАНИЯЭлементарные (простые)А = «Аристотель основоположник логики» =
- 7. Истинность и ложность составных высказываний зависит от
- 8. Основные операции алгебры высказыванийКаждая логическая связка
- 9. Логическое отрицаниеинверсия – это операция выраженная связкой
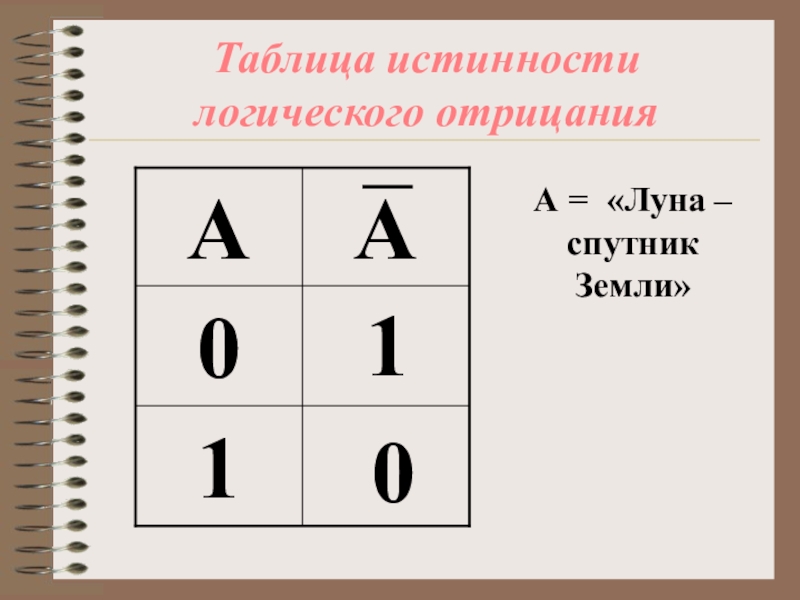
- 10. Таблица истинности логического отрицанияА = «Луна – спутник Земли»10
- 11. Логическое умножениеконъюнкция – это операция выраженная связкой
- 12. Таблица истинности логического умножения100010 не : 2
- 13. Логическое сложениедизъюнкция – это операция выраженная связкой
- 14. Таблица истинности логического сложения101110 не : 2
- 15. Операция импликация– это операция выраженная связкой «ЕСЛИ
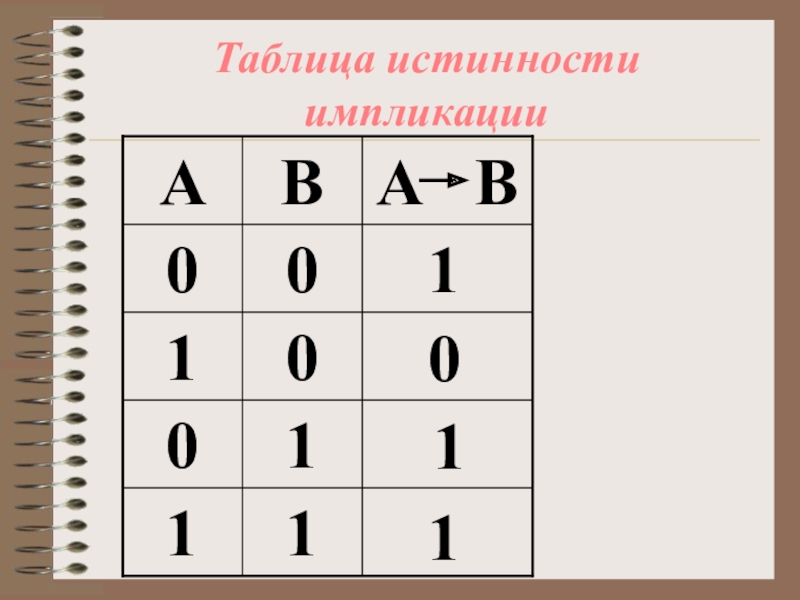
- 16. Таблица истинности импликации1101
- 17. Пример: Каким же образом импликация связывает два
- 18. Операция эквиваленция– это операция выраженная связкой
- 19. Таблица истинности эквиваленции110024 не : 6 ~
- 20. Приоритет операцийДействия в скобкахИнверсияКонъюнкцияДизъюнкцияИмпликацияЭквиваленция
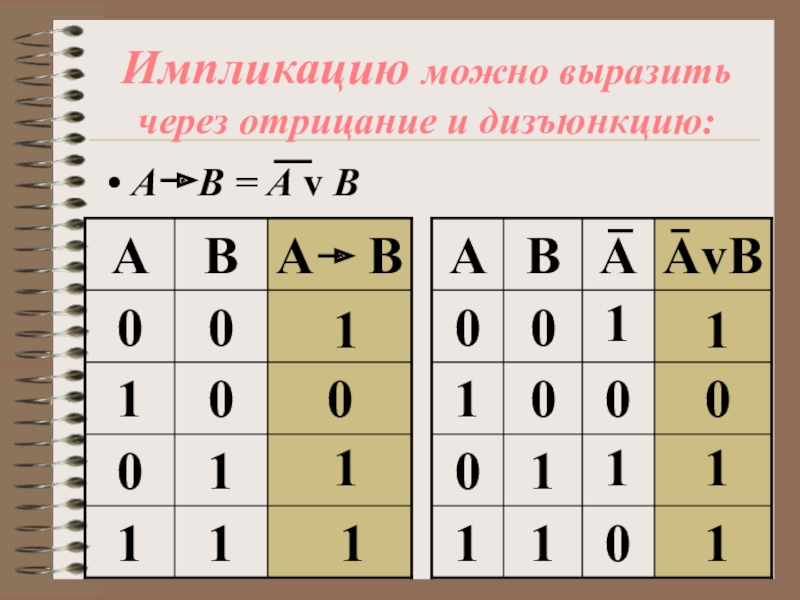
- 21. Импликацию можно выразить через отрицание и дизъюнкцию:А В = А v В000011111111
- 22. Эквиваленцию можно выразить через отрицание, дизъюнкцию и
- 23. Высказывания, у которых таблицы истинности совпадают, называются
- 24. Логическая формулаС помощью логических переменных и символов
- 25. Тождественно – истинные формулы
- 26. Тождественно – ложные формулы
- 27. Указанные операции хорошо иллюстрируются с помощью диаграмм Эйлера - Вейна.ААВотрицаниеконъюнкцияАВдизъюнкцияА ^ ВА v В
- 28. Определите с помощью таблиц истинности, какие из
Слайд 2(от греческого logos – слово, понятие, рассуждение, разум) или: формальная логика,
это раздел математической логики, изучающий строение сложных логических высказываний и способ установления их истинности с помощью алгебраических методов
ЛОГИКА
Слайд 3Первые учения о формах и способах рассуждений возникли в странах Древнего
XIX век – алгебра высказываний. Основатель алгебры логики – математик Джордж Буль.
ЛОГИКА
Слайд 4Логическое высказывание – это любое повествовательное предложение, в отношении которого можно
В алгебре высказываний суждениям (высказываниям) ставятся в соответствие логические переменные (заглавные буквы латинского алфавита)
А = 2 х 2 = 4=1 (истинно)
В = 2 х 2 =10 = 0 (ложно)
Слайд 5Не всякое предложение является высказыванием. Например, предложение «Ученик 11 класса» -
Вопросительные и восклицательные предложения также не являются высказываниями, так как говорить о их истинности или ложности не смысла.
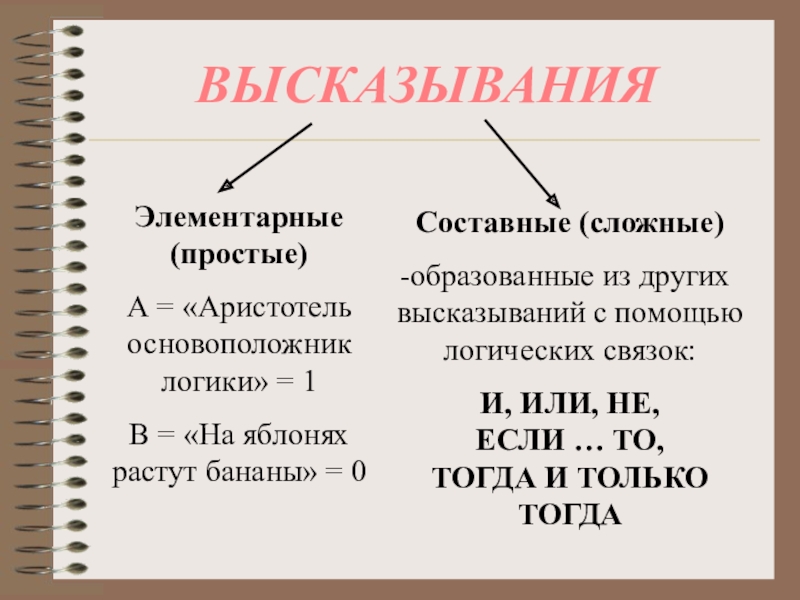
Слайд 6ВЫСКАЗЫВАНИЯ
Элементарные (простые)
А = «Аристотель основоположник логики» = 1
В = «На яблонях
Составные (сложные)
образованные из других высказываний с помощью логических связок:
И, ИЛИ, НЕ,
ЕСЛИ … ТО,
ТОГДА И ТОЛЬКО ТОГДА
Слайд 7Истинность и ложность составных высказываний зависит от истинности или ложности элементарных
Так, А = 1, В = 0, то А и В = 0
Слайд 8Основные операции
алгебры высказываний
Каждая логическая связка рассматривается как операция над логическими
Слайд 9Логическое отрицание
инверсия – это операция выраженная связкой «НЕ»
с латинского – inversio
А (А, not)
Высказывание А истинно, когда А – ложно , и ложно, когда А - истинно
Таблица истинности – таблица, которая показывает какие значения принимает составное высказывание при всех наборах значений, входящих в него простых высказываний.
Слайд 11Логическое умножение
конъюнкция – это операция выраженная связкой «И»
с латинского – conjunctio
А^B (&, *, and)
Высказывание А^B истинно, тогда и только тогда, когда оба высказывания истинны
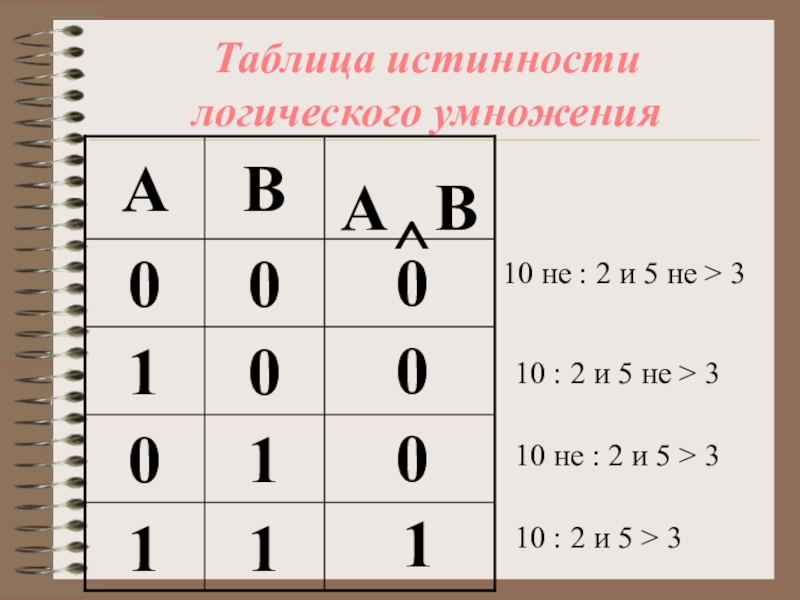
Слайд 12Таблица истинности логического умножения
1
0
0
0
10 не : 2 и 5 не >
10 : 2 и 5 не > 3
10 не : 2 и 5 > 3
10 : 2 и 5 > 3
Слайд 13Логическое сложение
дизъюнкция – это операция выраженная связкой «ИЛИ»
с латинского – dizjunctio
АVB (+, or)
Высказывание АvB ложно, тогда и только тогда, когда оба высказывания ложны
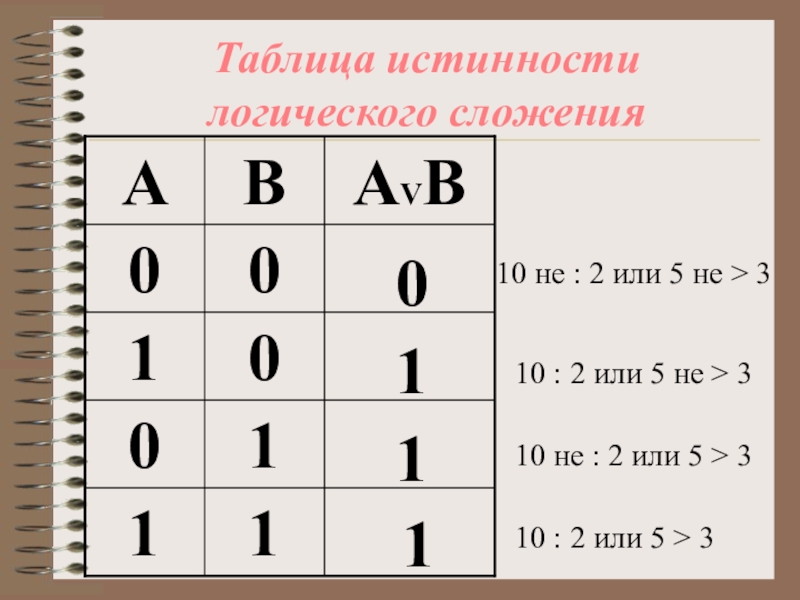
Слайд 14Таблица истинности логического сложения
1
0
1
1
10 не : 2 или 5 не >
10 : 2 или 5 не > 3
10 не : 2 или 5 > 3
10 : 2 или 5 > 3
Слайд 15Операция импликация
– это операция выраженная связкой «ЕСЛИ … ТО»
с латинского –
А B ( , логическое следование)
Высказывание А B ложно, тогда и только тогда, когда А - истинно, В – ложно (А = 1, В = 0)
Слайд 17Пример: Каким же образом импликация связывает два элементарных высказывания?
Даны два элементарных
Рассмотрим составное высказывание А-> В, понимаемое как «если данный четырехугольник квадрат, то около него можно описать окружность».
Есть три варианта, когда высказывание истинно:
1. А=1, В=1- «Данный четырехугольник квадрат и около него можно описать окружность»
2. А-0, В=1 - «Данный четырехугольник не является квадратом, но около него можно описать окружность»
3. А=0, В=0 - «Данный четырехугольник не является квадратом, и около него нельзя описать окружность»
Ложен только один вариант: А=1, В=0 - «Данный четырехугольник является квадратом, но около него нельзя описать окружность»
Слайд 18Операция эквиваленция
– это операция выраженная связкой
«ТОГДА И ТОЛЬКО ТОГДА»
с латинского
А ~ B ( , равнозначность)
Высказывание А ~ B истинно, тогда и только тогда, когда значения А и В совпадают
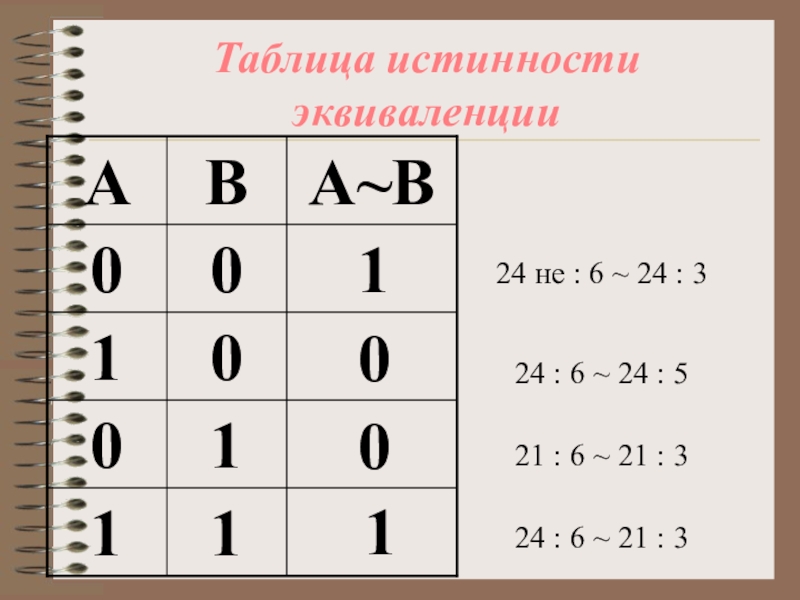
Слайд 19Таблица истинности эквиваленции
1
1
0
0
24 не : 6 ~ 24 : 3
24 :
21 : 6 ~ 21 : 3
24 : 6 ~ 21 : 3
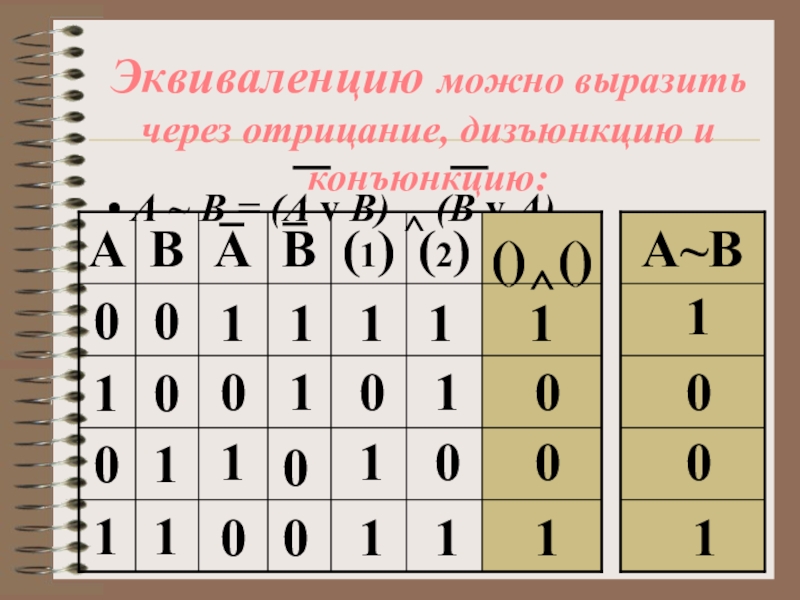
Слайд 22Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А ~ В =
0
0
0
0
1
1
1
1
1
1
1
0
1
0
1
1
0
0
1
1
0
0
1
1
Слайд 23Высказывания, у которых таблицы истинности совпадают, называются равносильными и обозначаются =
Пусть
Докажите, что: а) А ^ В = А v В б) А ~ В = (А ^ В) v (А ^ В)
Слайд 24Логическая формула
С помощью логических переменных и символов любое высказывание можно формализовать,
Определение логической формулы: 1. Всякая логическая переменная и символы «истина» и «ложь» - формулы. 2. Если А и В формулы, то А, А ^ В, А v В, А В, А ~ В формулы!
Слайд 25Тождественно – истинные формулы
Формулы, которые принимают
Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
А v А = «этот треугольник прямоугольный или косоугольный» = 1 и тогда, когда треугольник прямоугольный и тогда, когда треугольник непрямоугольный.
Слайд 26Тождественно – ложные формулы
Формулы, которые принимают
Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
А ^ А = «Катя – самая высокая девочка в классе и в классе есть девочки выше Кати» = 0 очевидно, что А или А – ложно.
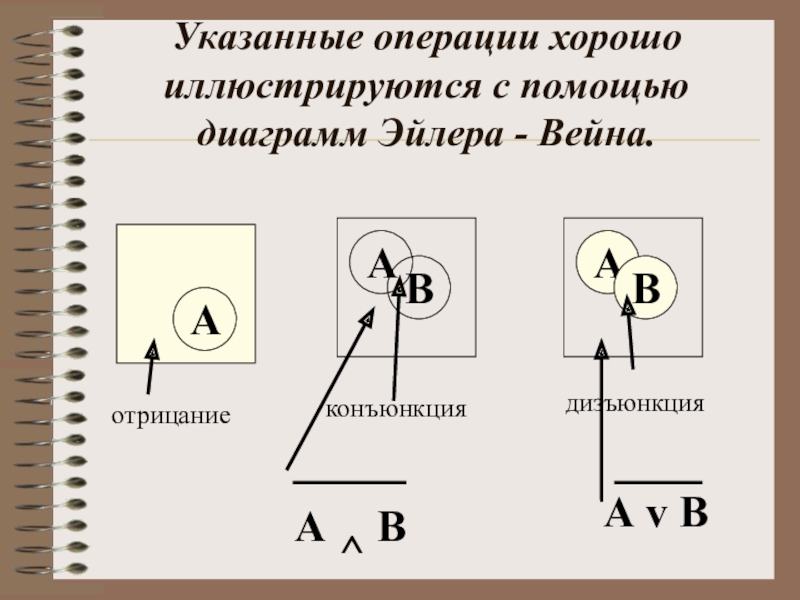
Слайд 27Указанные операции хорошо иллюстрируются с помощью диаграмм Эйлера - Вейна.
А
А
В
отрицание
конъюнкция
А
В
дизъюнкция
А ^
А v В
Слайд 28Определите с помощью таблиц истинности, какие из следующих формул являются тождественно
((А v В) В) ^ (А v В)
А ^ (В ^ (А v В))
((С v В) В) ^ ( А ^ В) В