- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Модели статистического прогнозирования (11 класс, учебник Семакина И.Г. и др)
Содержание
- 1. Презентация по информатике Модели статистического прогнозирования (11 класс, учебник Семакина И.Г. и др)
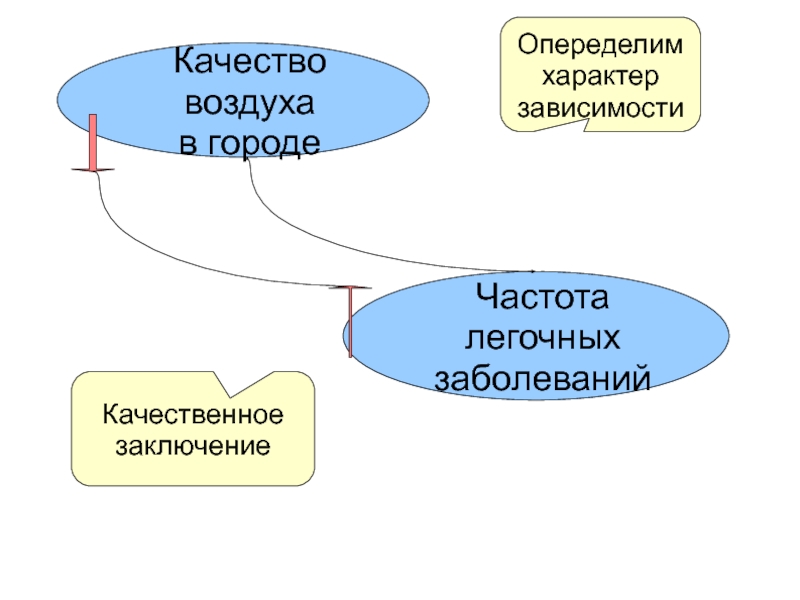
- 2. Качество воздуха в городеЧастота легочных заболеванийОпеределим характер зависимостиКачественное заключение
- 3. Уточнение характера зависимостиПримеси в воздухе, влияющие на
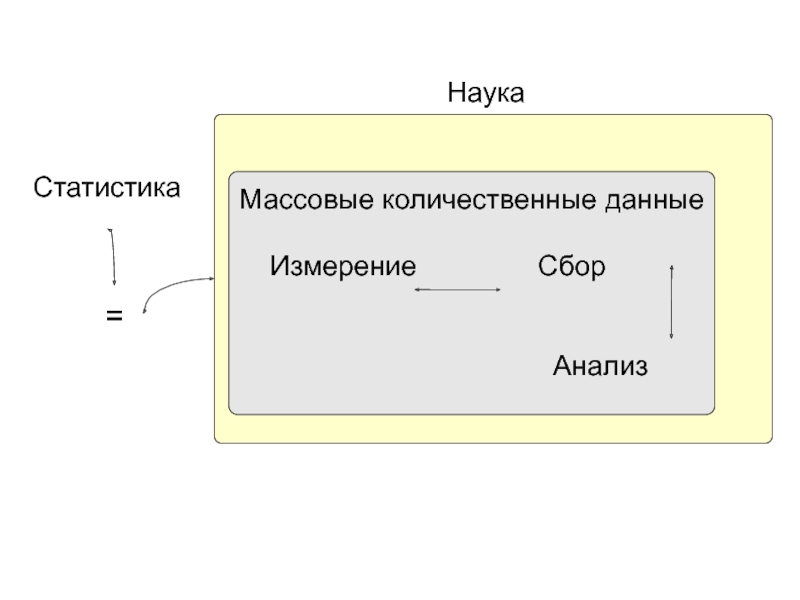
- 4. Массовые количественные данныеСтатистика=НаукаСборАнализИзмерение
- 5. СтатистикаЭкономическаяМедицинскаяСоциальнаяМатематическая статистика
- 6. Статистические данныеПриближённые, усреднённыеХарактер зависимости величиныВерно отражаютНосят оценочный
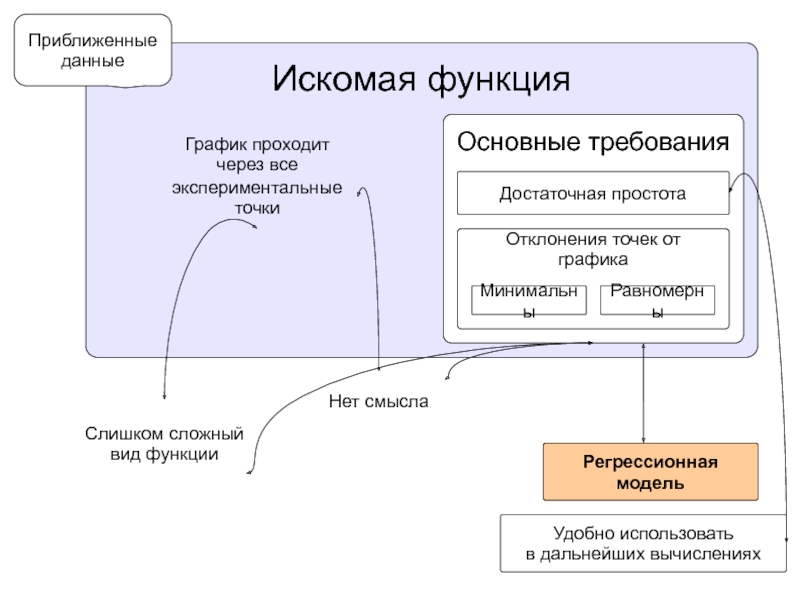
- 7. Искомая функцияГрафик проходит через все Слишком сложный
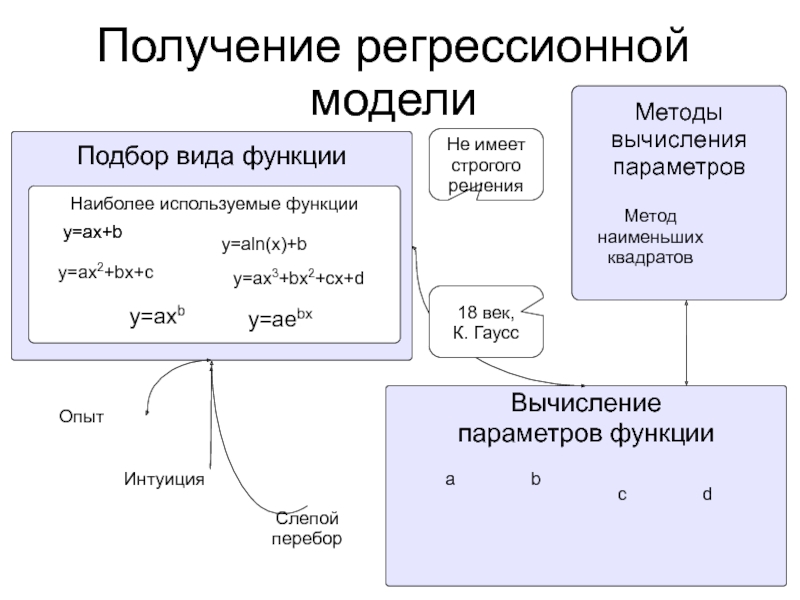
- 8. Получение регрессионной моделиПодбор вида функцииВычисление параметров функцииНе
- 9. Искомая функцияМНК(y1э-y1ф)2(y2э-y2ф)2(yiэ-yiф)2Σ (yiЭ-yiф)211i=1kminИскомая функция должна быть построена
- 10. Статистическая обработка данныхИспользуемые математические пакеты программМНКПостроение любой функцииКритерии соответствияРегрессионная модельГрафикТренд
- 11. Регрессионная модельФункцияГрафикФормулаКоэффициент детерминированностиИнтервал0 ... 1Удачная регрессионная модельR2Неудачная регрессионная модель
- 12. Регрессионная математическая модельЗначения, полученные путём измеренийПрогнозирование
Качество воздуха в городеЧастота легочных заболеванийОпеределим характер зависимостиКачественное заключение
Слайд 1Модели статистического прогнозирования
Презентация учителя информатики МБОУ БСОШ №6 г. Королёв
Тузова А.А.
Слайд 2Качество воздуха
в городе
Частота легочных
заболеваний
Опеределим
характер
зависимости
Качественное
заключение
Слайд 3Уточнение характера зависимости
Примеси в воздухе,
влияющие на
здоровье
Сильно влияющие
Несильно влияющие
Число заболеваний
Сбор
экспериментальных
данных
Анализ
Обобщение
Оксид
углерода
Должно
быть
много
Слайд 6Статистические данные
Приближённые,
усреднённые
Характер зависимости
величины
Верно
отражают
Носят оценочный характер
Оценочная
модель
Математическая модель
P=f(C)
Формульное выражение функциональной зависимости
График должен
проходить близко
к экспер. точкам
подбор
Матем. методы
Слайд 7Искомая функция
График проходит
через все
Слишком сложный
вид функции
экспериментальные
точки
Приближенные
данные
Нет смысла
Основные требования
Достаточная простота
Удобно использовать
в дальнейших
вычислениях
Отклонения точек от
графика
Минимальны
Равномерны
Регрессионная
модель
Слайд 8Получение регрессионной модели
Подбор вида функции
Вычисление
параметров функции
Не имеет строгого
решения
Опыт
Интуиция
Слепой
перебор
Наиболее используемые функции
y=ax+b
y=ax+b
y=ax2+bx+c
y=aln(x)+b
y=aebx
y=axb
y=ax3+bx2+cx+d
a
b
c
d
Методы
вычисления
параметров
Метод
наименьших
квадратов
18 век,
К.
Гаусс
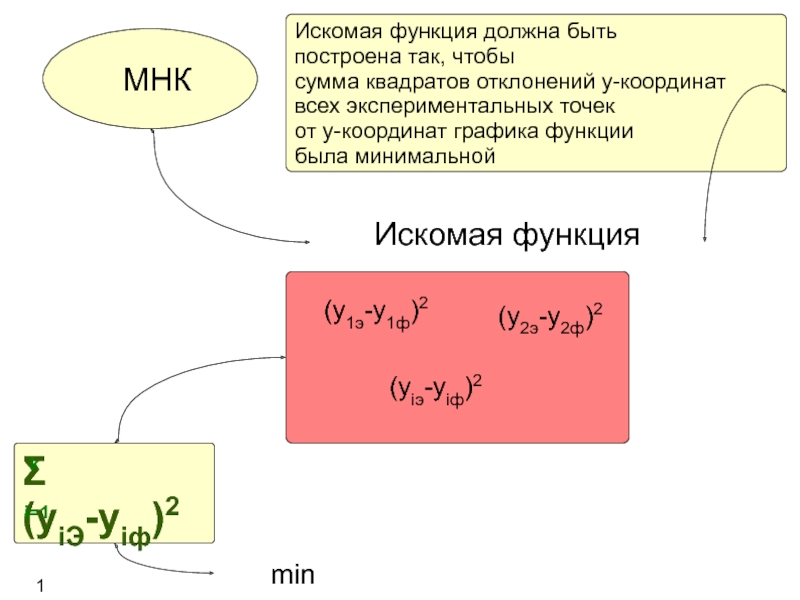
Слайд 9Искомая функция
МНК
(y1э-y1ф)2
(y2э-y2ф)2
(yiэ-yiф)2
Σ (yiЭ-yiф)2
11
i=1
k
min
Искомая функция должна быть
построена так, чтобы
сумма квадратов отклонений y-координат
всех
экспериментальных точек
от y-координат графика функции
была минимальной
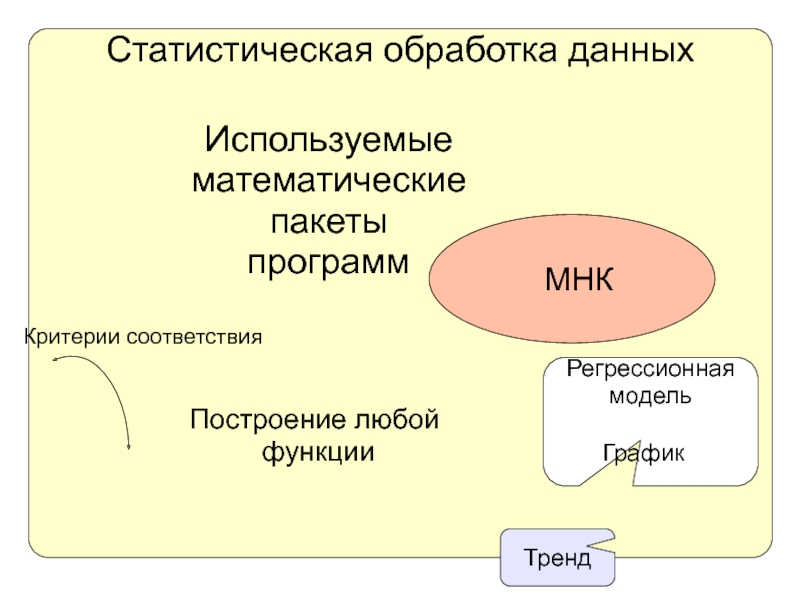
Слайд 10Статистическая обработка данных
Используемые
математические
пакеты
программ
МНК
Построение любой
функции
Критерии соответствия
Регрессионная
модель
График
Тренд
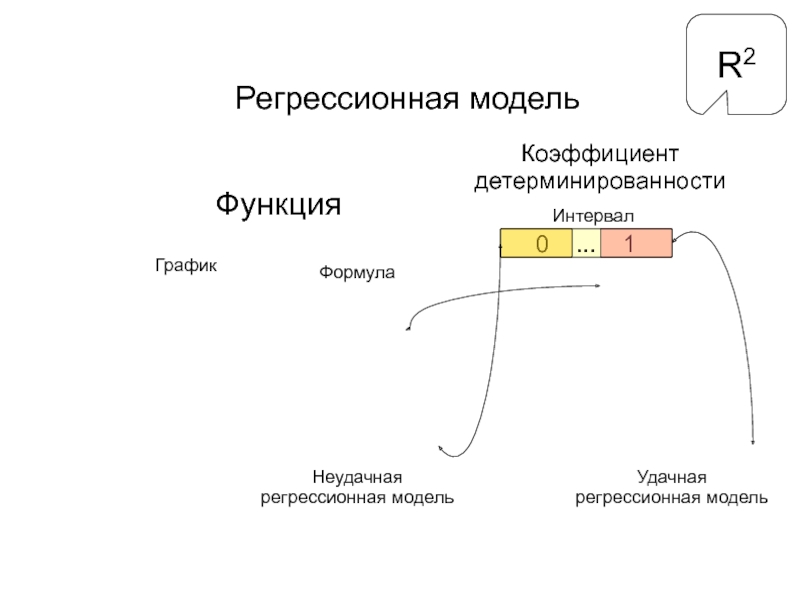
Слайд 11
Регрессионная модель
Функция
График
Формула
Коэффициент
детерминированности
Интервал
0 ... 1
Удачная
регрессионная модель
R2
Неудачная
регрессионная модель
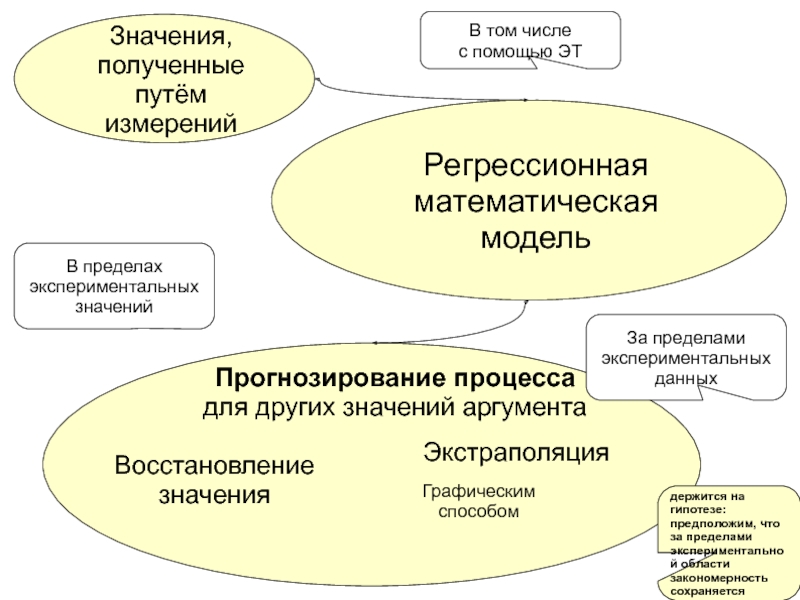
Слайд 12Регрессионная
математическая модель
Значения,
полученные путём
измерений
Прогнозирование процесса
для других значений аргумента
Восстановление
значения
Экстраполяция
В пределах
экспериментальных
значений
За пределами
экспериментальных
данных
В
том числе
с помощью ЭТ
Графическим
способом
держится на гипотезе: предположим, что за пределами экспериментальной области закономерность сохраняется