- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Логические операции (8 класс)
Содержание
- 1. Презентация по информатике Логические операции (8 класс)
- 2. Логическая операция – способ построения сложного высказывания
- 3. ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ)Инверсия образуется из высказывания с
- 4. ПРИМЕРЫ ОБРАЗОВАНИЯ ИНВЕРСИИ:
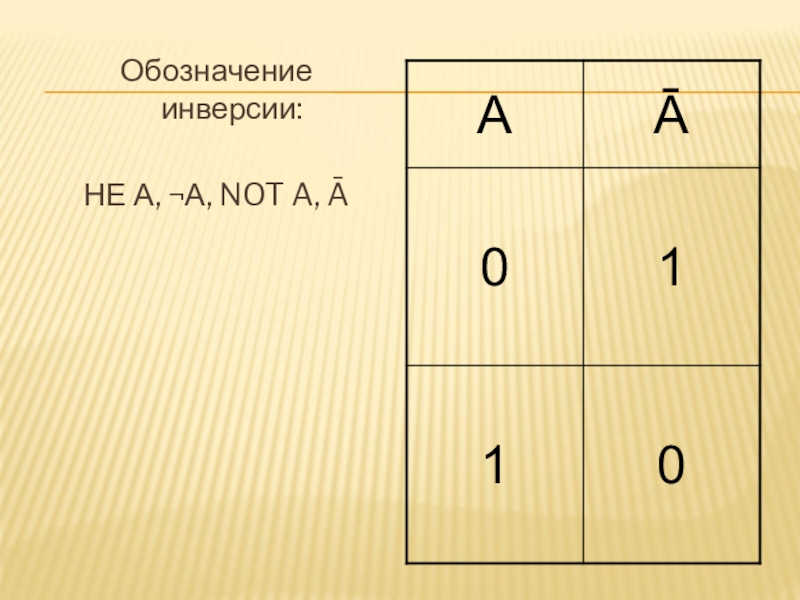
- 5. Обозначение инверсии:НЕ А, ¬А, NOT A, Ā
- 6. Из таблицы истинности следует, что инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно.
- 7. МНЕМОНИЧЕСКОЕ ПРАВИЛО:Слово «инверсия» (от лат. inversio –
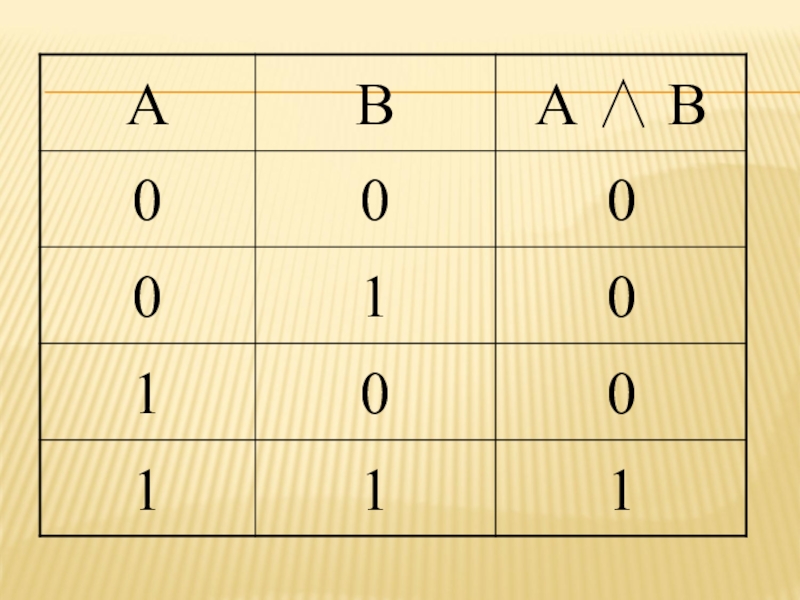
- 8. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ)Конъюнкция образуется соединением двух высказываний
- 9. ПРИМЕР:А = на автостоянке стоит «Мерседес»В =
- 10. Слайд 10
- 11. Из таблицы истинности следует, что конъюнкция двух
- 12. Слайд 12
- 13. МНЕМОНИЧЕСКОЕ ПРАВИЛО:Конъюнкция – это логическое умножение; равенства
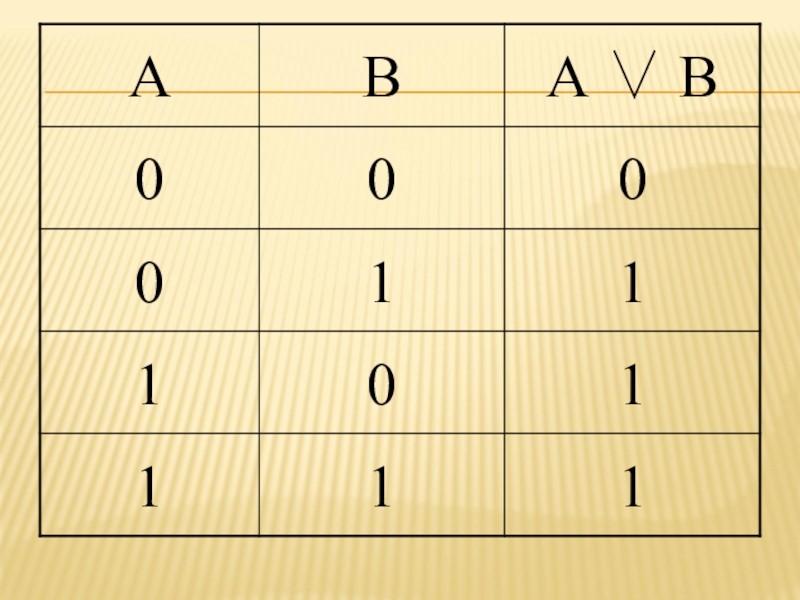
- 14. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)Дизъюнкция образуется соединением двух
- 15. Слайд 15
- 16. Из таблицы истинности следует, что дизъюнкция двух
- 17. Слайд 17
- 18. ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ)Импликация образуется соединением двух высказываний
- 19. Слайд 19
- 20. Из таблицы истинности следует, что импликация двух
- 21. Слайд 21
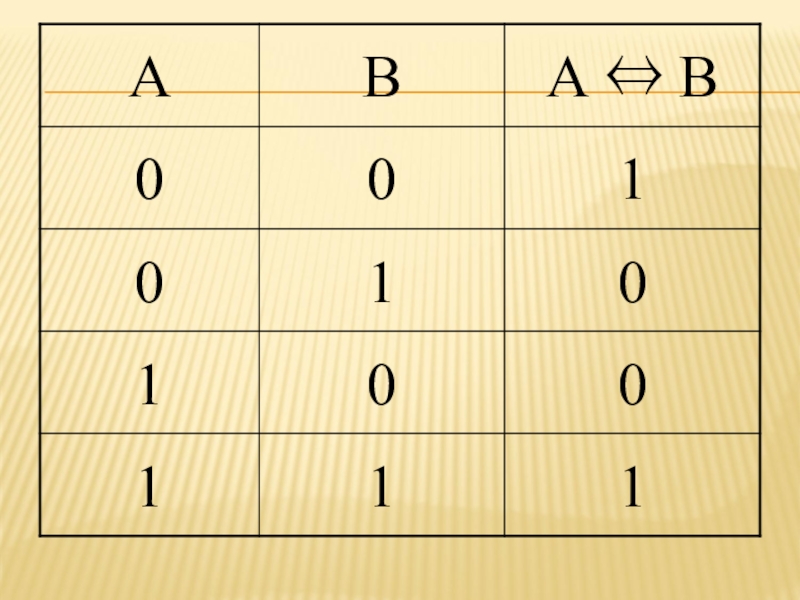
- 22. ЭКВИВАЛЕНТНОСТЬ (ЛОГИЧЕСКОЕ РАВЕНСТВО)Эквивалентность образуется соединением двух высказываний
- 23. Слайд 23
- 24. Из таблицы истинности следует, что эквивалентность двух
- 25. Слайд 25
Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Слайд 2Логическая операция – способ построения сложного высказывания из данных высказываний, при
котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Слайд 3ИНВЕРСИЯ
(ЛОГИЧЕСКОЕ ОТРИЦАНИЕ)
Инверсия образуется из высказывания с помощью добавления частицы «не» к
сказуемому или использования оборота речи «неверно, что…».
Слайд 6Из таблицы истинности следует, что инверсия высказывания истинна, когда высказывание ложно,
и ложна, когда высказывание истинно.
Слайд 7МНЕМОНИЧЕСКОЕ ПРАВИЛО:
Слово «инверсия» (от лат. inversio – переворачивание) означает, что белое
меняется на черное, добро на зло, красивое на безобразное, истина на ложь, ложь на истину, ноль на один, один на ноль.
Слайд 8КОНЪЮНКЦИЯ
(ЛОГИЧЕСКОЕ УМНОЖЕНИЕ)
Конъюнкция образуется соединением двух высказываний в одно с помощью союза
«и»
Обозначение конъюнкции:
А И В, А ∧ В, А & В, А AND В, А·В
Обозначение конъюнкции:
А И В, А ∧ В, А & В, А AND В, А·В
Слайд 9ПРИМЕР:
А = на автостоянке стоит «Мерседес»
В = на автостоянке стоят «Жигули»
(А
∧ В) = на автостоянке стоят «Мерседес» и «Жигули»
Слайд 11Из таблицы истинности следует, что конъюнкция двух высказываний истинна тогда и
только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.
Слайд 13МНЕМОНИЧЕСКОЕ ПРАВИЛО:
Конъюнкция – это логическое умножение; равенства 0·0=0, 0·1=0, 1·0=0, 1·1=1
верны для обычного умножения, верны и для конъюнкции.
Слайд 14ДИЗЪЮНКЦИЯ
(ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)
Дизъюнкция образуется соединением двух высказываний в одно с помощью
союза «или».
Обозначение дизъюнкции:
А ИЛИ В, А OR В, А | В, А ∨ В, А+В
Обозначение дизъюнкции:
А ИЛИ В, А OR В, А | В, А ∨ В, А+В
Слайд 16Из таблицы истинности следует, что дизъюнкция двух высказываний ложна тогда и
только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.
Слайд 18ИМПЛИКАЦИЯ
(ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ)
Импликация образуется соединением двух высказываний в одно с помощью оборота
речи «если…, то…»
Обозначение импликации:
А → В, А ⇒ В
Обозначение импликации:
А → В, А ⇒ В
Слайд 20Из таблицы истинности следует, что импликация двух высказываний ложна тогда и
только тогда, когда из истинного высказывания следует ложное.
Слайд 22ЭКВИВАЛЕНТНОСТЬ
(ЛОГИЧЕСКОЕ РАВЕНСТВО)
Эквивалентность образуется соединением двух высказываний в одно при помощи оборота
речи «… тогда и только тогда, когда …»
Обозначение эквивалентности:
А ≡ В, А ⇔ В, А ~ В
Обозначение эквивалентности:
А ≡ В, А ⇔ В, А ~ В
Слайд 24Из таблицы истинности следует, что эквивалентность двух высказываний истинна тогда и
только тогда, когда оба высказывания истинны или оба ложны.