Презентация, доклад по информатике кодирование числовой информации

Содержание

Двоичный кодВся информация, которую обрабатывает компьютер, должна быть представлена двоичным кодом с помощью двух цифр – 0 и 1.Эти два символа 0 и 1 принято называть битами (от англ. binary digit – двоичный знак).

Слайд 1Подготовлена преподавателем информатики: Ивановой Е.Г.
Кодирование числовой информации в компьютере

Подготовлена преподавателем информатики: Ивановой Е.Г.Кодирование числовой информации в компьютере

Слайд 2Двоичный код
Вся информация, которую обрабатывает компьютер, должна быть представлена двоичным кодом

с помощью двух цифр – 0 и 1.
Эти два символа 0 и 1 принято называть битами (от англ. binary digit – двоичный знак).
Двоичный кодВся информация, которую обрабатывает компьютер, должна быть представлена двоичным кодом с помощью двух цифр – 0

Слайд 3Кодирование и декодирование
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером,

т.е. двоичный код.

Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Кодирование и декодированиеКодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.Декодирование – преобразование данных

Слайд 4Способы кодирования
Способы кодирования и декодирования информации в компьютере, в первую очередь,

зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.
Способы кодированияСпособы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно,

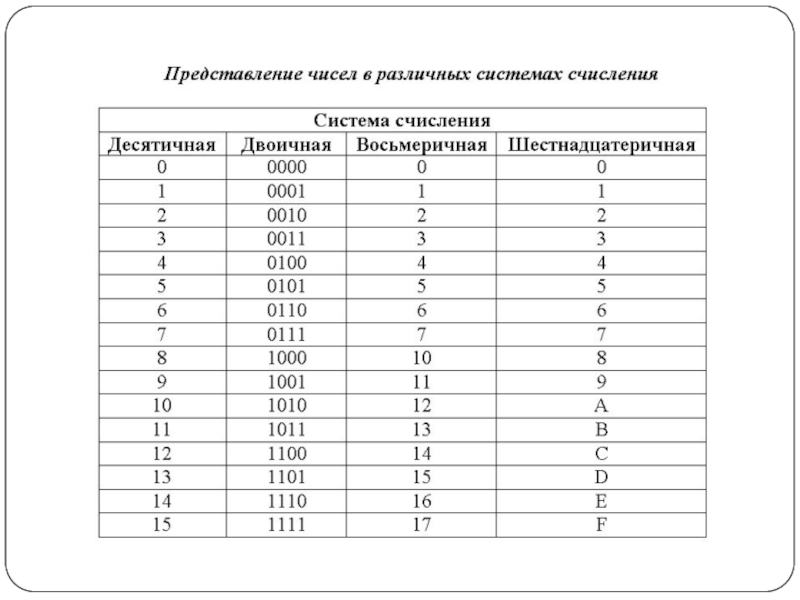
Слайд 5Представление чисел
Для записи информации о количестве объектов используются числа. Числа записываются

с использование особых знаковых систем, которые называют системами счисления.
Система счисления – совокупность приемов и правил записи чисел с помощью определенного набора символов.
Представление чиселДля записи информации о количестве объектов используются числа. Числа записываются с использование особых знаковых систем, которые

Слайд 6Позиционные и непозиционные системы счисления
Все системы счисления делятся на две большие

группы:

Количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
0,7 7 70

Количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
XIX

Позиционные и непозиционные системы счисленияВсе системы счисления делятся на две большие группы:Количественное значение каждой цифры числа зависит

Слайд 8Римская непозиционная система счисления
Самой распространенной из непозиционных систем счисления является римская.

В качестве цифр используются: I(1), V(5), X(10), L(50), C(100), D(500), M(1000).
Величина числа определяется как сумма или разность цифр в числе.
MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1 = 1998
Римская непозиционная система счисленияСамой распространенной из непозиционных систем счисления является римская. В качестве цифр используются: I(1), V(5),

Слайд 9Перевести числа в десятичную систему счисления

Перевести числа в десятичную систему счисления

Слайд 10Проверочный слайд I(1), V(5), X(10), L(50), C(100), D(500), M(1000).

Проверочный слайд I(1), V(5), X(10), L(50), C(100), D(500), M(1000).

Слайд 12Позиционные системы счисления
Первая позиционная система счисления была придумана еще в Древнем

Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр!
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления.
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
Позиционные системы счисленияПервая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная,

Слайд 14Основание системы счисления
Количество различных символов, используемых для изображения числа в позиционных

системах счисления, называется основанием системы счисления.
Основание системы счисленияКоличество различных символов, используемых для изображения числа в позиционных системах счисления, называется основанием системы счисления.

Слайд 15 13810 = 100010102
Перевод

из десятичной системы
Счисления в двоичную

11110 =

7910 =

самостоятельное задание

11011112

10011112

13810 = 100010102 Перевод из десятичной системы Счисления

Слайд 1611110

7910
11110 7910

Слайд 17Перевод из двоичной системы счисления в десятичную
3 2 1 0
6354 –

тысяч (разряд 4, 103 ) - 6
сотен (разряд 3, 102) – 3
десяток (разряд 2, 101) – 5
единиц (разряд 1, 100) – 4
6354= 6*103+3*102+5*101+4*100

20=1
21=2
22=4
23-8
24-16
25=32
26=64
27=128
28=256


7 6 5 4 3 2 1 0
10101001= 1*27+0*26+1*25+0*24+1*23+0*22+0*21+1*20 =
128+32+8+1=169

Перевод из двоичной системы счисления в десятичную3 2 1 06354 – тысяч (разряд 4, 103 ) -

Слайд 18Домашнее задание:
1. Перевести в римскую систему счисления:
2985
3485
2. Перевести из десятичной

системы счисления в двоичную числа: 39; 101; 256
3. Перевести из двоичной системы счисления в десятичную : 10101; 111000; 1000000;



MMMCMLXXXV
MMMCDLXXXV


((100111;1100101;100000000)


( (21;56;64)

Домашнее задание: 1. Перевести в римскую систему счисления: 2985 34852. Перевести из десятичной системы счисления в двоичную числа:

Слайд 201010101112  ?8 101.010.111 5.2.7 8

1010101112=527 8 10110011= ?8

111100002  ?8
10101012  ?8

111100002 = 3608

10101012  1258

Перевод чисел из двоичной системы счисления в восьмеричную с использованием таблицы

1010101112  ?8 101.010.111 5.2.7 8 1010101112=527 8

Слайд 21558  ?2

5.58 101.1012 558= 1011012 1128= ?2

1008  ?2
5558 ?2

1008 = 10000002

5438= 1011000112

Перевод чисел из восьмеричной системы счисления в двоичную с использованием таблицы

558  ?2 5.58 101.1012

Слайд 221010111112  ?16 1.0101.1111 1.5.F 16 1010111112=

15F16 10110011= ?16

111100002  ?16
10101012  ?16

111100002 = F08

10101012 =55 16

Перевод чисел из двоичной системы счисления в шестнадцатиричную

1010111112  ?16 1.0101.1111 1.5.F 16 1010111112= 15F16 10110011=

Слайд 235B16  ?2

5.B8 0101.10112 5B8= 1011011 2 1c28= ?2

1016  ?2
55516 ?2

1016 = 100002

5FC16= 101111111002

Перевод чисел из шестнадцатеричной системы счисления в двоичную с использованием таблицы

5B16  ?2 5.B8 0101.10112

Слайд 27Расположите числа, записанные в различных системах счисления, в порядке возрастания
1 вариант
3510,

368, 3А16, 1001012  

2 вариант

1110012, 648, 9Е16, 2510

Расположите числа, записанные в различных системах счисления, в порядке возрастания1 вариант3510, 368, 3А16, 1001012  2 вариант1110012, 648,

Слайд 28Проверочный слайд Расположите числа, записанные в различных системах счисления, в порядке возрастания
1

вариант
3510, 368, 3А16, 1001012,  
(Ответ: 368, 3510, 1001012, 3А16 )
2 вариант

1110012, 648, 9Е16, 2510,
(Ответ: 2510, 648, 1110012, 9Е16 )
Проверочный слайд Расположите числа, записанные в различных системах счисления, в порядке возрастания1 вариант3510, 368, 3А16, 1001012,  (Ответ:
Скачать презентацию

Похожие презентации

Зависимость Зависимость 204
Презентация по информатике История возникновения языка HTML Презентация по информатике История возникновения языка HTML 241
Мультимедиа Мультимедиа 155
Презентация к докладу Формирование УУД на уроках информатики в условиях внедрения ФГОС-II Презентация к докладу Формирование УУД на уроках информатики в условиях внедрения ФГОС-II 128
Презентация по теме Техника безопасности на уроках информатики Презентация по теме Техника безопасности на уроках информатики 225
Проект на тему: Компьютерные игры - хорошо или плохо? Проект на тему: Компьютерные игры - хорошо или плохо? 227

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть