- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике и ИКТ Системы счисления
Содержание
- 1. Презентация по информатике и ИКТ Системы счисления
- 2. Система счисления — это знаковая система, в
- 3. Классификация систем счисленияПозиционные: величина, обозначаемая цифрой,
- 4. Непозиционные системы счисленияАлфавит системы содержит неограниченное количество символов.
- 5. Славянская система счисления
- 6. Древнегреческая (ионийская) система счисления1 – I2 –
- 7. Римская система счисления1 – I 5 –
- 8. Римская система счисленияЗадание 1:Переведите числа из римской
- 9. Недостатки непозиционной системы счисления:Для записи больших чисел
- 10. Позиционные системы счисленияТроичная – 0, 1, 2Пятеричная
- 11. Десятичная система счисленияНачало десятичной системе счисления было
- 12. Позиционные системы счисленияОснование системы – это количество
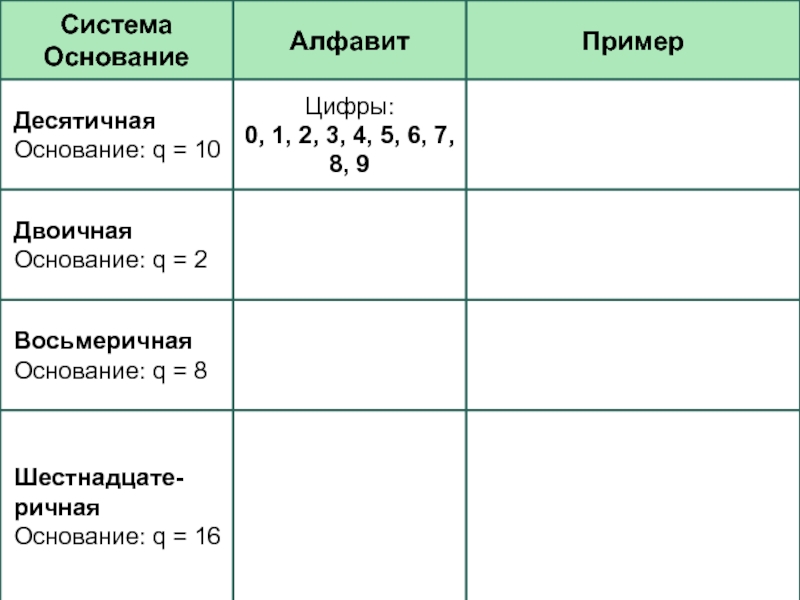
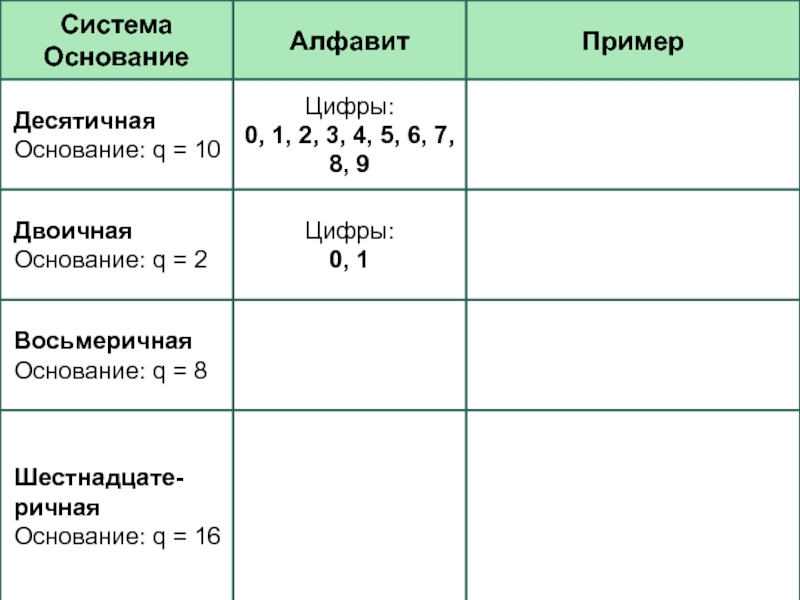
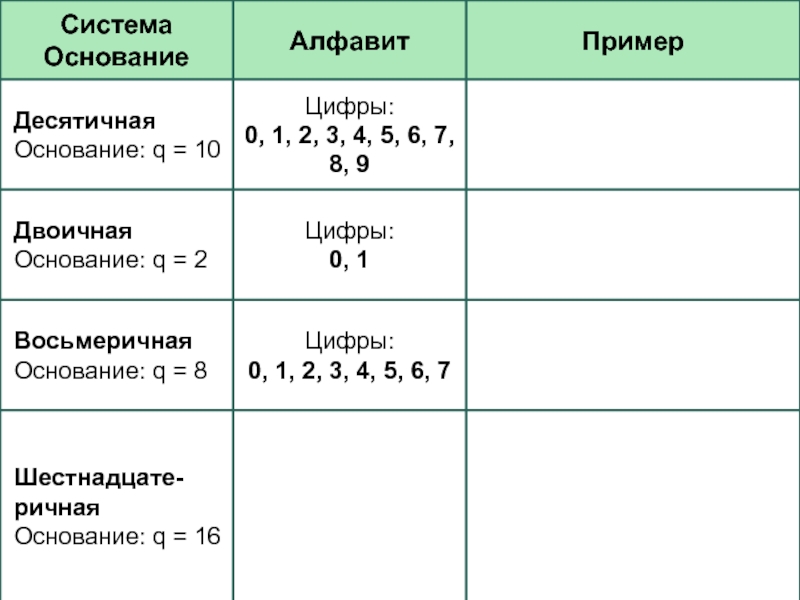
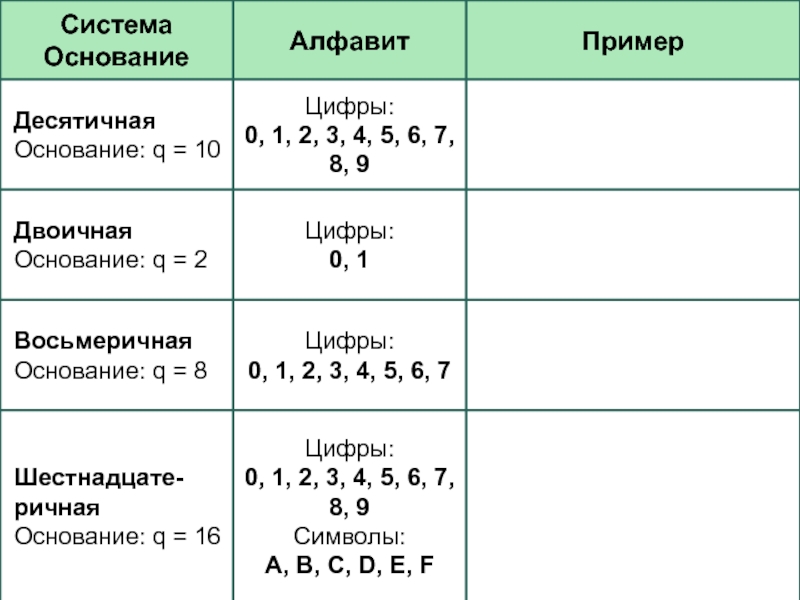
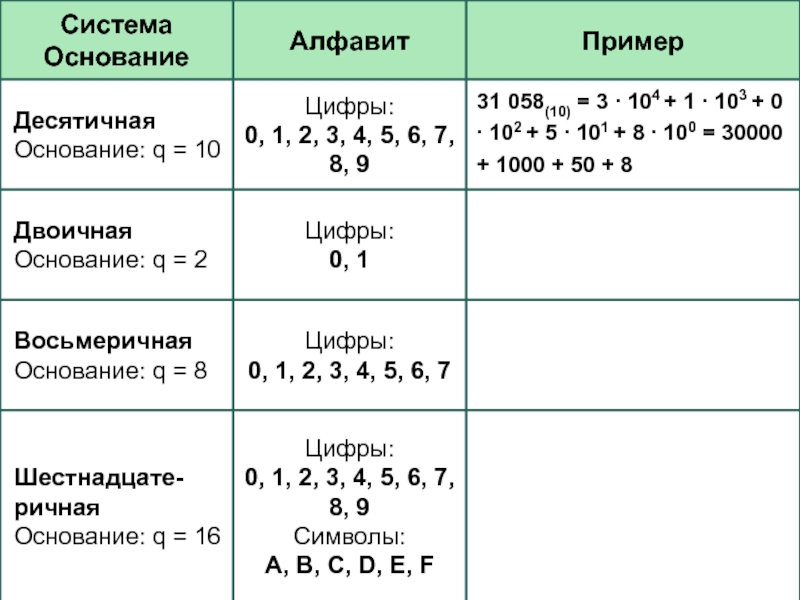
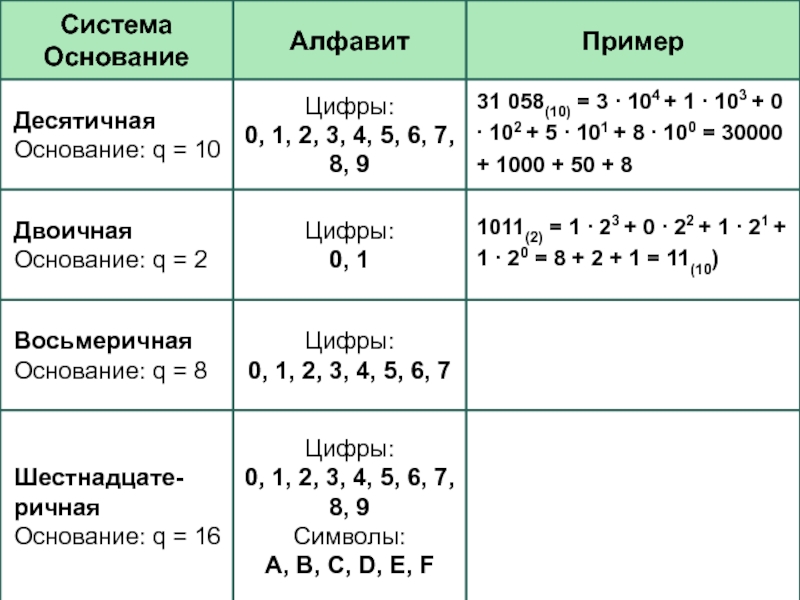
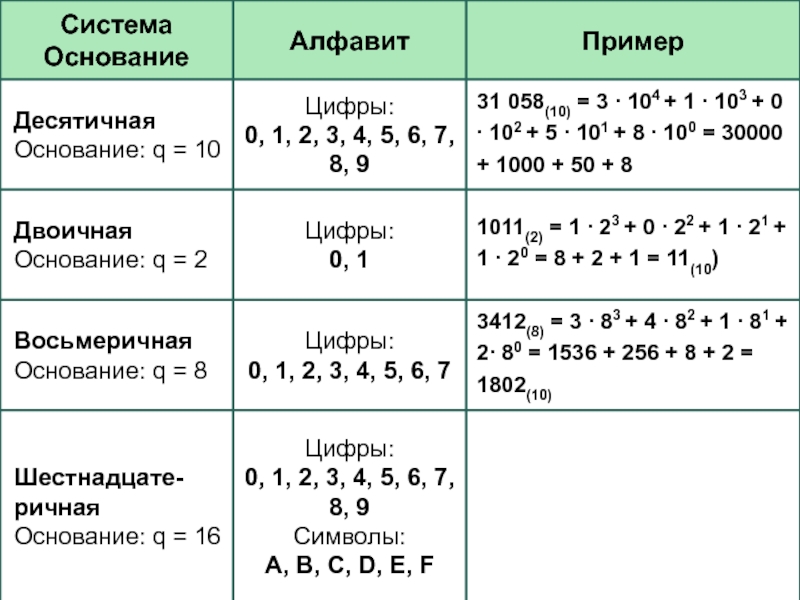
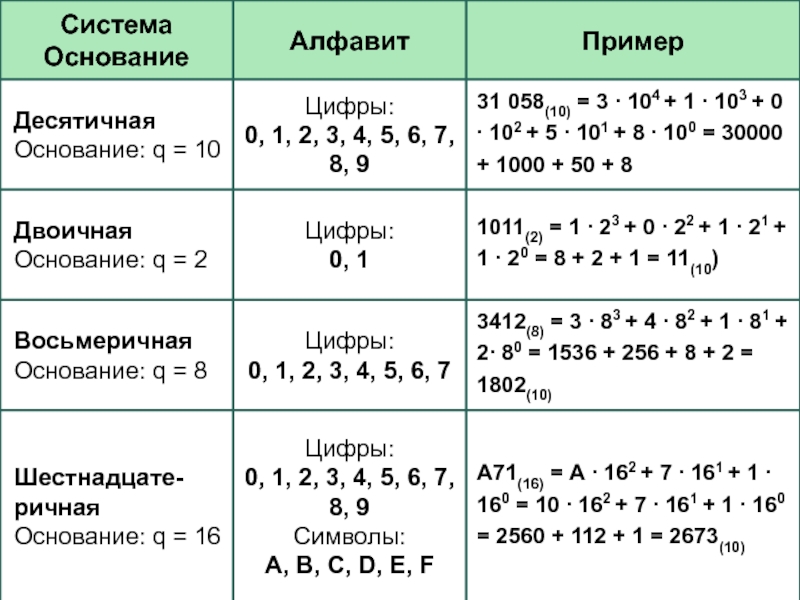
- 13. Представление первых чисел в некоторых системах счисленияq – это основание системы
- 14. Основные достоинства позиционной системы счисления:Ограниченное количество символов для записи чисел;Простота выполнения арифметических операций.
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Задание 3:Запишите в развернутой форме числа:N8 =
- 26. Двоичная система счисления1703г. – великий немецкий математик
- 27. Перевод чисел из двоичной системы счисления в
- 28. Перевод целых чисел из десятичной системы счисления
- 29. Перевод целых чисел из десятичной системы счисления
- 30. Перевод целых чисел из десятичной системы счисления
- 31. Перевод целых чисел из десятичной системы счисления
- 32. Перевод целых чисел из десятичной системы счисления
- 33. Перевод целых чисел из десятичной системы счисления
- 34. Перевод целых чисел из десятичной системы счисления
- 35. Перевод целых чисел из десятичной системы счисления в другие системы счисления(N10 N8, N16)
- 36. Перевод целых чисел из десятичной системы счисления
- 37. Перевод целых чисел из десятичной системы счисления
- 38. Перевод целых чисел из десятичной системы счисления
- 39. Перевод целых чисел из десятичной системы счисления
- 40. Перевод целых чисел из десятичной системы счисления
- 41. Перевод целых чисел из десятичной системы счисления
- 42. Перевод целых чисел из десятичной системы счисления
- 43. Перевод целых чисел из десятичной системы счисления
- 44. Перевод целых чисел из десятичной системы счисления
- 45. Перевод дробных чисел из десятичной системы счисления
- 46. Перевод дробных чисел из десятичной системы счисления
- 47. Перевод дробных чисел из десятичной системы счисления
- 48. Перевод дробных чисел из десятичной системы счисления
- 49. Перевод дробных чисел из десятичной системы счисления
- 50. Перевод дробных чисел из десятичной системы счисления
- 51. Перевод дробных чисел из десятичной системы счисления
- 52. Перевод дробных чисел из десятичной системы счисления
- 53. Перевод дробных чисел из десятичной системы счисления
- 54. Перевод дробных чисел из десятичной системы счисления
- 55. Перевод дробных чисел из десятичной системы счисления
- 56. Перевод дробных чисел из десятичной системы счисления
- 57. Перевод дробных чисел из десятичной системы счисления
- 58. Перевод дробных чисел из десятичной системы счисления
- 59. Перевод дробных чисел из десятичной системы счисления
- 60. Перевод дробных чисел из десятичной системы счисления
- 61. Домашнее задание №1Какие числа написаны римскими цифрами: MMMD,
- 62. Домашнее задание №2Какое минимальное основание должна иметь
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.Цифры – это знаки, используемые при записи чисел. Сами знаки составляют алфавит системы счисления.
Слайд 2Система счисления — это знаковая система, в которой числа записываются по
определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Цифры – это знаки, используемые при записи чисел. Сами знаки составляют алфавит системы счисления.
Цифры – это знаки, используемые при записи чисел. Сами знаки составляют алфавит системы счисления.
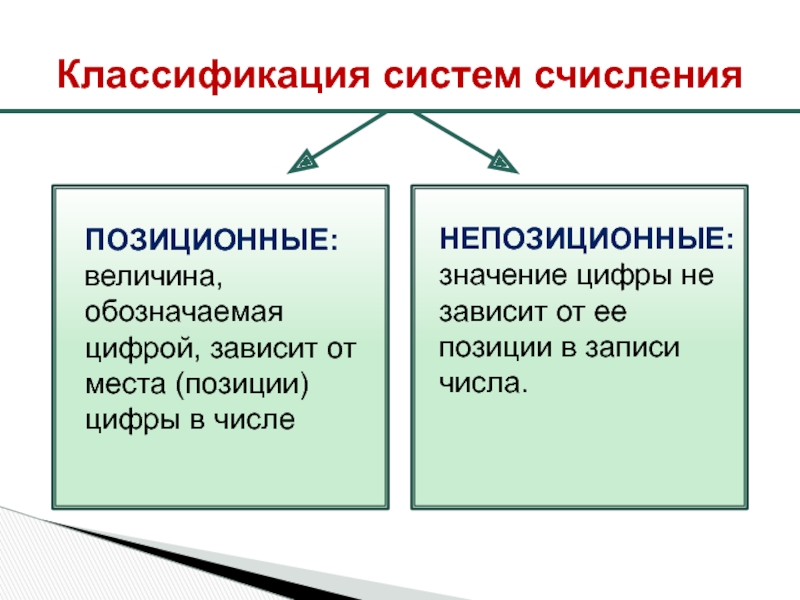
Слайд 3Классификация систем счисления
Позиционные: величина, обозначаемая цифрой, зависит от места (позиции)
цифры в числе
Непозиционные: значение цифры не зависит от ее позиции в записи числа.
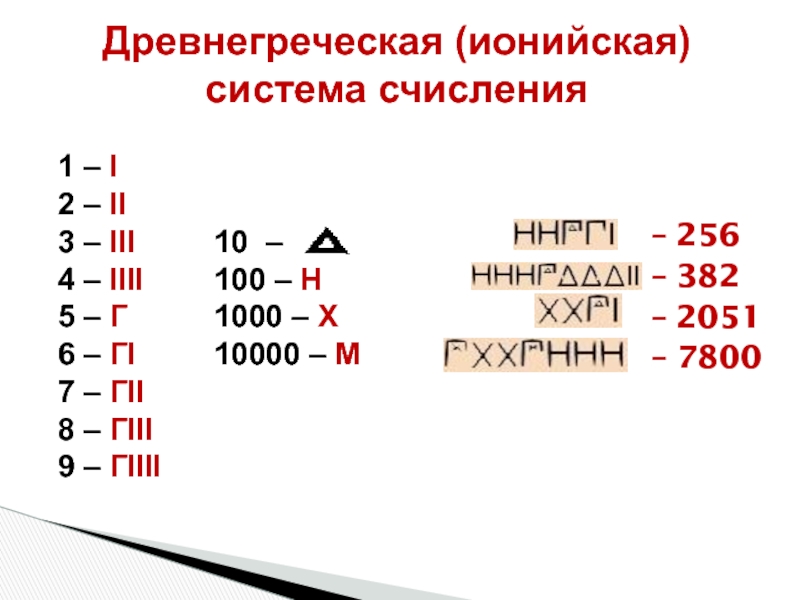
Слайд 6Древнегреческая (ионийская) система счисления
1 – I
2 – II
3 – III
4 –
IIII
5 – Г
6 – ГI
7 – ГII
8 – ГIII
9 – ГIIII
5 – Г
6 – ГI
7 – ГII
8 – ГIII
9 – ГIIII
Слайд 7Римская система счисления
1 – I
5 – V
10 – X
50 –
L
100 – C
500 – D
1000 – M
100 – C
500 – D
1000 – M
В римской системе счисления семь чисел обозначаются буквами:
Остальные числа записываются комбинацией этих знаков.
Если числа в комбинации идут от больших к меньшим, числа складываются; если от меньших к большим – значение числа вычитается из следующей буквы:
XXI = 10+10+1 = 21
MMVIII = 1000+1000+5+1+1+1 = 2008,
IV = 5-1 = 4
Слайд 8Римская система счисления
Задание 1:
Переведите числа из римской системы счисления в десятичную
– LXXXVI, XLIX, CMXCIX.
2. Запишите десятичные числа в римской системе счисления – 464, 390, 2648.
3. Где в настоящее время используется римская система счисления?
2. Запишите десятичные числа в римской системе счисления – 464, 390, 2648.
3. Где в настоящее время используется римская система счисления?
I V X L C D M
1 5 10 50 100 500 1000
Слайд 9Недостатки непозиционной системы счисления:
Для записи больших чисел необходимо вводить новые цифры
(буквы);
Трудно записывать большие числа;
Нельзя записывать дробные и отрицатель-ные числа;
Нет нуля;
Очень сложно выполнять арифметические действия.
Трудно записывать большие числа;
Нельзя записывать дробные и отрицатель-ные числа;
Нет нуля;
Очень сложно выполнять арифметические действия.
Слайд 10Позиционные системы счисления
Троичная – 0, 1, 2
Пятеричная – 0, 1, 2,
3, 4
Десятичная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двенадцатеричная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
и другие.
Позиция цифры в числе называется разрядом.
В числе 555 первая 5 стоит в позиции сотен, вторая 5 – в позиции десятков, третья 5 – в позиции единиц (555=500+50+5).
Десятичная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двенадцатеричная – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
и другие.
Позиция цифры в числе называется разрядом.
В числе 555 первая 5 стоит в позиции сотен, вторая 5 – в позиции десятков, третья 5 – в позиции единиц (555=500+50+5).
Слайд 11Десятичная система счисления
Начало десятичной системе счисления было положено в Древнем Египте
и Вавилоне, в основном ее формирование было завершено индийскими математиками в V-VIIвв. н.э.
Арабы первые познакомились с этой нумерацией и по достоинству ее оценили. В XII веке арабская нумерация чисел распространилась по всей Европе.
Арабы первые познакомились с этой нумерацией и по достоинству ее оценили. В XII веке арабская нумерация чисел распространилась по всей Европе.
Слайд 12Позиционные системы счисления
Основание системы – это количество различных знаков, используемых для
изображения чисел в данной системе.
Например,
3125 – основание 5 – пятеричная
3128 – основание 8 – восьмеричная
31210 – основание 5 – десятичная
Задание 2:
Укажите какие числа записаны с ошибками.
1567; 3005,234; 185,7948; 11022; 1345,526; 112,0113; 16,5455.
Слайд 14Основные достоинства позиционной системы счисления:
Ограниченное количество символов для записи чисел;
Простота выполнения
арифметических операций.
Слайд 25Задание 3:
Запишите в развернутой форме числа:
N8 = 52003 =
N2 = 110011
=
N16 = AСDЕ =
N8 = 7764,1 =
N5 = 2430,43 =
N16 = 3AF,15 =
Задание 4:
Запишите число в десятичной системе счисления:
110112=…, 423,15=…, 5А,1216=….
N16 = AСDЕ =
N8 = 7764,1 =
N5 = 2430,43 =
N16 = 3AF,15 =
Задание 4:
Запишите число в десятичной системе счисления:
110112=…, 423,15=…, 5А,1216=….
Слайд 26Двоичная система счисления
1703г. – великий немецкий математик Лейбниц ввел в математику
двоичную систему счисления.
1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем.
В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2.
1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем.
В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2.
Слайд 27Перевод чисел из двоичной системы счисления в десятичную (N2N10)
Пример:
1011,012 =
=
1 ∙ 23 + 0 ∙ 22 + 1 ∙ 21 + 1 ∙ 20 + 0 ∙ 2-1 + 1 ∙ 2-2 =
= 8 + 2 + 1 + ¼ = 8 + 2 + 1 + 0,25 = 11,25.
Задание 5:
Переведите в десятичную систему счисления
10110,0112; 110101,12 ; 10101,1012
= 8 + 2 + 1 + ¼ = 8 + 2 + 1 + 0,25 = 11,25.
Задание 5:
Переведите в десятичную систему счисления
10110,0112; 110101,12 ; 10101,1012
Слайд 28Перевод целых чисел из десятичной системы счисления в двоичную (N10
N2)
Задание
Перевести число 22 из десятичной системы в двоичную.
Слайд 30Перевод целых чисел из десятичной системы счисления в двоичную (N10
N2)
22 2
22 11 2
0 10 5
1
Слайд 31Перевод целых чисел из десятичной системы счисления в двоичную (N10
N2)
22 2
22 11 2
0 10 5 2
1 4 2
1
Слайд 32Перевод целых чисел из десятичной системы счисления в двоичную (N10
N2)
22 2
22 11 2
0 10 5 2
1 4 2 2
1 2 1
0
Слайд 33Перевод целых чисел из десятичной системы счисления в двоичную (N10
N2)
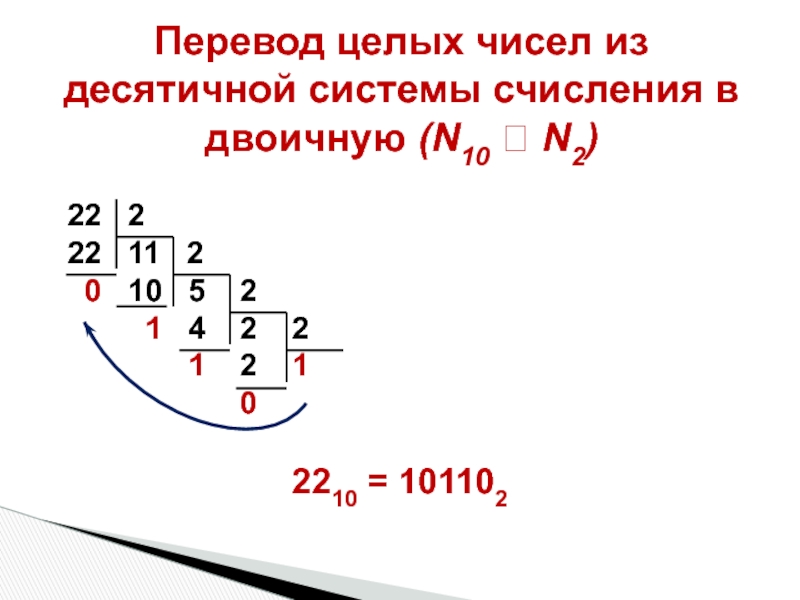
22 2
22 11 2
0 10 5 2
1 4 2 2
1 2 1
0
2210 = 101102
Слайд 34Перевод целых чисел из десятичной системы счисления в двоичную (N10
N2)
Задание 6:
Переведите числа 27; 35; 54; 66 из десятичной системы счисления в двоичную.
Слайд 35Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
Слайд 36Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получим частное меньшее делителя;
Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
Составить число в новой системе счисления, записывая его, начиная с последнего частного.
Слайд 37Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
Задание
Перевести число 158 из десятичной системы в восьмеричную, шестнадцате-ричную.
Слайд 38Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
158 8
158 19
6
Слайд 39Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
158 8
158 19 8
6 16 2
3
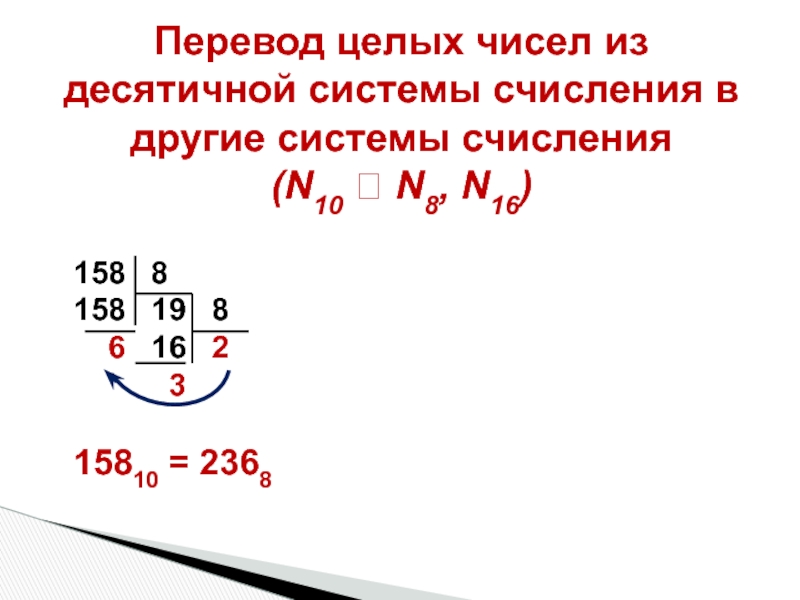
Слайд 40Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
158 8
158 19 8
6 16 2
3
15810 = 2368
Слайд 41Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
158 8 158 16
158 19 8 144 9
6 16 2 14
3
15810 = 2368
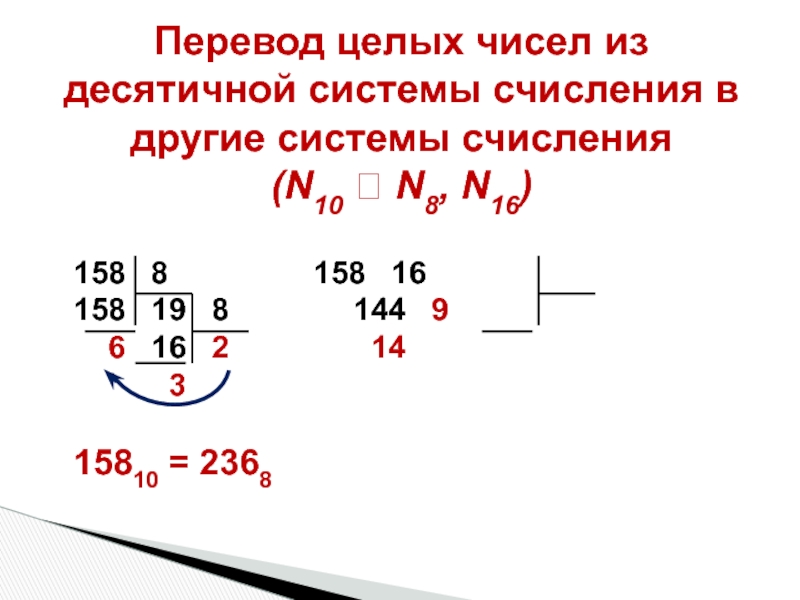
Слайд 42Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
158 8 158 16
158 19 8 144 9
6 16 2 14
3
1410 = Е16
15810 = 2368
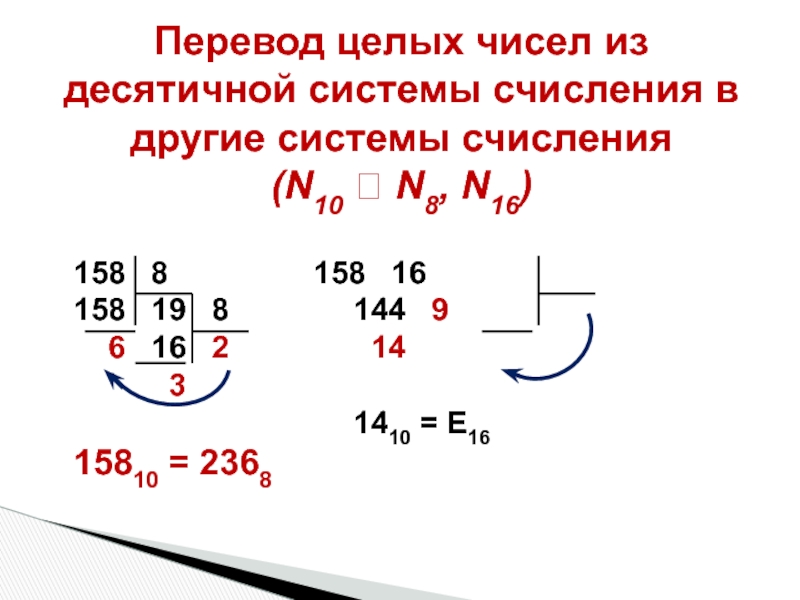
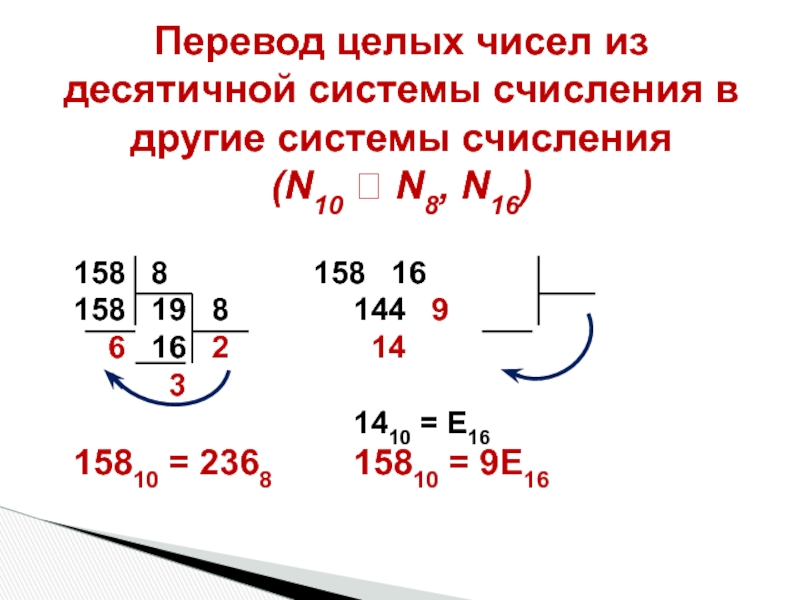
Слайд 43Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
158 8 158 16
158 19 8 144 9
6 16 2 14
3
1410 = Е16
15810 = 2368 15810 = 9Е16
Слайд 44Перевод целых чисел из десятичной системы счисления в другие системы счисления
(N10
N8, N16)
Задание 7
Перевести число 315 из десятичной системы в восьмеричную, шестнадцате-ричную.
Слайд 45Перевод дробных чисел из десятичной системы счисления в другие системы счисления
Последовательно
умножать данное число и получаемые дробные части на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа;
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести с алфавитом новой системы;
Составить дробную часть числа в новой системе, начиная с целой части первого произведения.
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести с алфавитом новой системы;
Составить дробную часть числа в новой системе, начиная с целой части первого произведения.
Слайд 46Перевод дробных чисел из десятичной системы счисления в другие системы счисления
Задание
Перевести
десятичную дробь 0,1875 из десятичной системы в двоичную, восьмеричную, шестнадцатеричную.
Слайд 47Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875
⨉ 2
0 3750
⨉ 2
0 3750
Слайд 48Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
0 3750
⨉ 2
0 7500
Слайд 49Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
1 5000
Слайд 50Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
1 0000
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
1 0000
Слайд 51Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112
⨉ 2
0 3750
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112
Слайд 52Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875
⨉ 2 ⨉ 8
0 3750 1 5000
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112
⨉ 2 ⨉ 8
0 3750 1 5000
⨉ 2
0 7500
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112
Слайд 53Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875
⨉ 2 ⨉ 8
0 3750 1 5000
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112
⨉ 2 ⨉ 8
0 3750 1 5000
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112
Слайд 54Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875
⨉ 2 ⨉ 8
0 3750 1 5000
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
⨉ 2 ⨉ 8
0 3750 1 5000
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
Слайд 55Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875 0 1875
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
Слайд 56Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875 0 1875
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000 1 1250
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000 1 1250
⨉ 2 ⨉ 8
0 7500 4 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
Слайд 57Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875 0 1875
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000 1 1250
⨉ 2 ⨉ 8 1 875
0 7500 4 0000 3 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000 1 1250
⨉ 2 ⨉ 8 1 875
0 7500 4 0000 3 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148
Слайд 58Перевод дробных чисел из десятичной системы счисления в другие системы счисления
0
1875 0 1875 0 1875
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000 1 1250
⨉ 2 ⨉ 8 1 875
0 7500 4 0000 3 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148 = 0,316
⨉ 2 ⨉ 8 ⨉ 16
0 3750 1 5000 1 1250
⨉ 2 ⨉ 8 1 875
0 7500 4 0000 3 0000
⨉ 2
1 5000
⨉ 2
1 0000
0,187510 = 0,00112 = 0,148 = 0,316
Слайд 59Перевод дробных чисел из десятичной системы счисления в другие системы счисления
Задание
8
Перевести десятичное число 315,1875 из десятичной системы в двоичную, восьмеричную, шестнадцатеричную.
Перевести десятичное число 315,1875 из десятичной системы в двоичную, восьмеричную, шестнадцатеричную.
Слайд 60Перевод дробных чисел из десятичной системы счисления в другие системы счисления
Задание
9
Перевести десятичное число 15,125 из десятичной системы в двоичную, восьмеричную, шестнадцатеричную.
Перевести десятичное число 15,125 из десятичной системы в двоичную, восьмеричную, шестнадцатеричную.
Слайд 61Домашнее задание №1
Какие числа написаны римскими цифрами:
MMMD, XIX, MMXII, CCXCVII, MCMLXXXIX?
Выполните
действия и результат запишите римскими цифрами: а) IC + XIX; б) LXVI : XI.
Запишите число в десятичной системе счисления
а) 1010112=…, б) 1305,25=…, в) 5АВ16=….
Сравните числа:
а) 1102 и 1103; б)5506 и 5058; в) Е316 и 378
Запишите число в десятичной системе счисления
а) 1010112=…, б) 1305,25=…, в) 5АВ16=….
Сравните числа:
а) 1102 и 1103; б)5506 и 5058; в) Е316 и 378
Слайд 62Домашнее задание №2
Какое минимальное основание должна иметь система счисления, если в
ней могут быть записаны числа: 21, 1201, 403, 561, 125, 874?
Перевести из десятичной системы счисления следующие числа:
а) 345 → А5; б) 6435 → А8;
в) 675 → А12; г) 98 → А2;
Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков: 0,555; 16,555; 0,333; 98,333.
Перевести из десятичной системы счисления следующие числа:
а) 345 → А5; б) 6435 → А8;
в) 675 → А12; г) 98 → А2;
Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков: 0,555; 16,555; 0,333; 98,333.
