- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике и ИКТ на тему Логические операции
Содержание
- 1. Презентация по информатике и ИКТ на тему Логические операции
- 2. Логические переменные Простые высказывания в алгебре логики обозначаются
- 3. Составные высказывания на естественном языке образуются с
- 4. Логическое умножение(конъюнкция) Составное высказывание, образованное в результате операции
- 5. Значение логической операции логического умножения задается с
- 6. Например: Определите истинность высказывания А&В, если А=«2×2=4», В=«3×3=10»А=1В=0А&В=0
- 7. Логическое сложение(дизъюнкция) Составное высказывание, образованное в результате операции
- 8. Значение логической операции логического сложения задается с
- 9. Логическое отрицание(инверсия) Логическое отрицание получает из истинного высказывания
- 10. Значение логической операции отрицания задается с помощью
- 11. Задания:Найдите значения логических выражений:а) (1∨1)∨(1∨0)=б) ((1∨0)∨1)∨1=в) (0∨1)∨(1∨0)=г) (0&1)&1=д) 1&(1&1)&1=е) ((1∨0)&(1&1))&(0∨1)=ж) ((1&0)∨(1&0))∨1=1∨1=1(1∨1)∨1=1∨1=11∨1=10&1=01&1&1=1(1&1)&1=1(0∨0)∨1=0∨1=1
- 12. Домашнее задание:Найдите значения логических выражений:((1&1)∨0)&(0∨1)((0&0)∨0)&(1∨1)
Логические переменные Простые высказывания в алгебре логики обозначаются прописными латинскими буквами. Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0.Например:А – «Два умножить на два равно 4»В – «Два умножить на два равно 5»А=1В=0
Слайд 1Логические операции
Составитель:
Гусева Анна Сергеевна,
учитель информатики и ИКТ первой квалификационной категории
Слайд 2Логические переменные
Простые высказывания в алгебре логики обозначаются прописными латинскими буквами.
Истинному
высказыванию соответствует значение логической переменной 1, а ложному – значение 0.
Например:
А – «Два умножить на два равно 4»
В – «Два умножить на два равно 5»
А=1
В=0
Слайд 3 Составные высказывания на естественном языке образуются с помощью связок «и», «или»
и «не», которые в алгебре логики заменяются на логические операции.
Логические операции задаются таблицами истинности.
Логические операции задаются таблицами истинности.
Слайд 4Логическое умножение
(конъюнкция)
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно
тогда и только тогда, когда истинны все входящие в него простые высказывания.
Конъюнкция обозначается «&» или «».
Операция конъюнкции записывается формулой:
А&В или АВ
Конъюнкция обозначается «&» или «».
Операция конъюнкции записывается формулой:
А&В или АВ
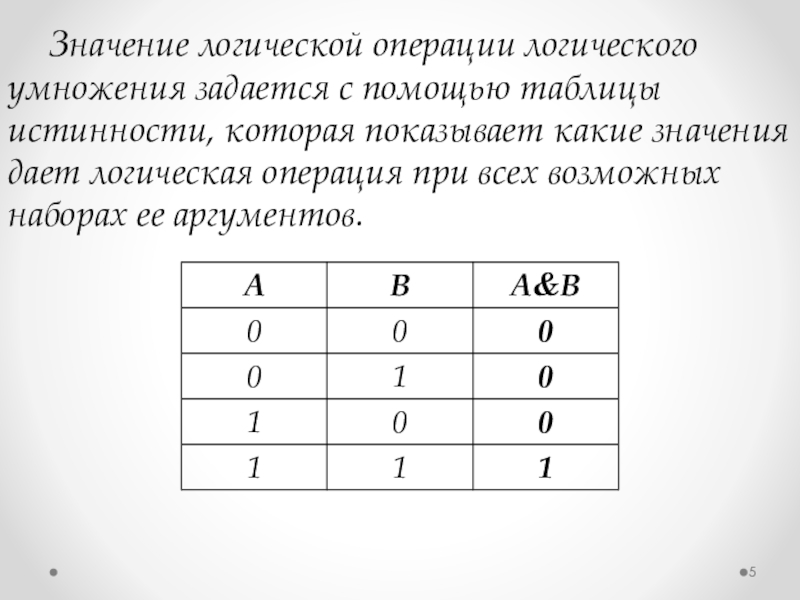
Слайд 5 Значение логической операции логического умножения задается с помощью таблицы истинности, которая
показывает какие значения дает логическая операция при всех возможных наборах ее аргументов.
Слайд 7Логическое сложение
(дизъюнкция)
Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно
тогда и только тогда, когда истинно хотя бы одно из входящих в него простые высказывания.
Дизъюнкция обозначается «∨».
Операция дизъюнкции записывается формулой:
А ∨ В
Дизъюнкция обозначается «∨».
Операция дизъюнкции записывается формулой:
А ∨ В
Слайд 8 Значение логической операции логического сложения задается с помощью таблицы истинности.
Например:
Определите
истинность высказывания А∨В, если А=«2×2=4», В=«3×3=10»
А=1
В=0
А∨В=1
Слайд 9Логическое отрицание
(инверсия)
Логическое отрицание получает из истинного высказывания ложное и, наоборот, из
ложного - истинное.
Инверсия над логическим высказыванием А обозначается « ».
Операция инверсии записывается формулой:
Инверсия над логическим высказыванием А обозначается « ».
Операция инверсии записывается формулой:
Слайд 10 Значение логической операции отрицания задается с помощью таблицы истинности.
Например:
Определите истинность
высказывания , если А=«2×2=4»
А=1
=0
Слайд 11Задания:
Найдите значения логических выражений:
а) (1∨1)∨(1∨0)=
б) ((1∨0)∨1)∨1=
в) (0∨1)∨(1∨0)=
г) (0&1)&1=
д) 1&(1&1)&1=
е) ((1∨0)&(1&1))&(0∨1)=
ж) ((1&0)∨(1&0))∨1=
1∨1=1
(1∨1)∨1=1∨1=1
1∨1=1
0&1=0
1&1&1=1
(1&1)&1=1
(0∨0)∨1=0∨1=1
