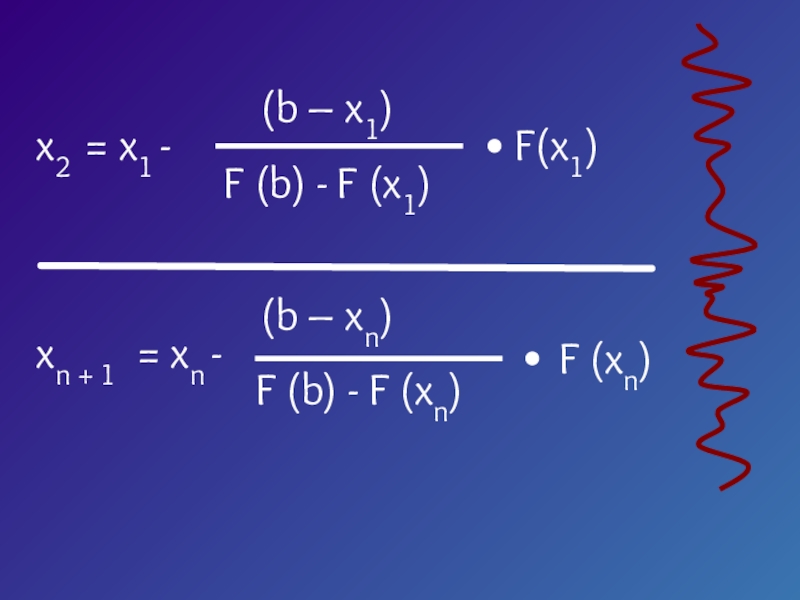Выполнили: ученицы 11 б класса
Орлова Оксана и Катанова Татьяна.
Руководитель: учитель информатики высшей квалификационной категории
Пацук Татьяна Анатольевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике и ИКТ на тему: Информационные модели
Содержание
- 1. Презентация по информатике и ИКТ на тему: Информационные модели
- 2. «Графические и численные методы решения уравнений»На языке
- 3. «Графические методы решения уравнений»Построение графиков функций может
- 4. «Численные методы решения уравнений»Численные методы решения уравнений.
- 5. Численные методы решения уравнений
- 6. методы Метод касательныхМетод половинногоМетод половинного деленияМетод хордМетод комбинированныйМетод итераций
- 7. Пусть корень ξ уравнения f (x) отделён
- 8. xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a;
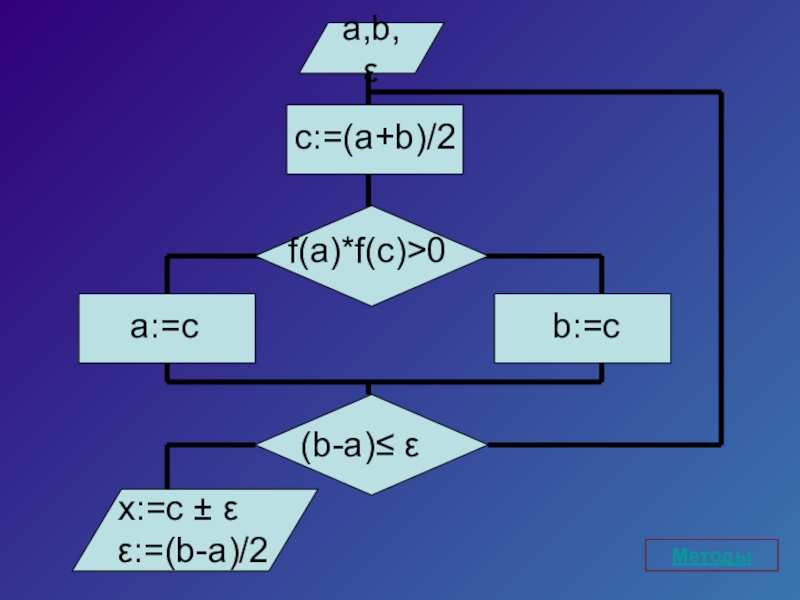
- 9. a,b, εf(a)*f(c)>0a:=cx:=c ± εε:=(b-a)/2c:=(a+b)/2b:=c(b-a)≤ εМетоды
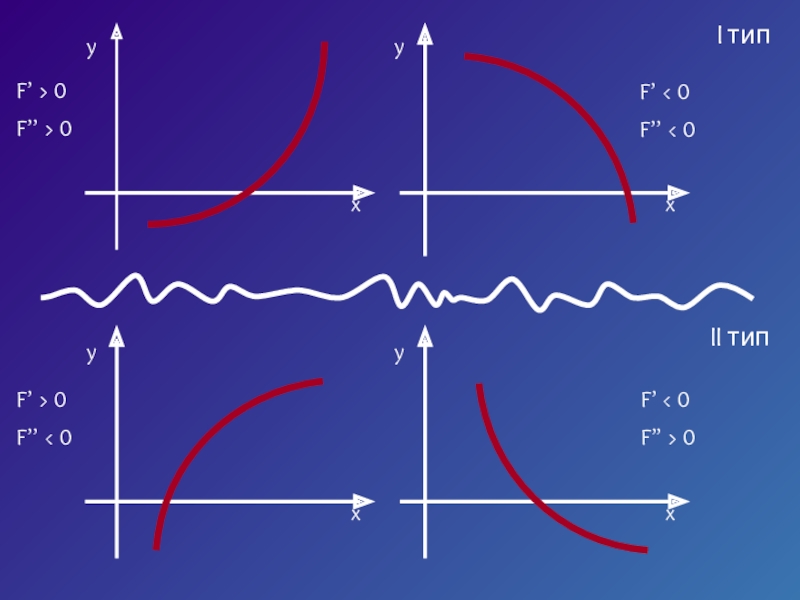
- 10. I типII тип
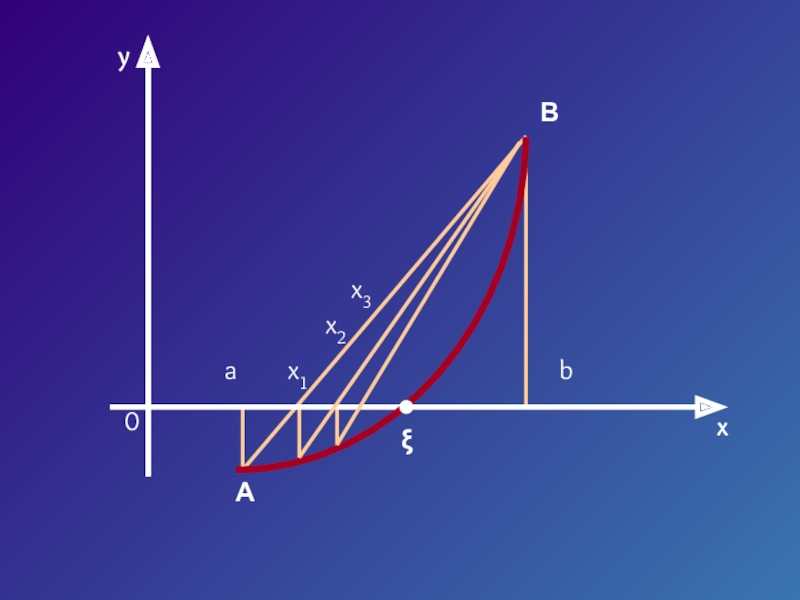
- 11. Пусть корень уравнения F (x) = 0
- 12. yx0abx1x2x3ξAB
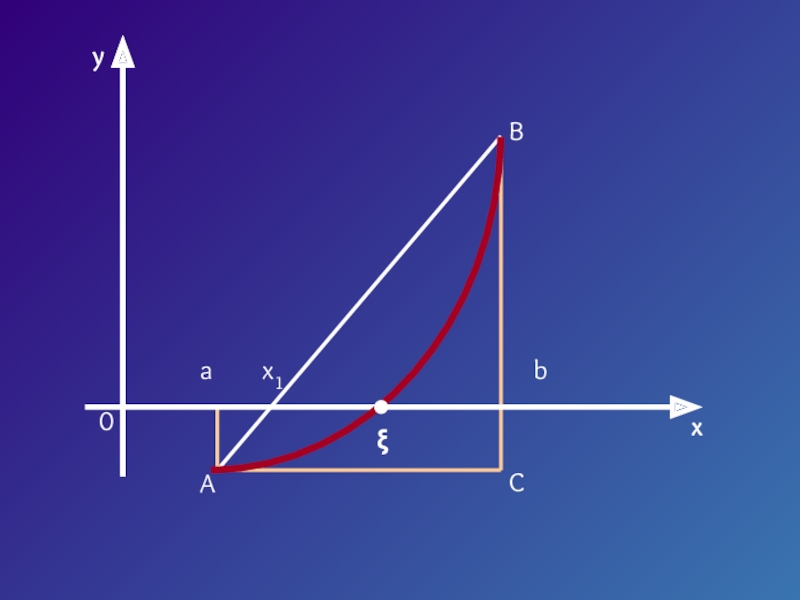
- 13. yx0abx1ξACB
- 14. Треугольник AaX1 подобен треугольнику ABCX1 – a
- 15. Слайд 15
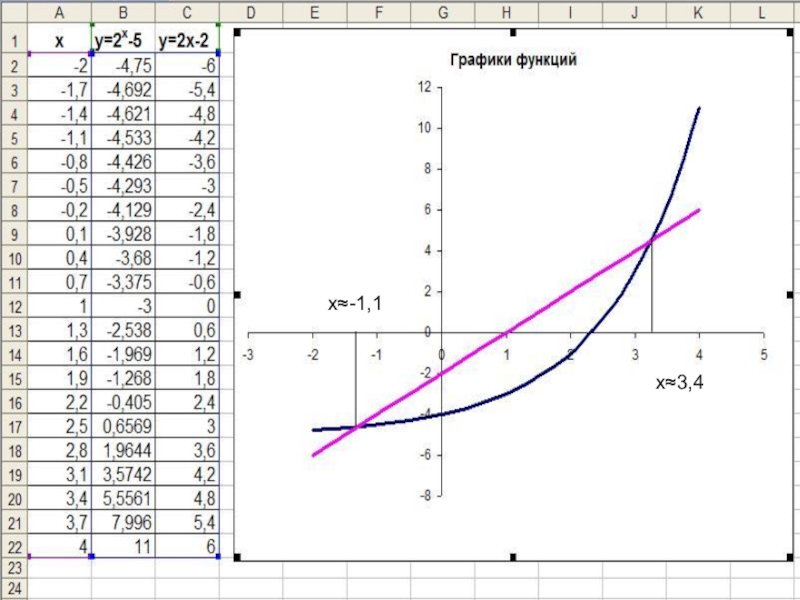
- 16. Приближенное решение уравненийc помощью электронных таблиц MS EXСEL
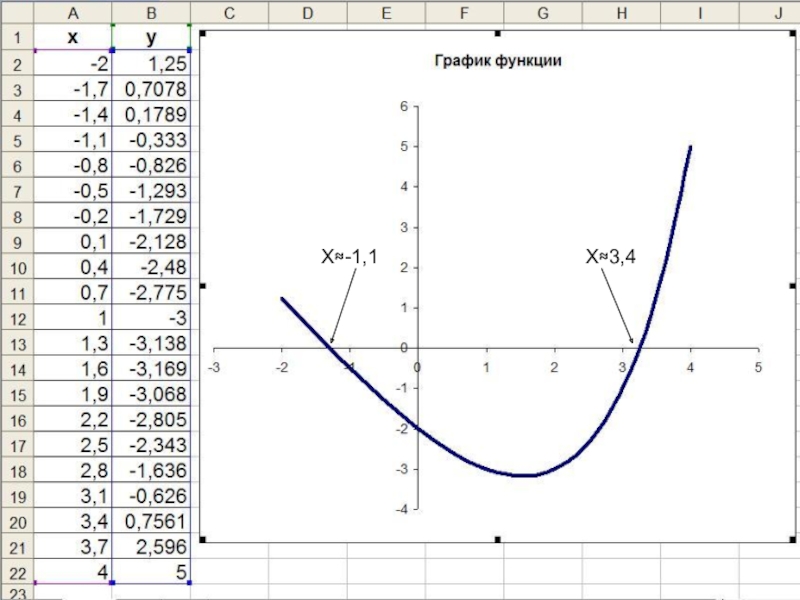
- 17. Х≈-1,1Х≈3,4
- 18. 1 способ графического решения уравнений с одним
- 19. 2 способ графического решения уравнений с одним
- 20. х≈-1,1х≈3,4
- 21. Алгоритм использования команды Подбор параметра:
- 22. Использование надстройки Подбор параметра для 1 способаПо
- 23. Графическое решение систем уравнений с двумя неизвестными
- 24. х1≈-0,5у1≈5х2≈1,5у2≈5
Слайд 1МБОУ « СОШ№1 г. Медногорска» Оренбургской области Презентация по информатике и ИКТ для
Слайд 2«Графические и численные методы решения уравнений»
На языке алгебры формальные модели записываются
Точные решения существуют только для некоторых уравнений определенного вида (линейные, квадратные, тригонометрические и др.), поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические или численные).
Слайд 3«Графические методы решения уравнений»
Построение графиков функций может использоваться для грубо приближенного
Слайд 4«Численные методы решения уравнений»
Численные методы решения уравнений. Для решения уравнений с
Слайд 6методы
Метод касательных
Метод половинногоМетод половинного деления
Метод хорд
Метод комбинированный
Метод итераций
Слайд 7Пусть корень ξ уравнения f (x) отделён на отрезке [a, b],
Будем считать, что функция:
1)Непрерывна и монотонна на отрезке [a, b]
2)f (a) x f (b) < 0
Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2
Отрезок [a, b] разделен на два отрезка [a, c] и [c, b], длина каждого = (b – a) / 2
Слайд 8x
y
a
b
c
C = (a + b) / 2
a1
b1
c1
a2
b2
c2
b-a>ε
[a; c] и [c; b],
[an; bn ], длина (b-a)/2n
(b-a)/2n <=ε
Приближенное значение корня
Cn = (an + bn) / 2 с погрешностью,
не превышающей (b-a)/2n+1
0
ξ
Слайд 11Пусть корень уравнения F (x) = 0 отделен на отрезке [a,
Будем считать:
F (x) непрерывна на отрезке [a; b]
F (x) имеет на данном отрезке производные первого и второго порядков, производные сохраняют знак.
F (a) * F (b) < 0
Слайд 181 способ графического решения уравнений с одним неизвестным
Пусть дано уравнение f(x)=g(x).
Приведем
Введем функцию у=f(x)-g(x). Построим график этой функции
Количество точек пересечения графика с осью абсцисс дает число корней уравнения
Абсциссы точек пересечения и есть решения данного уравнения
Слайд 192 способ графического решения уравнений с одним неизвестным
Пусть дано уравнение f(x)=g(x).
Введем
Построим графики этих функций в одной системе координат.
Количество точек пересечения дает число корней уравнения.
Абсциссы точек пересечения и есть решения данного уравнения.
Слайд 21
Алгоритм использования команды Подбор параметра:
Решить нужную задачу с каким – либо
Выбрать команду Подбор параметра в меню Сервис;
В появившемся окне диалога Подбор параметра в поле Установить в ячейке указывается адрес ячейки, значение в которой нужно изменить (такая ячейка называется целевой);
В поле Значение – то числовое значение, которое должно появиться в целевой ячейке;
В поле Изменяя значение ячейки ввести ссылку на ячейку с параметром
Слайд 22Использование надстройки Подбор параметра для 1 способа
По графику видно, что ближайший
Выделить ячейку В5 со значением функции и выполним команду [Сервис-Подбор параметра….]
В диалоговом окне в поле Значение: ввести требуемое значение функции (0). В поле Изменяя значение ячейки: ввести адрес $A$5, в который будет производится подбор значения аргумента. Кнопка ОК
В ячейке аргумента A5 появится подобранное значение – 1,296. Корень уравнения найден с заданной точностью.
Слайд 23Графическое решение систем уравнений с двумя неизвестными
Пусть дана система уравнений
f(x,y)=0 и y(x,y)=0
1. Рассмотрим каждое из них в виде y=f(x) и y=u(x);
2. Построим эти кривые на одном графике;
3. Определим координаты точек их пересечения, что будет являться решением исходной системы уравнений.






![Презентация по информатике и ИКТ на тему: Информационные модели Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > εБудем](/img/thumbs/ca9bab0ec7001c1f54f0524d60f56ca9-800x.jpg)
![Презентация по информатике и ИКТ на тему: Информационные модели xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a; c] и [c; b], xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a; c] и [c; b], длина отрезков (b - a) /](/img/thumbs/137923475ba250f6a87ebd34d6ee6785-800x.jpg)
![Презентация по информатике и ИКТ на тему: Информационные модели Пусть корень уравнения F (x) = 0 отделен на отрезке [a, Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b].Будем считать:F (x) непрерывна на отрезке](/img/thumbs/dcd6a89ba3c744a254bf87508e5475a1-800x.jpg)