- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике и ИКТ на тему Логические функции (10 класс)
Содержание
- 1. Презентация по информатике и ИКТ на тему Логические функции (10 класс)
- 2. АктуализацияКонъюнкция это …Дизъюнкция это …Инверсия это …Операция
- 3. ЗадачиПознакомиться с понятием «Равносильные логические выражения»Научиться доказывать
- 4. Равносильные логические выраженияРавносильными называются логические выражения, у
- 5. Равносильные логические выраженияДоказать, что логические выражения иравносильны.
- 6. Логические функцииЛюбое логическое выражение можно рассматривать как
- 7. Логические функцииОпределите по формуле2i=N,какое количество различных логических
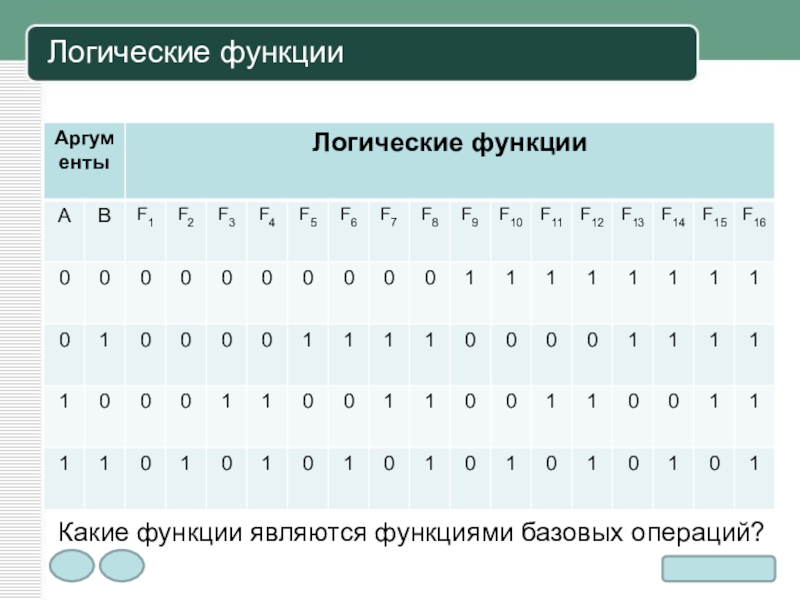
- 8. Логические функцииКакие функции являются функциями базовых операций?
- 9. ИмпликацияЛогическое следование (импликация) образуется соединением двух высказываний
- 10. ИмпликацияДля импликации не действует переместительный закон :А→В ≠ В→А.
- 11. ИмпликацияИмпликацию можно заменить на выражение, использующее только базовые операции
- 12. ЭквивалентностьЛогическое равенство (эквивалентность) образуется соединением двух высказываний
- 13. ЭквивалентностьФункция эквивалентности равносильна логическому выражению
- 14. Домашнее задание§ 3.2.2§ 3.2.3Выучить конспект
АктуализацияКонъюнкция это …Дизъюнкция это …Инверсия это …Операция логического умножения истина только тогда …Операция логического сложения истина только тогда когда …Отрицание истинного высказывания даёт …
Слайд 2Актуализация
Конъюнкция это …
Дизъюнкция это …
Инверсия это …
Операция логического умножения истина только
тогда …
Операция логического сложения истина только тогда когда …
Отрицание истинного высказывания даёт …
Операция логического сложения истина только тогда когда …
Отрицание истинного высказывания даёт …
Слайд 3Задачи
Познакомиться с понятием «Равносильные логические выражения»
Научиться доказывать равносильность логических выражений
Познакомиться с
понятием «Логическая функция»
Дать определение функции «Импликация»
Доказать, что импликацию можно выразить через базовые логические функции
Дать определение функции «Эквивалентность»
Дать определение функции «Импликация»
Доказать, что импликацию можно выразить через базовые логические функции
Дать определение функции «Эквивалентность»
Слайд 4Равносильные логические выражения
Равносильными называются логические выражения, у которых таблицы истинности совпадают.
Для
обозначения равносильных логических выражений используют знак «=»
Слайд 6Логические функции
Любое логическое выражение можно рассматривать как логическую функцию F(X1,X2,…Xn), аргументами
которой являются переменные X1,X2,…Xn.
Сама функция и аргументы могут принимать только 2 различных значения. Какие?
Сколько возможных значений будет иметь логическая функция двух аргументов?
Какое это количество информации?
Сама функция и аргументы могут принимать только 2 различных значения. Какие?
Сколько возможных значений будет иметь логическая функция двух аргументов?
Какое это количество информации?
Слайд 7Логические функции
Определите по формуле
2i=N,
какое количество различных логических функций двух аргументов может
существовать.
Каждая их этих функций будет задаваться собственной таблицей истинности.
Каждая их этих функций будет задаваться собственной таблицей истинности.
Слайд 9Импликация
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью
оборота речи «если …, то…».
Обозначается А→В.
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной посылки (первого высказывания) следует ложный вывод (второе высказывание).
Обозначается А→В.
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной посылки (первого высказывания) следует ложный вывод (второе высказывание).
Слайд 12Эквивалентность
Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью
оборота речи «… тогда и только тогда, когда …».
Обозначается А↔В или А~В.
Составное высказывание, образованное с помощью логической операции эквивалентности, истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Обозначается А↔В или А~В.
Составное высказывание, образованное с помощью логической операции эквивалентности, истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.