Презентация, доклад по информатике 10 класс Алгоритм Хаффмана

символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код.
При стандартном кодировании каждый символ кодируется 1 байтом, т.е. 8 битами.
При кодировании алгоритмом Хаффмана для любого текста можно разработать свой код.

Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами.

виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. Посмотрим, какой размер будет иметь эта строка при использовании алгоритма Хаффмана.
Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки).
Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.

бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:

создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь.

итоговое дерево:

дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:

Если мы так сделаем, то получим
следующие коды для символов:

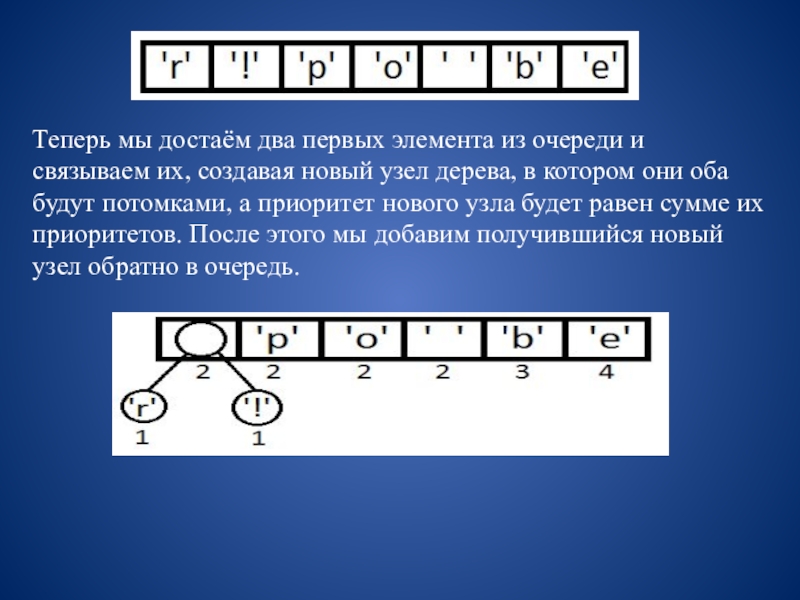
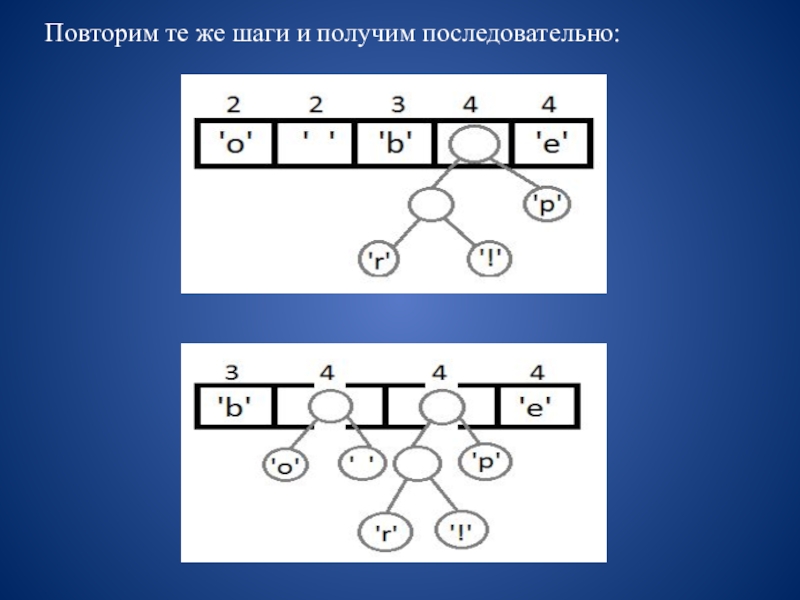
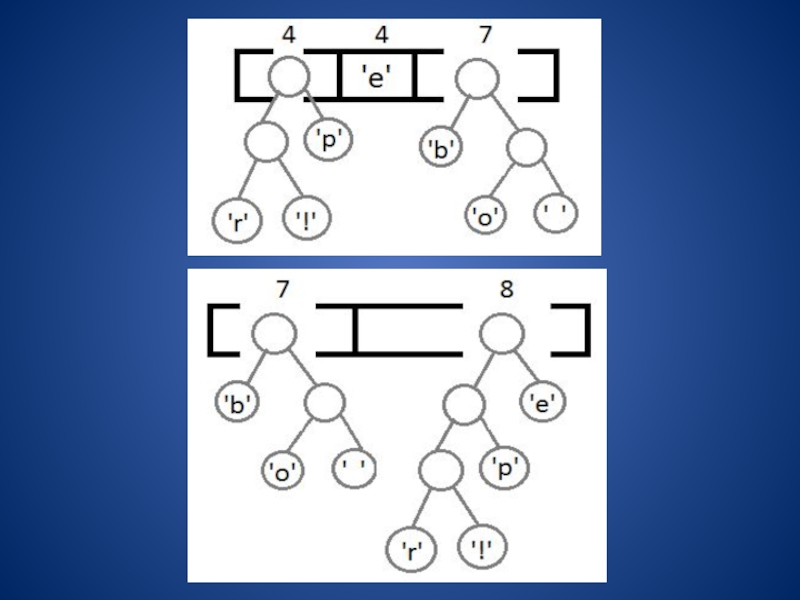
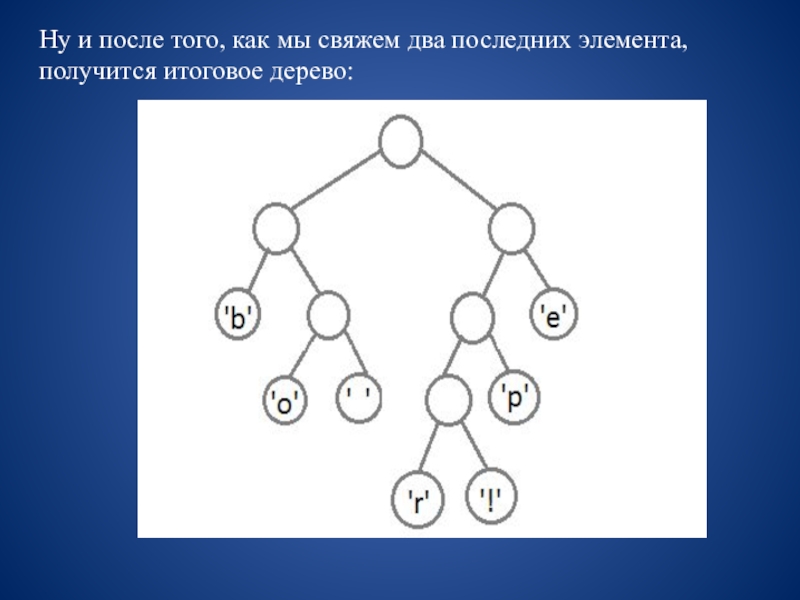
сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для 'b', то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на 'b'.

На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.

Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001» Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.