Ярослава Мудрого
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Информатика по теме Системы счисления
Содержание
- 1. Презентация по дисциплине Информатика по теме Системы счисления
- 2. Система счисления — это совокупность приемов и
- 3. Существуют позиционные и непозиционные системы счисления. В
- 4. Сама же запись числа 757,7 означает сокращенную
- 5. Продвижением цифры называют замену её следующей по
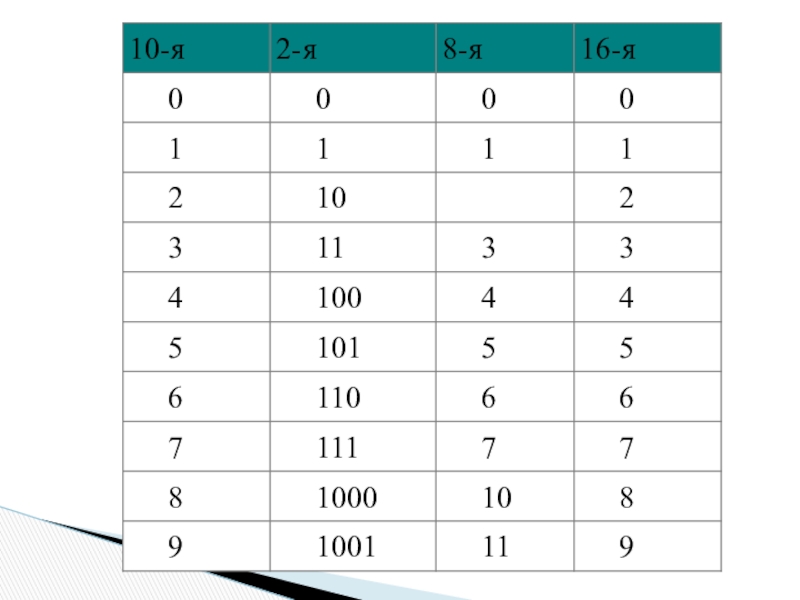
- 6. Применяя это правило, запишем первые десять целых
- 7. Слайд 7
- 8. Слайд 8
- 9. Компьютеры используют двоичную систему потому, что она
- 10. - возможно применение аппарата булевой алгебры для
- 11. Двоичная система, удобная для компьютеров, для человека
- 12. Перевод восьмеричных и шестнадцатеричных чисел в двоичную
- 13. Чтобы перевести число из двоичной системы в
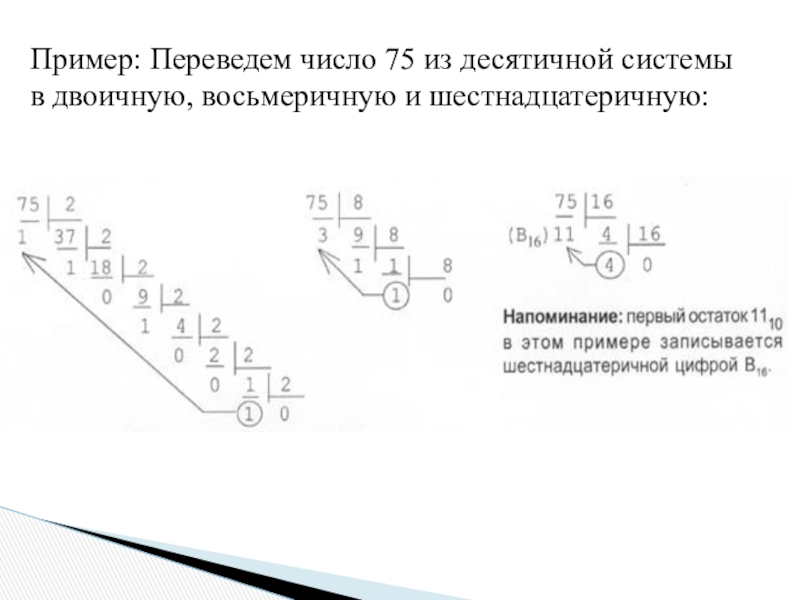
- 14. Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
- 15. Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
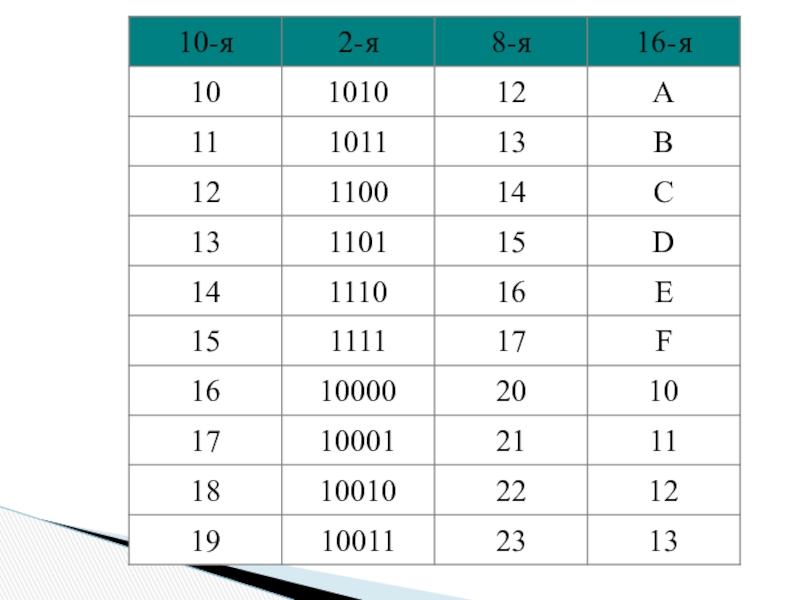
- 16. Сводная таблица переводов целых чисел:
- 17. Сводная таблица переводов целых чисел:
- 18. Сводная таблица переводов целых чисел:
Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются. Основание системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.
Слайд 1Системы счисления
Дисциплина «Информатика»
1 курс
Алексеева Юлия Владимировна
Преподаватель информатики
Политехнический колледж
Новгородского Государственного Университета
имени
Слайд 2Система счисления — это совокупность приемов и правил, по которым числа
записываются и читаются.
Основание системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.
Основание системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.
Слайд 3Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес
цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Слайд 4Сама же запись числа 757,7 означает сокращенную запись выражения
700 +
50 + 7 + 0,7 = 7 . 102 + 5 . 101 + 7 . 100 + 7 . 10—1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Любая позиционная система счисления характеризуется своим основанием.
Слайд 5Продвижением цифры называют замену её следующей по величине.
Продвинуть цифру 1 значит
заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Слайд 6Применяя это правило, запишем первые десять целых чисел
в двоичной системе:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Слайд 9Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед
другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
Слайд 10- возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Слайд 11Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости
и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина.
Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины.
Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина.
Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины.
Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Слайд 12Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления: достаточно каждую
цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:
Например:
Слайд 13Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его
нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Например,
Например,
Слайд 14Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и
шестнадцатеричную:
Слайд 15Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и
шестнадцатеричную: