- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по численным методам Численное решение уравнений с помощью электронных таблиц Microsoft Excel
Содержание
- 1. Презентация по численным методам Численное решение уравнений с помощью электронных таблиц Microsoft Excel
- 2. Введение: В общем случае процесс решения задачи
- 3. Вариант № 10 индивидуального расчетного задания
- 4. Состав задания:Ознакомиться с теоретической частью задания;Провести расчет
- 5. Постановка задачи:Пусть дано уравнение f(x) = 0,
- 6. Общая постановка задания:Найти действительные корни уравнения f(x)
- 7. Уточнение корня.Если искомый корень уравнения f(x)=0, отделен,
- 8. Индивидуальное расчетное задание
- 9. Графический методДля отделения корней уравнения естественно применять
- 10. Графический метод:X=-0,11096 ,Отрезок [-1;0]
- 11. Метод половинного деленияПостановка задачи: Пусть дано уравнение
- 12. Расчет уравнения по методу половинного деления: x=-0,11096
- 13. Метод простой итерации:
- 14. Алгоритм:Выбираем х0 из (a, b);Вычисляем;Проверяем условие, где
- 15. Слайд 15
- 16. Метод хордМетод хорд заключается в замене кривой
- 17. АлгоритмПусть k = 0;Вычислим следующий номер итерации:
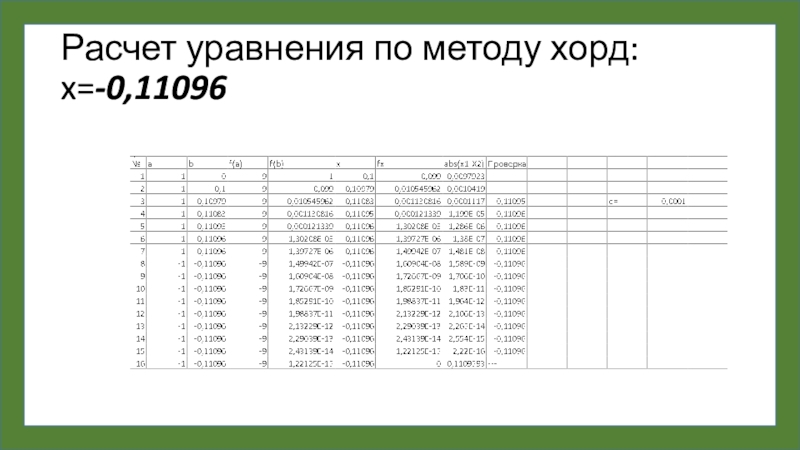
- 18. Расчет уравнения по методу хорд: x=-0,11096
- 19. Метод касательных
- 20. Расчетное уравнение по методу касательных: x=-0,11096
- 21. Вывод:Численное решение уравнений с помощью электронных таблиц
- 22. Список использованной литературы и интернет-источниковЗенков, А.В. ЧИСЛЕННЫЕ
Введение: В общем случае процесс решения задачи с использованием ЭВМ состоит из следующих этапов:1.Постановка задачи и построение математической модели (этап моделирования);2.Выбор метода и разработка алгоритма (этап алгоритмизации);3.Запись алгоритма на языке, понятном ЭВМ (этап программирования);4.Отладка и использования
Слайд 1
Численное решение уравнений с помощью электронных таблиц Microsoft Excel
Выполнила Соколова М.А.
Слайд 2Введение:
В общем случае процесс решения задачи с использованием ЭВМ состоит
из следующих этапов:
1.Постановка задачи и построение математической модели (этап моделирования);
2.Выбор метода и разработка алгоритма (этап алгоритмизации);
3.Запись алгоритма на языке, понятном ЭВМ (этап программирования);
4.Отладка и использования программы на ЭВМ (этап реализации);
5.Анализ полученных результатов (этап интерпретации).
1.Постановка задачи и построение математической модели (этап моделирования);
2.Выбор метода и разработка алгоритма (этап алгоритмизации);
3.Запись алгоритма на языке, понятном ЭВМ (этап программирования);
4.Отладка и использования программы на ЭВМ (этап реализации);
5.Анализ полученных результатов (этап интерпретации).
Слайд 4Состав задания:
Ознакомиться с теоретической частью задания;
Провести расчет для своего варианта индивидуального
задания в Microsoft Excel
Оформить презентацию в Ms Power Point , включающую:
постановку задачи;
алгоритм расчета;
таблицу с расчетом из Ms Excel, график исходной функции;
результат расчета и его анализ.
Оформить презентацию в Ms Power Point , включающую:
постановку задачи;
алгоритм расчета;
таблицу с расчетом из Ms Excel, график исходной функции;
результат расчета и его анализ.
Слайд 5Постановка задачи:
Пусть дано уравнение f(x) = 0, (a, b) - интервал, на
котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью.
Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов.
Слайд 6Общая постановка задания:
Найти действительные корни уравнения f(x) =0 ,
где f(x)
–алгебраическая или трансцендентная функция.
Точные методы решения уравнений подходят только к узкому классу уравнений ( квадратные, биквадратные,
некоторые тригонометрические, показательные, логарифмические)
Задача численного нахождения корней уравнения
состоит из двух этапов:
Отделение(локализация) корня;
Приближенное вычисление корня до заданной точности
(уточнение корней).
Точные методы решения уравнений подходят только к узкому классу уравнений ( квадратные, биквадратные,
некоторые тригонометрические, показательные, логарифмические)
Задача численного нахождения корней уравнения
состоит из двух этапов:
Отделение(локализация) корня;
Приближенное вычисление корня до заданной точности
(уточнение корней).
Слайд 7Уточнение корня.
Если искомый корень уравнения f(x)=0, отделен, т.е. определен
отрезок [a,b],
на котором существует только один действительный корень уравнения, то далее необходимо найти приближенное значение коня с заданной точностью.
Такая задача называется уточнение корня.
Уточнение корня можно производить различными методами:
Метод половинного деления(бисекции);
Метод итераций;
Метод хорд(секущих);
Метод касательных(Ньютона);
Комбинированные методы.
Такая задача называется уточнение корня.
Уточнение корня можно производить различными методами:
Метод половинного деления(бисекции);
Метод итераций;
Метод хорд(секущих);
Метод касательных(Ньютона);
Комбинированные методы.
Слайд 9Графический метод
Для отделения корней уравнения естественно применять графический метод. График функции
у = f (х) с учетом свойств функции дает много информации для определения числа корней уравнения f (х) = 0.
До настоящего времени графический метод предлагалось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т. е. методы последовательных приближений для уточнения значения корня. С появлением математических пакетов и электронных таблиц стало возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью.
Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:
1) если функция f(x) на концах отрезка [а,b] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз);
2) повторим действия предыдущего пункта для полученного отрезка.
Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.
До настоящего времени графический метод предлагалось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т. е. методы последовательных приближений для уточнения значения корня. С появлением математических пакетов и электронных таблиц стало возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью.
Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:
1) если функция f(x) на концах отрезка [а,b] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз);
2) повторим действия предыдущего пункта для полученного отрезка.
Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.
Слайд 11Метод половинного деления
Постановка задачи: Пусть дано уравнение f(x) = 0, (a,
b) - интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью.
Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов.
Метод половинного деления или дихотомии (дихотомия - сопоставленность или противопоставленность двух частей целого): Метод основан на той идее, что корень лежит либо на середине интервала (a, b), либо справа от середины, либо - слева, что следует из существования единственного корня на интервале (a, b).
Алгоритм для программной реализации:
а:=левая граница b:= правая граница
m:= (a+b)/2 середина
определяем f(a) и f(m)
если f(a)*f(m)<0 то b:=m иначе a:=m
если (a-b)/2>e повторяем , начиная с пункта2
m- искомый корень.
Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов.
Метод половинного деления или дихотомии (дихотомия - сопоставленность или противопоставленность двух частей целого): Метод основан на той идее, что корень лежит либо на середине интервала (a, b), либо справа от середины, либо - слева, что следует из существования единственного корня на интервале (a, b).
Алгоритм для программной реализации:
а:=левая граница b:= правая граница
m:= (a+b)/2 середина
определяем f(a) и f(m)
если f(a)*f(m)<0 то b:=m иначе a:=m
если (a-b)/2>e повторяем , начиная с пункта2
m- искомый корень.
Слайд 14Алгоритм:
Выбираем х0 из (a, b);
Вычисляем;
Проверяем условие, где q=(M-m)/(M+m) ;
Если оно ложно,
то переходим к пункту 7;
х0=х1;
Переходим к пункту 2;
х1–искомый корень.
х0=х1;
Переходим к пункту 2;
х1–искомый корень.
Слайд 16Метод хорд
Метод хорд заключается в замене кривой у = f(x) отрезком
прямой, проходящей через точки (а, f(a)) и (b, f(b)) . Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение.
Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая у к нулю, найдем х:
Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая у к нулю, найдем х:
Слайд 17Алгоритм
Пусть k = 0;
Вычислим следующий номер итерации: k = k +
1.
Найдем очередное k-e приближение по формуле:xk = a - f(a)(b - a)/(f(b) - f(a)). Вычислим f(xk);
Если f(xk)= 0 (корень найден), то переходим к п. 5.
Если f(xk) ×f(b)>0, то b = xk, иначе a = xk;
Если |xk – xk-1| > ε, то переходим к п. 2;
Выводим значение корня xk;
Конец.
Найдем очередное k-e приближение по формуле:xk = a - f(a)(b - a)/(f(b) - f(a)). Вычислим f(xk);
Если f(xk)= 0 (корень найден), то переходим к п. 5.
Если f(xk) ×f(b)>0, то b = xk, иначе a = xk;
Если |xk – xk-1| > ε, то переходим к п. 2;
Выводим значение корня xk;
Конец.
Слайд 21Вывод:
Численное решение уравнений с помощью электронных таблиц Microsoft Excel можно получить
различными методами:
Графический метод;
Метод половинного деления;
Метод хорд ;
Метод касательных;
Метод простой итераций.
Графический метод;
Метод половинного деления;
Метод хорд ;
Метод касательных;
Метод простой итераций.
Слайд 22Список использованной литературы и интернет-источников
Зенков, А.В. ЧИСЛЕННЫЕ МЕТОДЫ /А.В. Зенков. —
Екатеринбург: Издательство Уральского университета, 2016. — 127с.
Вычислительные методы // Википедия. [2010—2019]. Дата обновления: 31.01.2019. URL: https://ru.wikipedia.org/?oldid=97827303 (дата обращения: 20.05.2019);
Численное решение уравнений // Википедия. [2010—2018]. Дата обновления: 01.01.2018. URL: https://ru.wikipedia.org/?oldid=89982922 (дата обращения: 20.05.2019);
Вычислительные методы // Википедия. [2010—2019]. Дата обновления: 31.01.2019. URL: https://ru.wikipedia.org/?oldid=97827303 (дата обращения: 20.05.2019);
Численное решение уравнений // Википедия. [2010—2018]. Дата обновления: 01.01.2018. URL: https://ru.wikipedia.org/?oldid=89982922 (дата обращения: 20.05.2019);






![Презентация по численным методам Численное решение уравнений с помощью электронных таблиц Microsoft Excel Уточнение корня.Если искомый корень уравнения f(x)=0, отделен, т.е. определен отрезок [a,b], Уточнение корня.Если искомый корень уравнения f(x)=0, отделен, т.е. определен отрезок [a,b], на котором существует только один действительный](/img/tmb/5/498512/cba115e17f1230c08b2130c53dd3ebc0-800x.jpg)


![Презентация по численным методам Численное решение уравнений с помощью электронных таблиц Microsoft Excel Графический метод:X=-0,11096 ,Отрезок [-1;0] Графический метод:X=-0,11096 ,Отрезок [-1;0]](/img/thumbs/302c43d1887946cc093bd104b2b21b1d-800x.jpg)