- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Основы логики (8 класс)
Содержание
- 1. Презентация Основы логики (8 класс)
- 2. Логика как наука Логика (от греч.
- 3. Формы человеческого мышленияПонятие.Суждение.Умозаключение.
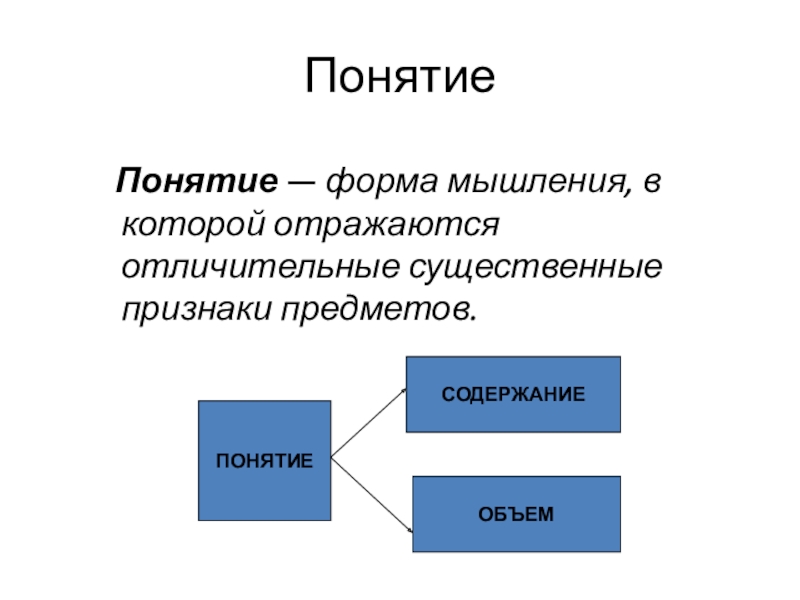
- 4. Понятие Понятие — форма мышления, в которой отражаются отличительные существенные признаки предметов.
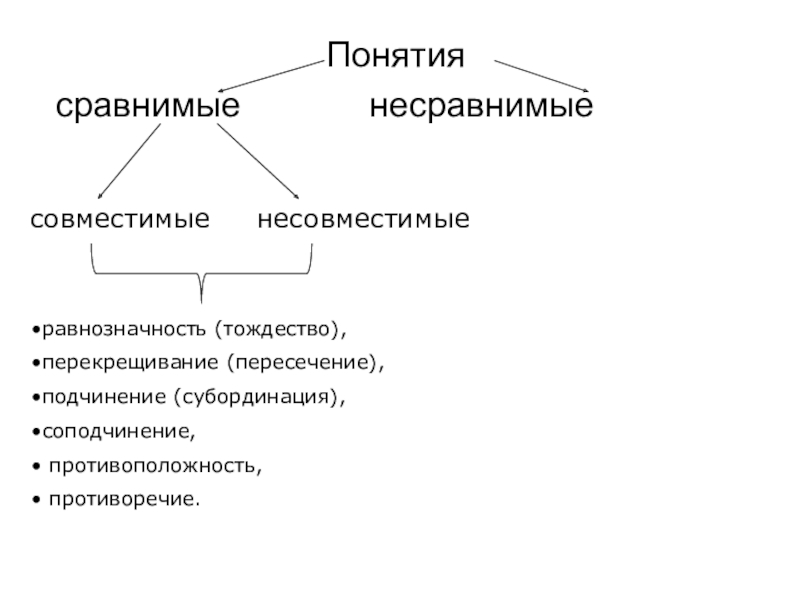
- 5. Понятия сравнимые
- 6. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми.
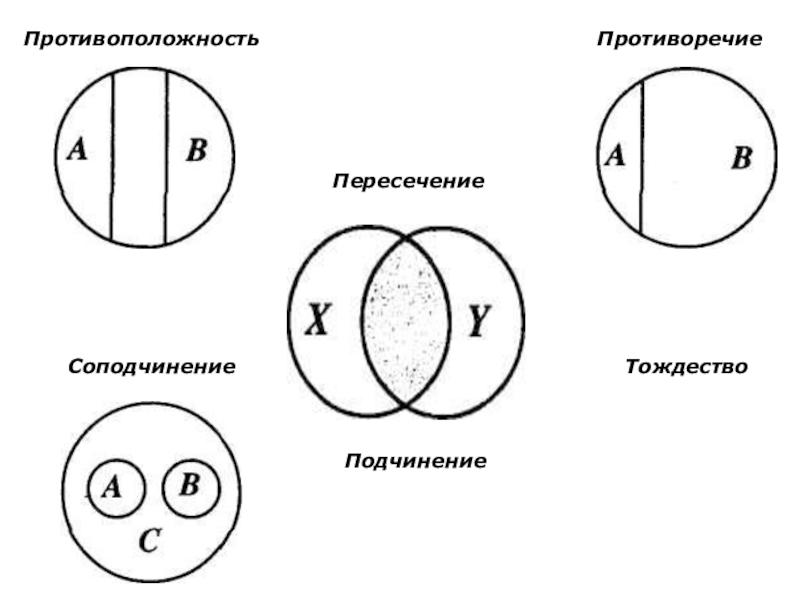
- 7. ПротивоположностьСоподчинение Противоречие ТождествоПересечениеПодчинение
- 8. Существенными называются такие признаки, каждый
- 9. Суждение Суждение (высказывание, утверждение) — форма
- 10. Умозаключение Умозаключение — форма мышления, посредством
- 11. Алгебра высказываний Алгебра логики (алгебра высказываний) —
- 12. Логические операции Логическая операция — способ построения
- 13. Логическое отрицание (инверсия) Логическое отрицание (инверсия)
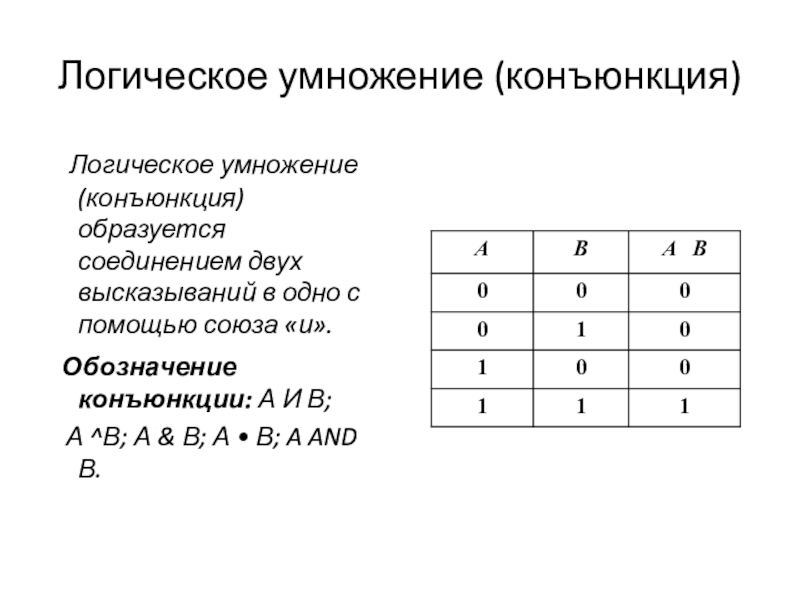
- 14. Логическое умножение (конъюнкция) Логическое умножение (конъюнкция)
- 15. Логическое сложение (дизъюнкция) Логическое сложение (дизъюнкция) образуется
- 16. Логическое следование (импликация) Логическое следование (импликация)
- 17. Логическое равенство (эквивалентность) Логическое равенство (эквивалентность)
Логика как наука Логика (от греч. logos — слово, понятие, рассуждение, разум) — наука о законах и формах рационального мышления, методах формализации содержательных теорий.
Слайд 2Логика как наука
Логика (от греч. logos — слово, понятие,
рассуждение, разум) — наука о законах и формах рационального мышления, методах формализации содержательных теорий.
Слайд 4Понятие
Понятие — форма мышления, в которой отражаются отличительные
существенные признаки предметов.
Слайд 5 Понятия
сравнимые
несравнимые
несовместимые
совместимые
равнозначность (тождество),
перекрещивание (пересечение),
подчинение (субординация),
соподчинение,
противоположность,
противоречие.
Слайд 6 Далекие друг от друга по своему содержанию понятия, не имеющие
общих признаков, называются несравнимыми.
Слайд 8 Существенными называются такие признаки, каждый из которых, взятый отдельно,
необходим, а все вместе достаточны, чтобы с их помощью отличить (выделить) данный предмет (явление) от всех остальных и сделать обобщение, объединив однородные предметы в множество.
Содержание понятия — совокупность существенных признаков, отраженных в этом понятии.
Объем понятия — множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия.
Содержание понятия — совокупность существенных признаков, отраженных в этом понятии.
Объем понятия — множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия.
Слайд 9Суждение
Суждение (высказывание, утверждение) — форма мышления, в которой что-либо
утверждается или отрицается о предметах, их свойствах или отношениях между ними.
Виды:
простые;
сложные;
истинные;
ложные
Виды:
простые;
сложные;
истинные;
ложные
Слайд 10Умозаключение
Умозаключение — форма мышления, посредством которой из одного или
нескольких суждений, называемых посылками, мы по определенным правилам вывода получаем суждение-заключение (вывод умозаключения).
Два значения:
для обозначения процесса рассуждения (размышления),
для обозначения результата этого процесса.
Два значения:
для обозначения процесса рассуждения (размышления),
для обозначения результата этого процесса.
Слайд 11Алгебра высказываний
Алгебра логики (алгебра высказываний) — раздел математической логики, изучающий
строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно оно или ложно.
Обозначать высказывания будем прописными буквами. Если высказывание А истинное, то будем писать «А = 1» и говорить «А истинно». Если высказывание А ложное, то будем писать «А = О» и говорить «А ложно».
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно оно или ложно.
Обозначать высказывания будем прописными буквами. Если высказывание А истинное, то будем писать «А = 1» и говорить «А истинно». Если высказывание А ложное, то будем писать «А = О» и говорить «А ложно».
Слайд 12Логические операции
Логическая операция — способ построения сложного высказывания из данных
высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Слайд 13Логическое отрицание (инверсия)
Логическое отрицание (инверсия) образуется из высказывания с
помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что...». Обозначение инверсии: НЕА; ¬A; ¯А ; NOT А.
Слайд 14Логическое умножение (конъюнкция)
Логическое умножение (конъюнкция) образуется соединением двух высказываний
в одно с помощью союза «и».
Обозначение конъюнкции: А И В;
А ^В; А & В; А • В; A AND В.
Обозначение конъюнкции: А И В;
А ^В; А & В; А • В; A AND В.
Слайд 15Логическое сложение (дизъюнкция)
Логическое сложение (дизъюнкция) образуется соединением двух высказываний в
одно с помощью союза «или».
Обозначение дизъюнкции: А ИЛИ В; A OR В; А \ В; А V В; А + В.
Обозначение дизъюнкции: А ИЛИ В; A OR В; А \ В; А V В; А + В.
Слайд 16Логическое следование (импликация)
Логическое следование (импликация) образуется соединением двух высказываний
в одно с помощью оборота речи «если..., то... ».
Обозначение импликации: А -> В; А => В.
Обозначение импликации: А -> В; А => В.
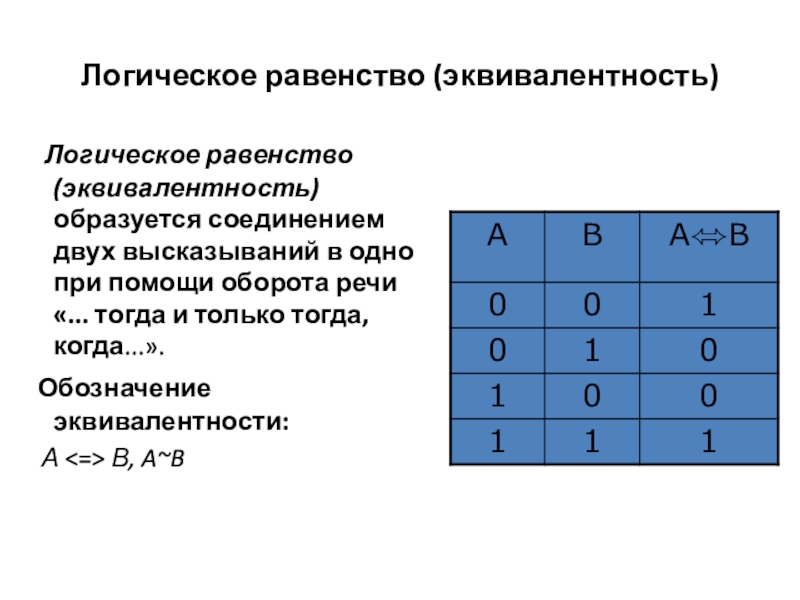
Слайд 17Логическое равенство (эквивалентность)
Логическое равенство (эквивалентность) образуется соединением двух высказываний
в одно при помощи оборота речи «... тогда и только тогда, когда...».
Обозначение эквивалентности:
А <=> В, A~B
Обозначение эквивалентности:
А <=> В, A~B