информатики
ГБОУ СОШ №249 имени М.В.Маневича
Кировского района Санкт-Петербурга
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Основные подходы к решению логических уравнений
Содержание
- 1. Презентация Основные подходы к решению логических уравнений
- 2. Кодификатор элементов содержания и требований к уровню
- 3. Необходимые знанияОбозначения, таблицы истинности, свойства логических операций
- 4. Таблицы истинности логических операций
- 5. Некоторые приемы:Замена переменных для независимых повторяющихся выраженийНаблюдения
- 6. Пример:Сколько различных решений имеет система уравненийОтвет:01 0
- 7. Пример1:Сколько различных решений имеет система уравнений ¬(x1
- 8. Пример1:Сколько различных решений имеет система уравнений (x1
- 9. Пример 2:Определить, сколько различных решений имеет система уравнений:
- 10. 2 способ(преобразовать и решать с конца)Из последнего
- 11. ЗадачаСколько существует различных наборов значений логических переменных
- 12. x1 x2 x3 x4 x5 0 1 1 1 1 0 1 1 1 0 1 1 0
- 13. Для n переменных (x1 x2x3x4… xn)уравнение имеет
- 14. y1 y2 y3 y4 y5 0 1 1 1 1 0 1 1 1 0 1 1 0 1
- 15. y1 y2 y3 y4 y50 0
- 16. матрица решенийОтвет: 31 решение.(x1→ x2) (x2→x3)
- 17. x1 x2 x3 x4 x50 0
- 18. Строим матрицу решенийОтвет: 31 решение.x1→ y1= 1 - ключ
- 19. Метод отображений(Мирончик Ел. А., Мирончик Ек. А.)МБ НОУ «Лицей №111», г. Новокузнецк
- 20. Решение логических уравненийЗадача1. Найти число решений уравнениях1
- 21. Задача1. Найти число решений уравнениях1 х2
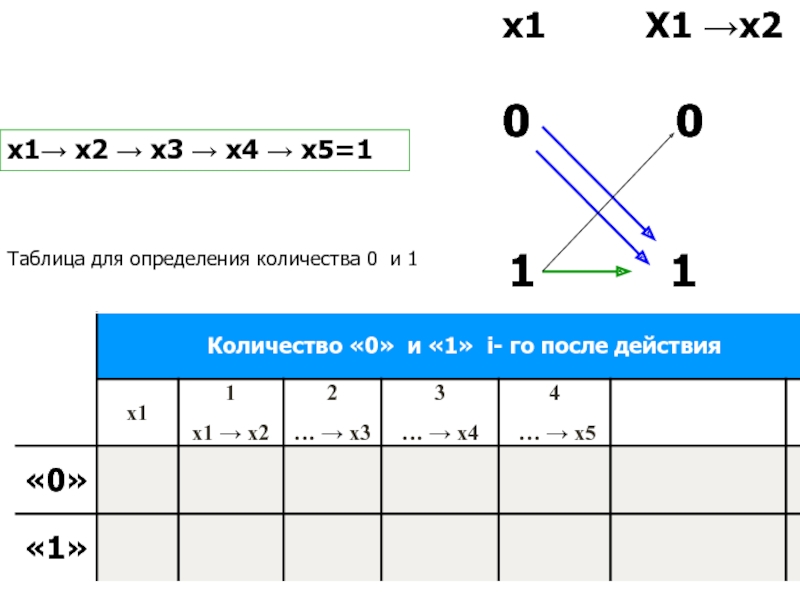
- 22. Таблица истинности для импликацииОтражение множествх1Х1 х20101
- 23. Таблица истинности для импликацииОтражение множеств
- 24. Таблица для определения количества 0 и 1х1 х2 х3 х4 х5=1
- 25. Таблица для определения количества 0 и 1х1 х2 х3 х4 х5=1Ответ:21
- 26. х1 х2 х3 х4 … х10=1
- 27. х1 х2 х3 х4 … х10=1
- 28. Слайд 28
- 29. Ответ:103 итть
- 30. -Выражения в скобках не зависят друг от
- 31. Таблица1 для первой скобки=1Таблица2
- 32. Таблица1=1Таблица2Ответ:95Всего 27 = 128 строк в таблице,Строк=0
- 33. Такое решение методом отображения хорошо подходит для уравнений, в которых каждая переменная встречается один раз.
- 34. Метод отображения для систем уравнений
- 35. Метод отображения для систем уравнений 01011011.
- 36. 0001101100011011x1x2x2x3
- 37. Пусть F(..) это функция, вычисляющая количество пар
- 38. 232F (00) = F (00)F (01) =
- 39. Система с ключевым уравнением:2.
- 40. 143F (00) = F (00)F (01) =
- 41. Система с ключевым уравнением:2.х11 по ключуF (00)
- 42. Система с ключевым уравнением:3.
- 43. 124F (00) = F (00)F (01) =
- 44. Система с ключевым уравнением:3.По ключу значения x5
- 45. 456F (00) = F (00)F (01) =
- 46. 5.52F (00) = F (00)F (01) =
- 47. 6552 решения65 решенийОтвет: 117 решенийF (00) =
- 48. 1.
- 49. 55+34+34+55 = 178 решений
- 50. 2. Сколько различных решений имеет система
- 51. 13 + 13 + 19 + 28 = 73 решения
- 52. Источники информацииhttp://kpolyakov.narod.ru/school/ege.htm, [Электронный ресурс]К.Ю. Поляков. Логические уравнения //
Кодификатор элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений для проведения единого государственного экзамена по информатике и ИКТПеречень элементов содержания, проверяемых на едином государственном экзамене по информатике и ИКТ: 1.5.1 Высказывания, логические
Слайд 1Основные подходы к решению логических уравнений.
Способы решения
систем логических уравнений
Н.М.Борисова, учитель
Слайд 2Кодификатор элементов содержания и требований к уровню подготовки выпускников общеобразовательных учреждений
для проведения единого государственного экзамена по информатике и ИКТ
Перечень элементов содержания, проверяемых на едином государственном экзамене по информатике и ИКТ:
1.5.1 Высказывания, логические операции, кванторы,
истинность высказывания
Перечень требований к уровню подготовки, проверяемому на едином государственном экзамене по информатике и ИКТ:
Код проверяемые умения
требований
1.1.7 Вычислять логическое значение сложного
высказывания по известным значениям
элементарных высказываний
Слайд 3Необходимые знания
Обозначения, таблицы истинности, свойства логических операций (конъюнкция, дизъюнкция, инверсия, эквиваленция,
исключающее «или»)
Приоритет логических операций
Законы алгебры логики
Формулы представления импликации, эквиваленции, исключающего «или»:
Приоритет логических операций
Законы алгебры логики
Формулы представления импликации, эквиваленции, исключающего «или»:
Слайд 5Некоторые приемы:
Замена переменных для независимых повторяющихся выражений
Наблюдения закономерностей роста количества решений
при добавлении переменных или уравнений
Правила комбинаторики (правила суммы и произведения)
Нет единого алгоритма решения!
Правила комбинаторики (правила суммы и произведения)
Нет единого алгоритма решения!
Слайд 6Пример:Сколько различных решений имеет система уравнений
Ответ:0
1 0 = 0
у6=0
1 0 = 0 у6=1
Решение: Решаем с конца.
Из последнего уравнения y6 y1= 0 следует, что y6=1.
Из предпоследнего уравнения х1 y6 = 0 следует, что у6=0.
Получаем противоречие, т.к. переменная у6 не может одновременно быть и 0, и 1.
Вывод- система решений не имеет.
Слайд 7Пример1:Сколько различных решений имеет система уравнений ¬(x1 ≡ x2) /\ ¬(x2 ≡
x3) =1
¬(x2 ≡ x3) /\ ¬(x3 ≡ x4) =1
...
¬(x8 ≡ x9) /\ ¬(x9 ≡ x10) =1
где x1, x2, ..., x10 – логические переменные?
¬(x1 ≡ x2) =1
¬(x2 ≡ x3) =1
…
¬(x9 ≡ x10) =1
x1 ≡ x2=0
x2 ≡ x3=0
…
x9 ≡ x10 =0
х1 х2 х3… х9 х10
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
2
x1≠x2
x2≠x3
…
x9≠x10
Слайд 8Пример1:Сколько различных решений имеет система уравнений (x1 x2) (x2
x3) =1
(x2 x3) (x3 x4) =1
...
(x8 x9) (x9 x10) =1
где x1, x2, ..., x10 – логические переменные?
х1 х2 х3… х9 х10
1 0 1 0 1 0 1 0 1 0
0 1 0 1 0 1 0 1 0 1
ответ: 2
x1≠x2
x2≠x3
…
x9≠x10
x1=x2
Слайд 102 способ(преобразовать и решать с конца)
Из последнего уравнения имеем: х1 и
х5 одного значения
x1=x5=0 или x1=x5=1 0***0 1***1
x1=x5=0 или x1=x5=1 0***0 1***1
(1)
(2)
(3)
(4)
Из уравнения (3) имеем: х4 одного значения с х1 и х5
0**00 1**11
Из уравнения (2) имеем: х3 одного значения с х1 и х4
0*000 1*111
Из уравнения (1) имеем: х2 одного значения с х1 и х3
00000 11111
Ответ: 2
Слайд 11Задача
Сколько существует различных наборов значений логических переменных x1, х2, х3, х4,
х5, y1, у2, у3, у4, у5, которые удовлетворяют всем перечисленным ниже условиям?
(x1→ x2) (x2→x3) (x3→x4) (x4→ x5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
y5 → x5 = 1.
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, х3, х4, х5, y1, у2, у3, у4, у5, при которых выполнена данная система равенств. В качестве ответа нужно указать количество таких наборов.
(x1→ x2) (x2→x3) (x3→x4) (x4→ x5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
y5 → x5 = 1.
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, х3, х4, х5, y1, у2, у3, у4, у5, при которых выполнена данная система равенств. В качестве ответа нужно указать количество таких наборов.
Слайд 12 x1 x2 x3 x4 x5
0 1 1 1 1
0 1 1 1
0 1 1
0 1
0
1 1 1 1 1
6
(x1→
x2) (x2→x3) (x3→x4) (x4→ x5) = 1;
Слайд 13 Для n переменных (x1 x2x3x4… xn)
уравнение имеет (n+1) решений
(x1→ x2)
(x2→x3) (x3→x4) …(Xn-1→ Xn) = 1;
x1 x2 x3 x4 x5
0 0 0 0 0
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
Слайд 14 y1 y2 y3 y4 y5
0 1 1 1 1
0 1 1 1
0 1 1
0 1
0
1 1 1 1 1
6
6*6=36 решений
(x1→
x2) (x2→x3) (x3→x4) (x4→ x5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
Слайд 15y1 y2 y3 y4 y5
0 0 0 0
0
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
x1 x2 x3 x4 x5
0 0 0 0 0
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
6 решений
5 решений
5 решений
5 решений
5 решений
5 решений
6+5+5+5+5+5=31
(x1→ x2) (x2→x3) (x3→x4) (x4→ x5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
y5 → x5 = 1 - ключ
Слайд 16матрица решений
Ответ: 31 решение.
(x1→ x2) (x2→x3) (x3→x4) (x4→
x5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
y5 → x5 = 1 - ключ
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
y5 → x5 = 1 - ключ
Слайд 17x1 x2 x3 x4 x5
0 0 0 0
0
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
y1 y2 y3 y4 y5
0 0 0 0 0
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
6 решений
6 решений
6 решений
6 решений
6 решений
1 решение
6+6+6+6+6+1=31
(x1→ x2) (x2→x3) (x3→x4) (x4→ x5) = 1;
(y1→ y2) (y2→y3) (y3→y4) (y4→ y5) = 1;
x1→ y1= 1 - другой ключ
Слайд 20Решение логических уравнений
Задача1. Найти число решений уравнения
х1 х2 х3
х4 х5=1
х1 х2 х3 х4 х5 х6 х7 =1
х1 х2 х3 х4 х5 … хn =1
х1 х2 х3 х4 х5 х6 х7 =1
х1 х2 х3 х4 х5 … хn =1
Слайд 21Задача1. Найти число решений уравнения
х1 х2 х3 х4
х5=1
(((х1 х2 ) х3) х4) х5=1
(((х1 х2 ) х3) х4) х5=1
1
2
3
4
Слайд 30-Выражения в скобках не зависят друг от друга;
-Таблица для второй скобки
повторяет часть таблицы для первой скобки.
Слайд 32Таблица1
=1
Таблица2
Ответ:95
Всего 27 = 128 строк в таблице,
Строк=0 всего33 (1
0 =0),
Значит остальные 128-33=95 равны 1.
Значит остальные 128-33=95 равны 1.
Слайд 33Такое решение методом отображения хорошо подходит для уравнений, в которых каждая
переменная встречается один раз.
Слайд 37Пусть F(..) это функция, вычисляющая количество пар на следующем шаге.
00
01
10
11
00
01
10
11
x1x2
x2x3
F
(00) = F (00)
F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
Слайд 38232
F (00) = F (00)
F (01) = F (00) + F
(10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
+
Ответ:232
Слайд 40143
F (00) = F (00)
F (01) = F (00) + F
(10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
Схема решения та же
Слайд 41Система с ключевым уравнением:
2.
х11 по ключу
F (00) = F (00)
F (01)
= F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
Схема решения та же
Ответ:143
Слайд 43124
F (00) = F (00)
F (01) = F (00) + F
(10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
Схема решения та же
Слайд 44Система с ключевым уравнением:
3.
По ключу значения x5 и x6 должны быть
разными.
Это значит, что в таблице в столбце x6 необходимо обнулить значения, соответствующие парам 00 и 11.
Это значит, что в таблице в столбце x6 необходимо обнулить значения, соответствующие парам 00 и 11.
F (00) = F (00)
F (01) = F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
Схема решения та же
Ответ:124
-ключ
Слайд 4765
52 решения
65 решений
Ответ: 117 решений
F (00) = F (00)
F (01) =
F (00) + F (10)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
F (10) = F (01) + F (11)
F (11) = F (01) + F (11)
Слайд 502. Сколько различных решений имеет система уравнений X1 X2
X3 = 1
X2 X3 X4 = 1
...
X8 X9 X10 = 1
Слайд 52Источники информации
http://kpolyakov.narod.ru/school/ege.htm, [Электронный ресурс]
К.Ю. Поляков. Логические уравнения // Информатика, № 14, 2011, с. 30-35.
Метод
отображения, Мирончик Е.А., МБ НОУ «Лицей №111», г. Новокузнецк
М.А. Ройтберг, д. ф.-м. н., г. Пущино, http://ege-go.ru
декабрь 2014 / ИНФОРМАТИКА Системы логических уравнений: решение с помощью битовых цепочек
М.А. Ройтберг, д. ф.-м. н., г. Пущино, http://ege-go.ru
декабрь 2014 / ИНФОРМАТИКА Системы логических уравнений: решение с помощью битовых цепочек
![Источники информацииhttp://kpolyakov.narod.ru/school/ege.htm, [Электронный ресурс]К.Ю. Поляков. Логические уравнения // Информатика, № 14, 2011, с. 30-35.Метод отображения, Мирончик Е.А., МБ НОУ «Лицей](/img/thumbs/f79154832d7d1de27ed37c8558e706c4-800x.jpg "Презентация Основные подходы к решению логических уравнений Источники информацииhttp://kpolyakov.narod.ru/school/ege.htm, [Электронный ресурс]К.Ю. Поляков. Логические уравнения // Информатика, № 14, 2011, с. 30-35.Метод")
