- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Моделирование. Системный анализ (11 класс)
Содержание
- 1. Презентация Моделирование. Системный анализ (11 класс)
- 2. Модели и моделирование
- 3. Что такое модель?Модель – это объект, который
- 4. Что такое моделирование?Моделирование – это создание и
- 5. Цели моделированияисследование оригиналаанализ («что будет, если …»)синтез («как сделать, чтобы …»)оптимизация («как сделать лучше»)
- 6. Один оригинал – одна модель?
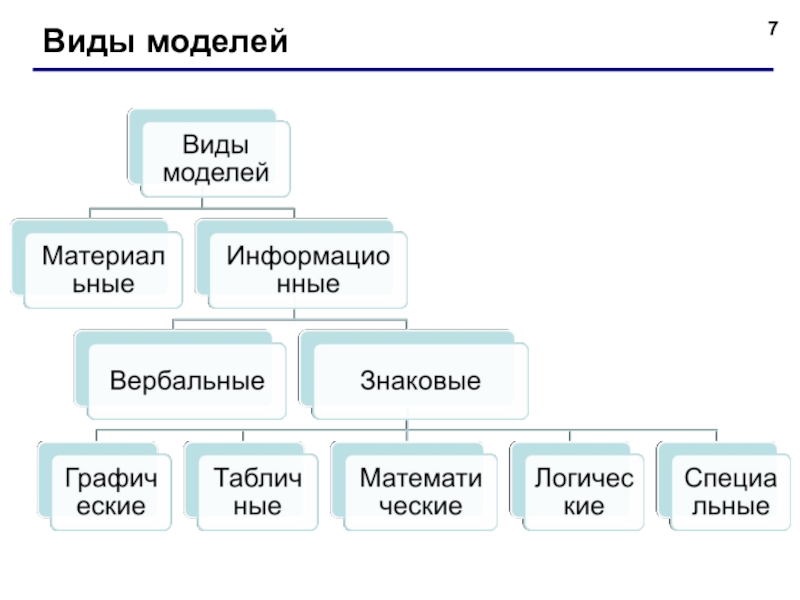
- 7. Виды моделей
- 8. ВспомнимСистемаСистемный эффект Системный анализ
- 9. Системный подход в моделированииМодель-система:Модель-не-система:1-я линия:Пр. ВетерановЛенинский пр.Автово Кировский заводНарвская…2-я линия:КупчиноЗвезднаяМосковскаяПарк ПобедыЭлектросила…
- 10. Структуры моделей системСписок ОчередьСтек Дек2. Таблица (матрица)3. Иерархия 4. Граф
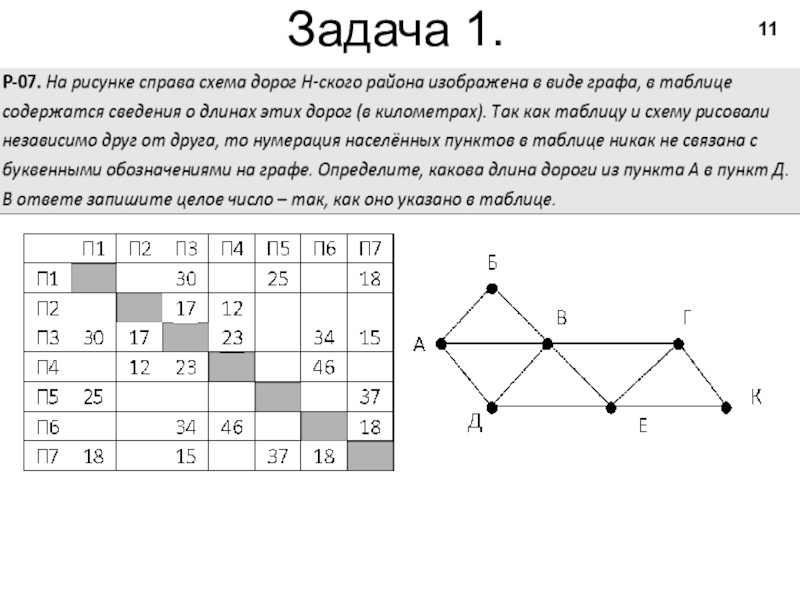
- 11. Задача 1.
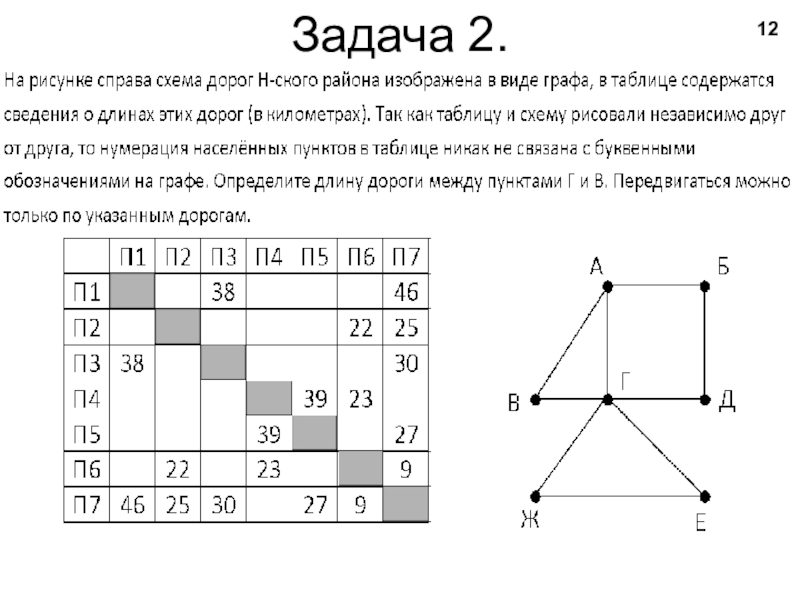
- 12. Задача 2.
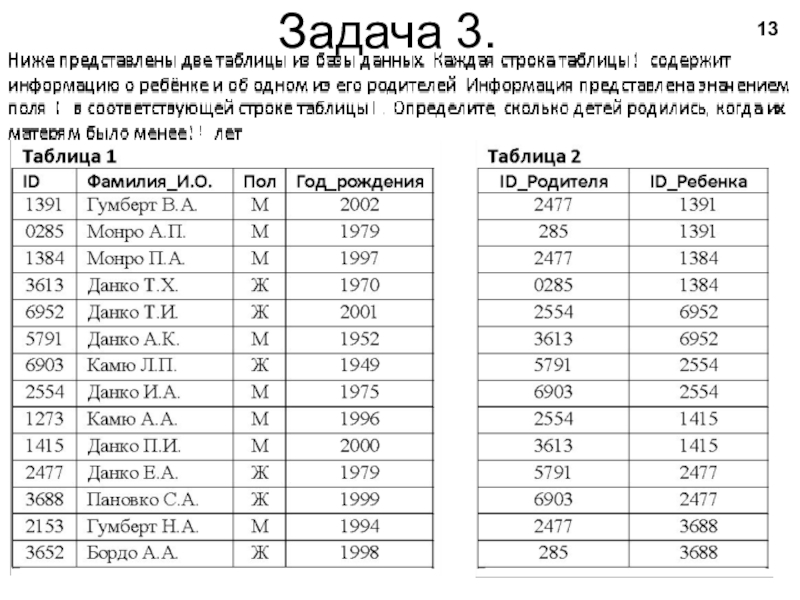
- 13. Задача 3.
- 14. Задача 4. В фрагменте базы данных представлены
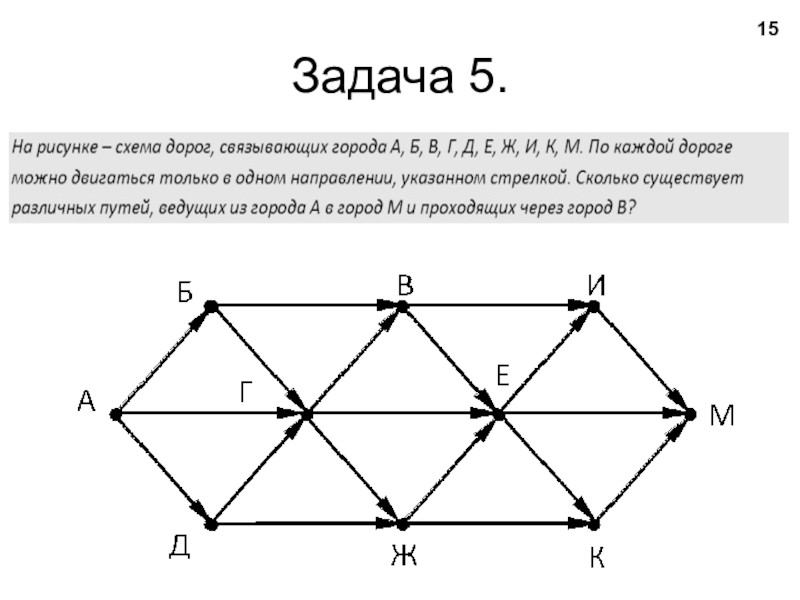
- 15. Задача 5.
- 16. Задача 6. На рисунке – схема дорог,
- 17. Задача 7. Города A, B, C и
- 18. Задача 8. Дан фрагмент электронной таблицы. Из
- 19. Задача 9.
- 20. Задача 10.
- 21. Задача 11.
- 22. Задача 12.Два игрока, Петя и Ваня играют
- 23. Задача 12. Продолжение Задание 1. а) Определите,
- 24. Задача 13. Два игрока, Петя и Ваня
- 25. Задача 14. Два игрока, Петя и Ваня,
- 26. Два игрока, Петя и Ваня играют в
- 27. . Два игрока, Петя и Ваня, играют
Модели и моделирование
Слайд 3Что такое модель?
Модель – это объект, который обладает некоторыми свойствами другого
объекта (оригинала) и используется вместо него.
Приведите примеры модели и оригинала
Приведите примеры модели и оригинала
Слайд 4Что такое моделирование?
Моделирование – это создание и использование моделей для изучения
оригиналов.
Когда используют моделирование:
оригинал не существует
исследование оригинала опасно для жизни или дорого:
оригинал сложно исследовать непосредственно:
интересуют только некоторые свойства оригинала
Когда используют моделирование:
оригинал не существует
исследование оригинала опасно для жизни или дорого:
оригинал сложно исследовать непосредственно:
интересуют только некоторые свойства оригинала
Слайд 5Цели моделирования
исследование оригинала
анализ («что будет, если …»)
синтез («как сделать, чтобы …»)
оптимизация
(«как сделать лучше»)
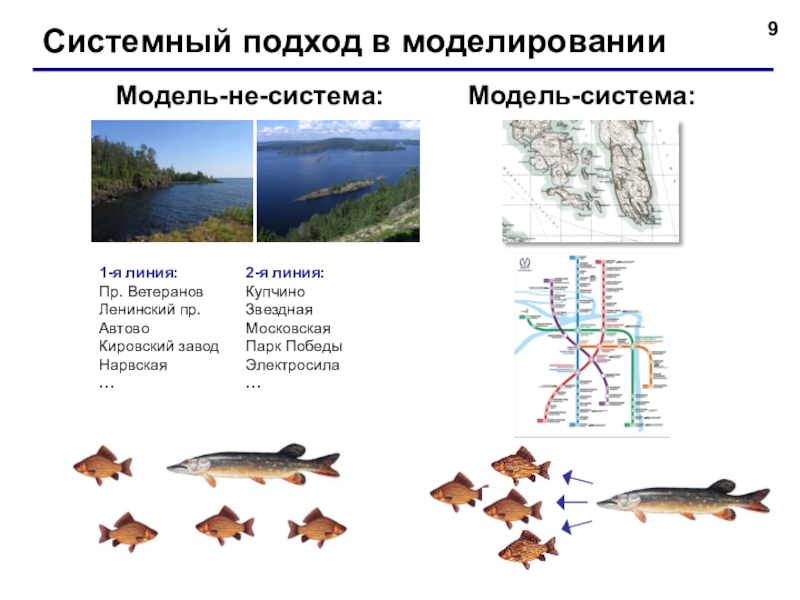
Слайд 9Системный подход в моделировании
Модель-система:
Модель-не-система:
1-я линия:
Пр. Ветеранов
Ленинский пр.
Автово
Кировский завод
Нарвская
…
2-я линия:
Купчино
Звездная
Московская
Парк Победы
Электросила
…
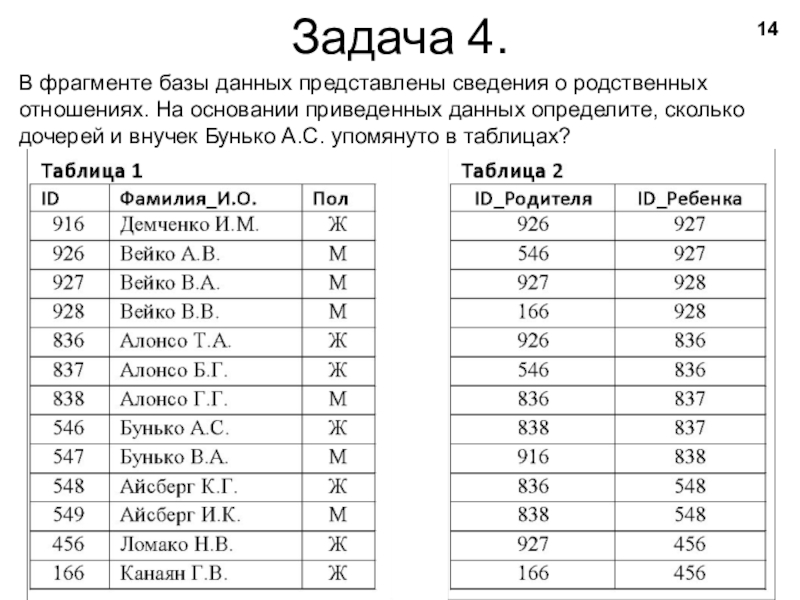
Слайд 14Задача 4.
В фрагменте базы данных представлены сведения о родственных отношениях.
На основании приведенных данных определите, сколько дочерей и внучек Бунько А.С. упомянуто в таблицах?
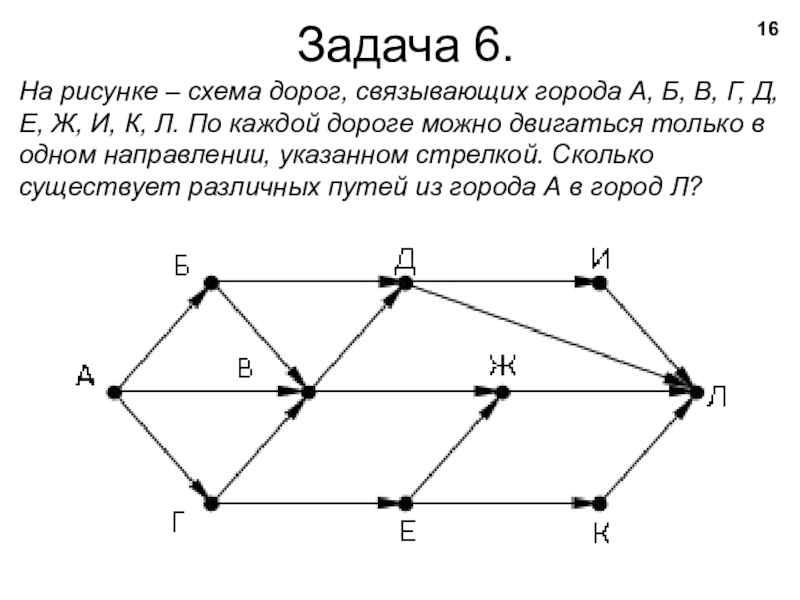
Слайд 16Задача 6.
На рисунке – схема дорог, связывающих города А, Б,
В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
Слайд 17Задача 7.
Города A, B, C и D связаны дорогами. Известно,
что существуют дороги между городами
A и С, C и B (две дороги), A и B, C и D (две дороги), B и D. Сколькими различными способами можно проехать из города А в город D, не заезжая дважды в один город?
A и С, C и B (две дороги), A и B, C и D (две дороги), B и D. Сколькими различными способами можно проехать из города А в город D, не заезжая дважды в один город?
Слайд 18Задача 8.
Дан фрагмент электронной таблицы. Из ячейки D2 в одну
из ячеек диапазона E1:E4 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились, и значение формулы стало равным 8. В какую ячейку была скопирована формула? В ответе укажите только одно число – номер строки, в которой расположена ячейка.
Слайд 22Задача 12.
Два игрока, Петя и Ваня играют в следующую игру. Задан
некоторый набор символьных цепочек («слов»), в котором ни одно слово не является началом другого (выполняется условие Фано). Игра начинается с пустой строки, в конец которой игроки по очереди дописывают буквы, по одной букве за ход так, чтобы полученная цепочка на каждом шаге была началом одного из заданных слов. Первый ход делает Петя. Выигрывает тот, кто первый составит слово из заданного набора.
Пример. Пусть заданы слова {МАК, МЫЛО, РАМА, РАК}. На первом ходу Петя может написать букву М или Р. Пусть он написал букву М. В ответ Ваня может написать А или Ы. В первом случае получается МА, и Петя, дописав букву К, получает слово МАК из заданного набора и выигрывает. Во втором случае получается МЫ, Петя вынужден дописать Л и Ваня выиграет вторым ходом, дописав О и получив слово МЫЛО.
Пример. Пусть заданы слова {МАК, МЫЛО, РАМА, РАК}. На первом ходу Петя может написать букву М или Р. Пусть он написал букву М. В ответ Ваня может написать А или Ы. В первом случае получается МА, и Петя, дописав букву К, получает слово МАК из заданного набора и выигрывает. Во втором случае получается МЫ, Петя вынужден дописать Л и Ваня выиграет вторым ходом, дописав О и получив слово МЫЛО.
Слайд 23Задача 12. Продолжение
Задание 1.
а) Определите, у кого из игроков
есть выигрышная стратегия для набора слов {ВАРЕНЬЕ, КОРОВА}. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
б) Определите, у кого из игроков есть выигрышная стратегия для набора слов {НУБНУБ…НУБ, PUMAPUMA…PUMA}. В первом слове 55 раз повторяется слово НУБ, а во втором – 32 раза повторяется слово PUMA. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 2
В наборе слов, приведённом в задании 1а, поменяйте местами две буквы в любом слове так, чтобы выигрышная стратегия была у другого игрока. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 3
Дан набор слов {МОРОКА, МОРС, МОРОЗ, ПЛАХА, ПЛАТЬЕ, ПЛОМБА}. У кого из игроков есть выигрышная стратегия? Приведите в виде рисунка или таблицы дерево всех партий, возможных при этой стратегии.
б) Определите, у кого из игроков есть выигрышная стратегия для набора слов {НУБНУБ…НУБ, PUMAPUMA…PUMA}. В первом слове 55 раз повторяется слово НУБ, а во втором – 32 раза повторяется слово PUMA. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 2
В наборе слов, приведённом в задании 1а, поменяйте местами две буквы в любом слове так, чтобы выигрышная стратегия была у другого игрока. Опишите эту стратегию. Определите, сколько различных партий может быть сыграно при этой стратегии и какое слово будет получено в каждом случае.
Задание 3
Дан набор слов {МОРОКА, МОРС, МОРОЗ, ПЛАХА, ПЛАТЬЕ, ПЛОМБА}. У кого из игроков есть выигрышная стратегия? Приведите в виде рисунка или таблицы дерево всех партий, возможных при этой стратегии.
Слайд 24Задача 13.
Два игрока, Петя и Ваня по очереди стирают буквы
из слова или фразы. Первым ходит Петя. За один ход разрешается стереть или ровно одну букву, или все одинаковые буквы. Выигрывает тот, кто сотрёт последнюю букву.
Задание 1. Укажите все слова из списка ниже, начиная с которых выигрывает Петя.
ДА, АГА, СТО, МАМА, СССР, ОГОГО, ТАРТАР, ТОРТ, РОКОКО, РЕННЕР, АВАТАР, КАРАКУРТ, КАСКАД, АНАТАНА, НЯННЯН, НАГАН.
Задание 2. Укажите все слова из представленных, начиная с которых Ваня не может гарантированно выиграть своим первым ходом, но может выиграть либо своим первым или вторым ходом, в зависимости от хода Пети. Для всех выбранных слов укажите его выигрышную стратегию.
Задание 3. Дана фраза: ИНФОРМАТИКА ЭТО НАУКА. Кто выиграет в этой игре, и какой будет выигрышная стратегия этого игрока?
Задание 1. Укажите все слова из списка ниже, начиная с которых выигрывает Петя.
ДА, АГА, СТО, МАМА, СССР, ОГОГО, ТАРТАР, ТОРТ, РОКОКО, РЕННЕР, АВАТАР, КАРАКУРТ, КАСКАД, АНАТАНА, НЯННЯН, НАГАН.
Задание 2. Укажите все слова из представленных, начиная с которых Ваня не может гарантированно выиграть своим первым ходом, но может выиграть либо своим первым или вторым ходом, в зависимости от хода Пети. Для всех выбранных слов укажите его выигрышную стратегию.
Задание 3. Дана фраза: ИНФОРМАТИКА ЭТО НАУКА. Кто выиграет в этой игре, и какой будет выигрышная стратегия этого игрока?
Слайд 25Задача 14.
Два игрока, Петя и Ваня, играют в следующую игру.
Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в кучу один камень или
б) увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче становится не менее 24. Если при этом в куче оказалось не более 38 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче был 21 камень и Петя удвоит количество камней в куче, то игра закончится и победителем будет Ваня. В начальный момент в куче было S камней, 1Задание 1. а) При каких значениях числа S Петя может выиграть в один ход? Укажите все такие значения и соответствующие ходы Пети.
б) У кого из игроков есть выигрышная стратегия при S = 22, 21, 20? Опишите выигрышные стратегии для этих случаев.
Задание 2. У кого из игроков есть выигрышная стратегия при S = 11, 10? Опишите соответствующие выигрышные стратегии.
Задание 3. У кого из игроков есть выигрышная стратегия при S = 9? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.
а) добавить в кучу один камень или
б) увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче становится не менее 24. Если при этом в куче оказалось не более 38 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче был 21 камень и Петя удвоит количество камней в куче, то игра закончится и победителем будет Ваня. В начальный момент в куче было S камней, 1
б) У кого из игроков есть выигрышная стратегия при S = 22, 21, 20? Опишите выигрышные стратегии для этих случаев.
Задание 2. У кого из игроков есть выигрышная стратегия при S = 11, 10? Опишите соответствующие выигрышные стратегии.
Задание 3. У кого из игроков есть выигрышная стратегия при S = 9? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.
Слайд 26Два игрока, Петя и Ваня играют в игру с цепочками символов.
Игра начинается со слова, которое состоит из n букв Ю и m букв Я. Такое слово будем обозначать как (n, m). Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
1) добавить в слово одну букву, Ю или Я
2) удвоить количество букв Ю
3) удвоить количество букв Я
Игра завершается в тот момент, когда длина слова становится не менее 65 символов. Победителем считается игрок, сделавший последний ход, т.е. первым получивший слово длиной 65 или больше.
Задание 1
Для каждой из начальных позиций (6, 29), (8, 28) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2
Для каждой из начальных позиций (6, 28), (7, 28), (8, 27) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 3
Для начальной позиции (5, 28) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
1) добавить в слово одну букву, Ю или Я
2) удвоить количество букв Ю
3) удвоить количество букв Я
Игра завершается в тот момент, когда длина слова становится не менее 65 символов. Победителем считается игрок, сделавший последний ход, т.е. первым получивший слово длиной 65 или больше.
Задание 1
Для каждой из начальных позиций (6, 29), (8, 28) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2
Для каждой из начальных позиций (6, 28), (7, 28), (8, 27) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 3
Для начальной позиции (5, 28) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
Задача 15
Слайд 27. Два игрока, Петя и Ваня, играют в следующую игру. Перед
игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.
Задание 1. Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2. Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 3. Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.
Задание 1. Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2. Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 3. Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.