- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Минимизация булевых функций к элективному курсу Математические основы информатики
Содержание
- 1. Презентация Минимизация булевых функций к элективному курсу Математические основы информатики
- 2. Элементарная дизъюнкция - дизъюнкция переменных или их отрицаний,
- 3. Дизъюнктивная нормальная форма (ДНФ) - формула, имеющая вид
- 4. Совершенная дизъюнктивная нормальная форма (СДНФ) - ДНФ, в
- 5. Алгоритм построения СДНФ F(X,У) = X
- 6. ЗадачаРеализовать булеву функцию с использованием минимального количества
- 7. Способ 1Построение минимальной ДНФ из СДНФ тождественными
- 8. Способ 2Построение минимальной ДНФ из СДНФ методом
- 9. Шаг 1Вычеркнуть из таблицы все строки, в
- 10. Шаг 2Конъюнкции вычеркнутых строк вычеркнуть во всех
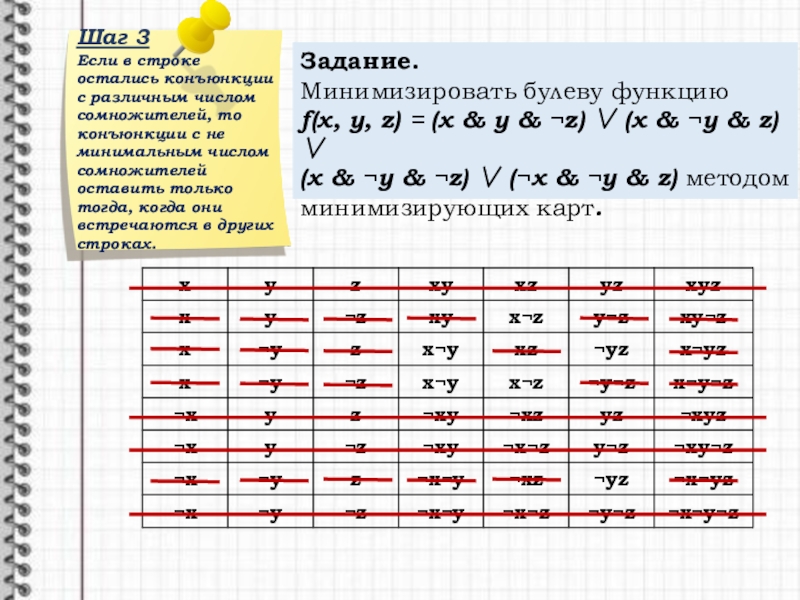
- 11. Шаг 3Если в строке остались конъюнкции с
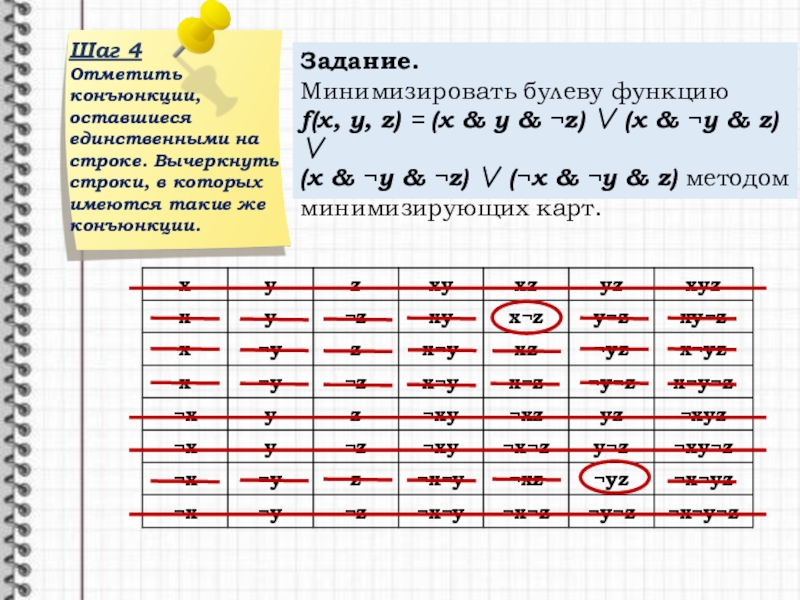
- 12. Шаг 4Отметить конъюнкции, оставшиеся единственными на строке.
- 13. Задание.Минимизировать булеву функцию f(x, y, z) =
- 14. Задание.Минимизировать булеву функцию, заданную вектором f(x, y, z) = (10110011) методом минимизирующих карт.Ответ: y xz.
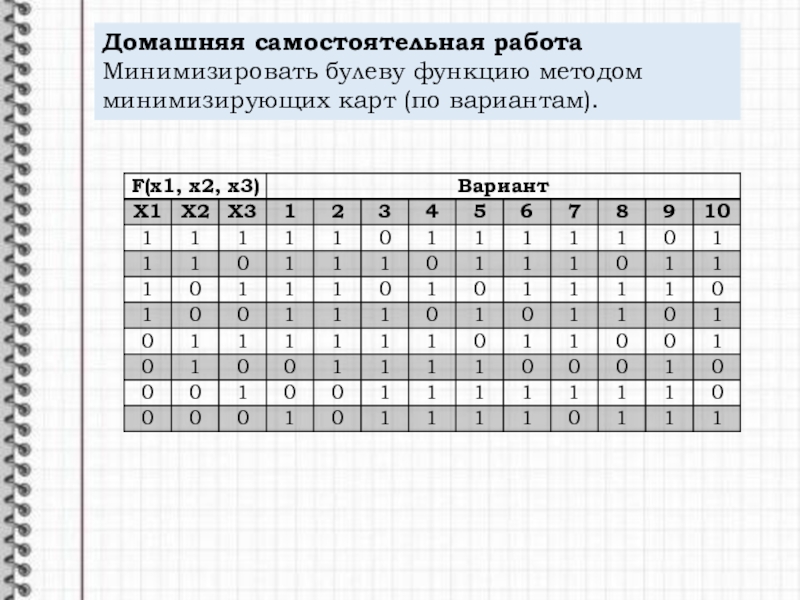
- 15. Домашняя самостоятельная работаМинимизировать булеву функцию методом минимизирующих карт (по вариантам).
Слайд 2Элементарная дизъюнкция - дизъюнкция переменных или их отрицаний, в которой каждая переменная
Элементарная конъюнкция - конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.
Слайд 3Дизъюнктивная нормальная форма (ДНФ) - формула, имеющая вид дизъюнкции элементарных конъюнкций.
Конъюнктивная нормальная
Слайд 4Совершенная дизъюнктивная нормальная форма (СДНФ) - ДНФ, в которой нет одинаковых элементарных
Совершенная конъюнктивная нормальная форма (СКНФ) - КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
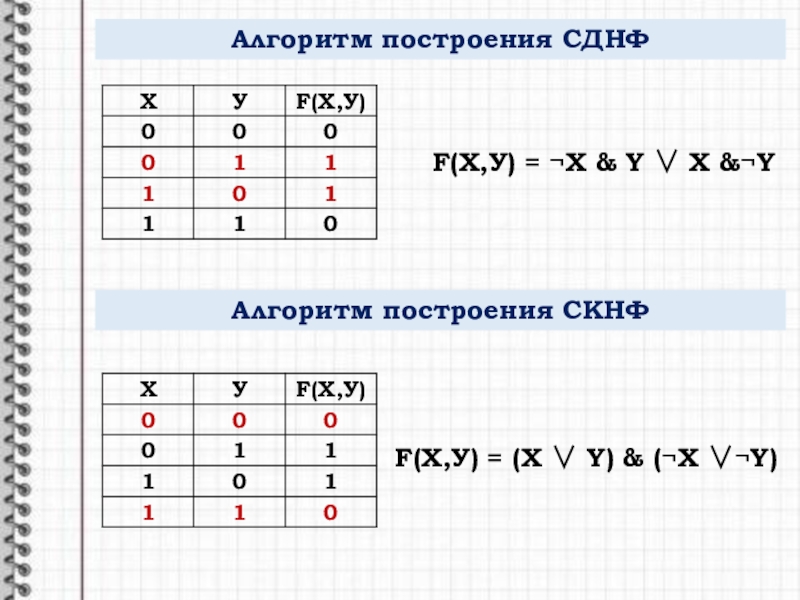
Слайд 5Алгоритм построения СДНФ
F(X,У) = X Y X Y
Алгоритм
F(X,У) = (X Y) (X Y)
Слайд 6Задача
Реализовать булеву функцию с использованием минимального количества логических элементов.
Минимизация булевых функций
ДНФ называется минимальной, если она содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.
Процесс нахождения минимальной ДНФ называется минимизацией в классе ДНФ.
Слайд 7Способ 1
Построение минимальной ДНФ из СДНФ тождественными преобразованиями.
Задание.
Минимизировать булеву функцию
f(x,
(x y z) (x y z).
f(x, y, z) = (x y z) (x y z) (x y z) (x y z) =
= x z (y y) y z (x x) =
= x z y z
!
Для нахождения минимальной ДНФ необходимо перебрать все возможные способы применения законов алгебры логики к исходной формуле.
Слайд 8Способ 2
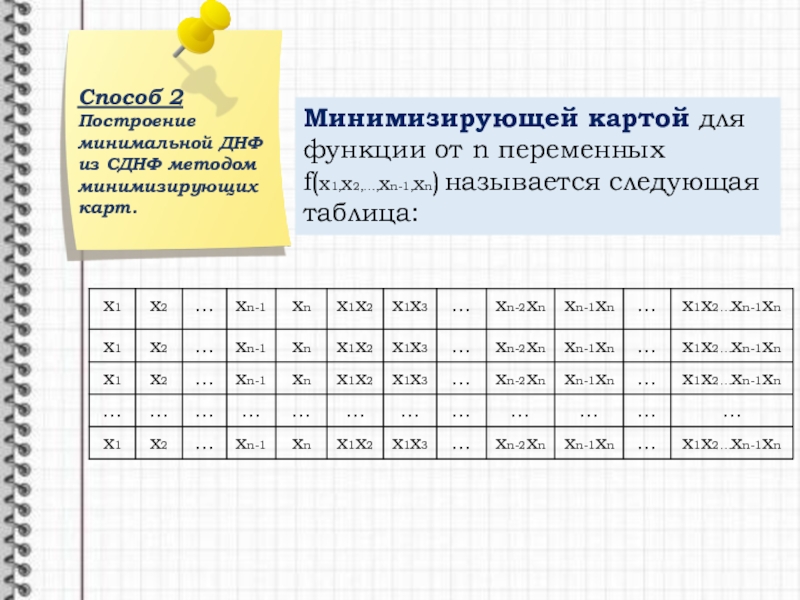
Построение минимальной ДНФ из СДНФ методом минимизирующих карт.
Минимизирующей картой для
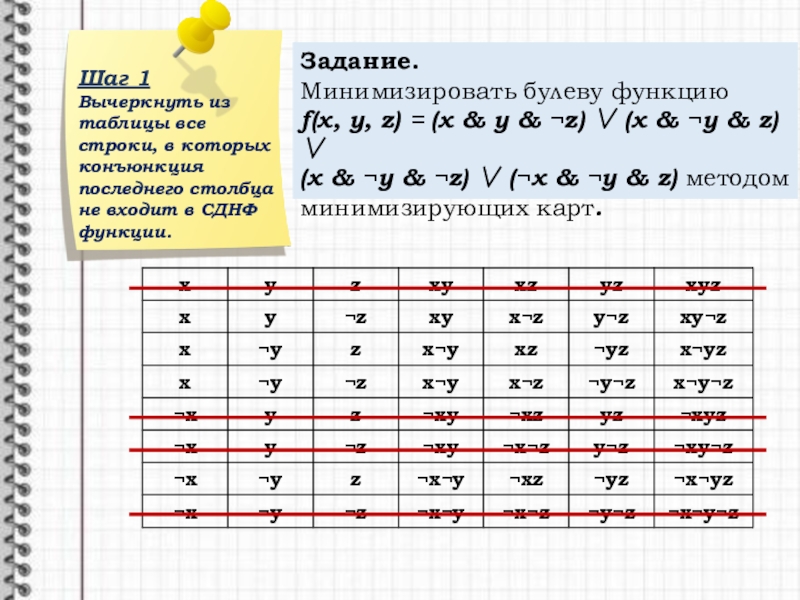
Слайд 9Шаг 1
Вычеркнуть из таблицы все строки, в которых конъюнкция последнего столбца
Задание.
Минимизировать булеву функцию
f(x, y, z) = (x y z) (x y z)
(x y z) (x y z) методом минимизирующих карт.
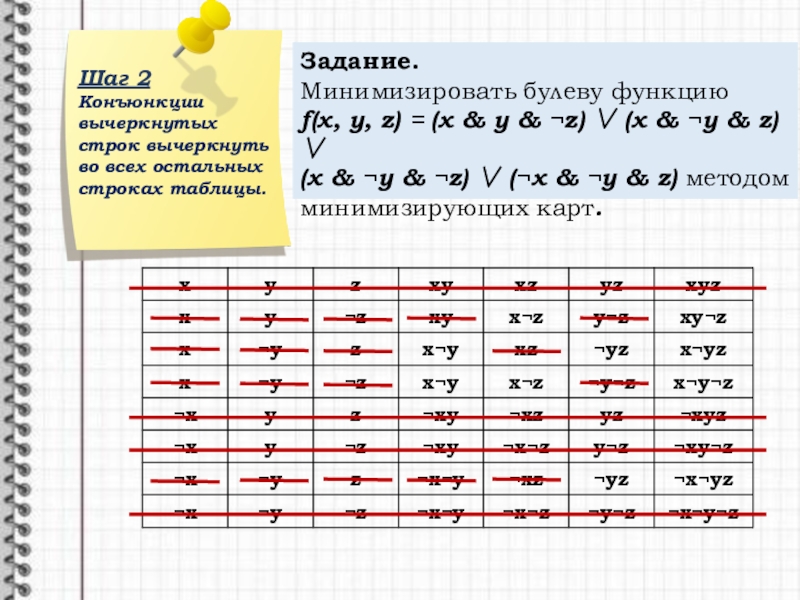
Слайд 10Шаг 2
Конъюнкции вычеркнутых строк вычеркнуть во всех остальных строках таблицы.
Задание.
Минимизировать булеву
f(x, y, z) = (x y z) (x y z)
(x y z) (x y z) методом минимизирующих карт.
Слайд 11Шаг 3
Если в строке остались конъюнкции с различным числом сомножителей, то
Задание.
Минимизировать булеву функцию
f(x, y, z) = (x y z) (x y z)
(x y z) (x y z) методом минимизирующих карт.
Слайд 12Шаг 4
Отметить конъюнкции, оставшиеся единственными на строке. Вычеркнуть строки, в которых
Задание.
Минимизировать булеву функцию
f(x, y, z) = (x y z) (x y z)
(x y z) (x y z) методом минимизирующих карт.
Слайд 13Задание.
Минимизировать булеву функцию
f(x, y, z) = (x y
(x y z) (x y z) методом минимизирующих карт.
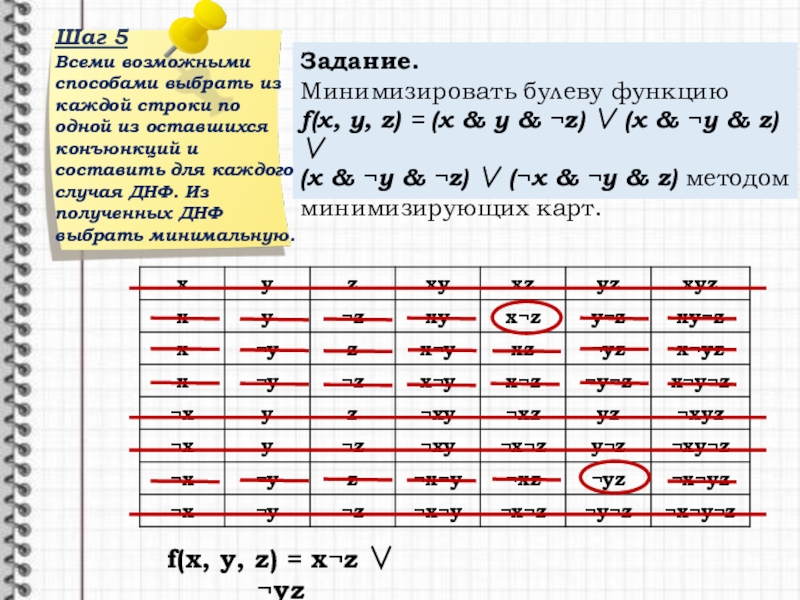
Шаг 5
Всеми возможными способами выбрать из каждой строки по одной из оставшихся конъюнкций и составить для каждого случая ДНФ. Из полученных ДНФ выбрать минимальную.
f(x, y, z) = xz yz
Слайд 14Задание.
Минимизировать булеву функцию, заданную вектором
f(x, y, z) = (10110011) методом
Ответ: y xz.
Слайд 15Домашняя самостоятельная работа
Минимизировать булеву функцию методом минимизирующих карт (по вариантам).
