- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Круги Эйлера для проведения факультативных занятий Занимательная информатика в 5 классе.
Содержание
- 1. Презентация Круги Эйлера для проведения факультативных занятий Занимательная информатика в 5 классе.
- 2. Леонард Эйлер Леонард Эйлер, крупнейший математик
- 3. С1761 по 1768 год им были написаны
- 4. После Эйлера этот же метод разрабатывал чешский
- 5. Круги ЭЙЛЕРА — геометрическая схема, с помощью
- 6. Круги Эйлера Это новый тип задач,
- 7. Типы кругов Эйлера
- 8. Решение логических задач с помощью кругов Эйлера
- 9. ЗадачаКаждый из 35 шестиклассников является читателем, по
- 10. Круги ЭйлераХодят только школьную библиотеку Ходят в
- 11. Задача: Из 100
- 12. Всеми тремя языками владеют три туриста, значит,
- 13. немецкийфранцузскийанглийский375Известно, что немецким языком владеют 30 человек,
- 14. В одной семье было много детей. 7
- 15. Решите самостоятельно
- 16. ВыводыПрименение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко
Слайд 2Леонард Эйлер
Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В
Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер (1707 – 1783).
(1707 г.-1783 г.)
Слайд 3С1761 по 1768 год им были написаны знаменитые «Письма к немецкой
Слайд 4После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781
Слайд 5 Круги ЭЙЛЕРА — геометрическая схема, с помощью которой можно изобразить отношения
Слайд 6
Круги Эйлера
Это новый тип задач, в которых требуется найти
Слайд 9Задача
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из
Сколько шестиклассников являются читателями обеих библиотек?
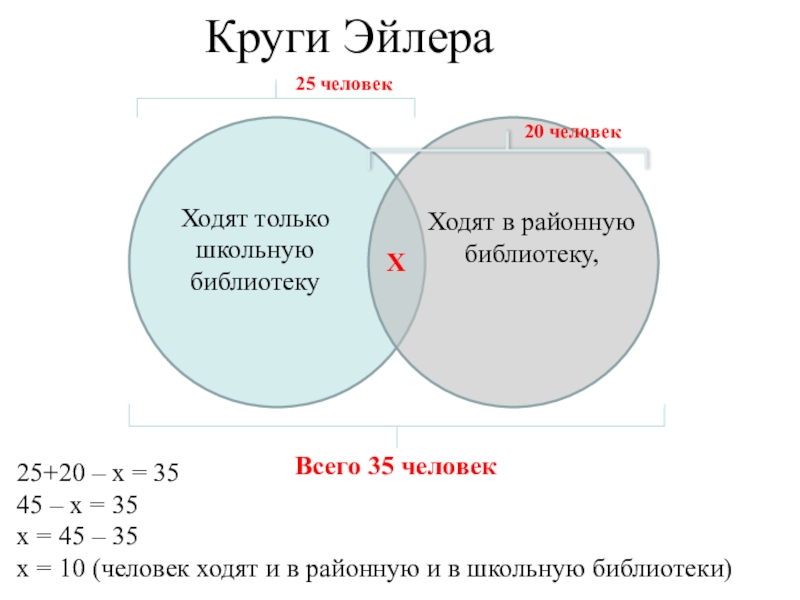
Слайд 10Круги Эйлера
Ходят только школьную библиотеку
Ходят в районную библиотеку,
Всего 35
Х
25+20 – х = 35
45 – х = 35
х = 45 – 35
х = 10 (человек ходят и в районную и в школьную библиотеки)
25 человек
20 человек
Слайд 11 Задача:
Из 100 туристов, отправляющихся в заграничное
Сколько туристов не владеют ни одним языком?
Решение:
Выразим условие задачи графически. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знают немецкий.
французский
немецкий
английский
Слайд 12Всеми тремя языками владеют три туриста, значит, в общей части кругов
3
Английским и французским языками владеют 10 человек, а 3 из них владеют ещё и немецким. Значит, английским и французским владеют 10-3=7 человек.
немецкий
французский
английский
В общую часть английского и французского кругов вписываем цифру 7.
7
Английским и немецким языками владеют 8 человек, а 3 из них владеют ещё и французским. Значит, английским и немецким владеют 8-3=5 человек.
В общую часть английского и немецкого кругов вписываем число 5.
5
Слайд 13немецкий
французский
английский
3
7
5
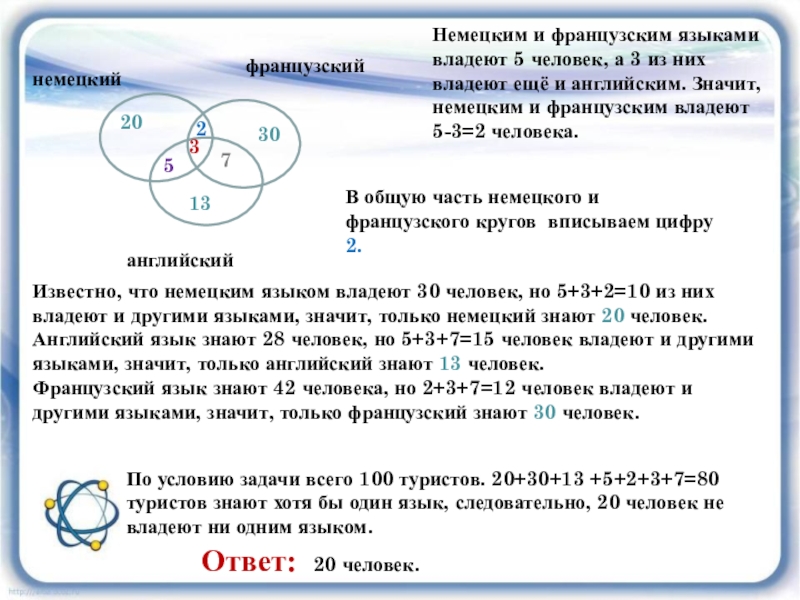
Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них
Английский язык знают 28 человек, но 5+3+7=15 человек владеют и другими языками, значит, только английский знают 13 человек.
Французский язык знают 42 человека, но 2+3+7=12 человек владеют и другими языками, значит, только французский знают 30 человек.
Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека.
В общую часть немецкого и французского кругов вписываем цифру 2.
2
20
13
30
По условию задачи всего 100 туристов. 20+30+13 +5+2+3+7=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним языком.
Ответ: 20 человек.
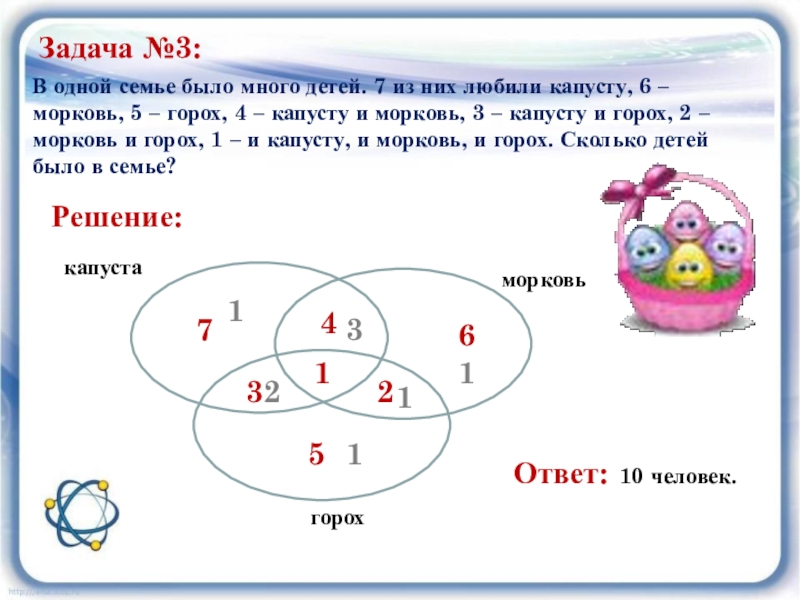
Слайд 14В одной семье было много детей. 7 из них любили капусту,
Задача №3:
Решение:
капуста
морковь
горох
7
6
5
4
3
2
1
3
2
1
1
1
1
Ответ: 10 человек.