- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Циклический алгоритм
Содержание
- 1. Презентация к уроку Циклический алгоритм
- 2. Алгоритм называется циклическим, если в нем имеются
- 3. Цикл с постусловием Проверка условия выполняется после первой обработки тела цикла и контролирует выход из него.
- 4. Задача 1. Составить алгоритм вывода двузначных
- 5. Матем. модель:начальное значение Х равно 0. Ввод
- 6. Псевдокод1. Начальное значение x:=02. Начало цикла Пока x
- 7. конецX:=X+10началоХ
- 8. ЗАДАНИЕ №2. Составить алгоритм расчет суммы
- 9. Матем. модель:введем конечное число расчета суммы n;зададим
- 10. конецI:=I+1началоI
- 11. Цикл с предусловием В таких циклических алгоритмах
- 12. ЗАДАНИЕ №3. Составить блок-схему алгоритма алгоритма вывода
- 13. Матем. модель: алгоритм будет выполняться до тех
- 14. конецначалоS
- 15. ЗАДАНИЕ №4. Составить блок-схему алгоритма алгоритма вывода
- 16. Матем. модель: задаем начальное значение базовой переменной
- 17. конецх:=х+1началох
- 18. Безусловный циклОбычно используется в алгоритмах, когда нужное
- 19. ЗАДАНИЕ №5. Составить блок-схему алгоритма вычисления суммы
- 20. Математическая модель: выражение представляет собой закономерную последовательность,
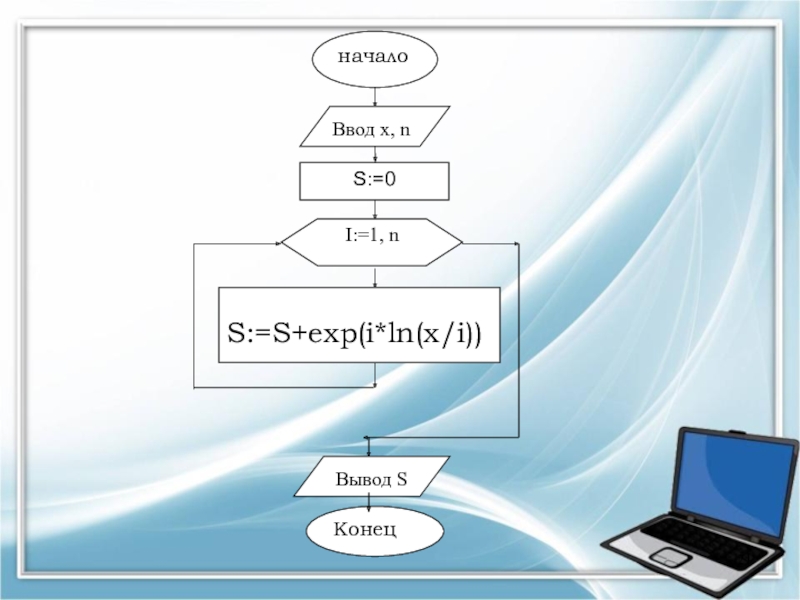
- 21. началоКонецS:=0Вывод SВвод x, nI:=1, nS:=S+exp(i*ln(x/i))
- 22. Решение задач№1 Составить псевдокод алгоритма вычисления квадратов
- 23. Самостоятельная работа 1. Составить алгоритм вычисления произведения
Алгоритм называется циклическим, если в нем имеются действия или наборы действий, которые необходимо выполнить более одного раза. Повторяющиеся алгоритмические действия являются телом цикла. Дополнительно каждый цикл имеет условие, по которому выполнение циклического алгоритма заканчивается.
Слайд 2Алгоритм называется циклическим, если в нем имеются действия или наборы действий,
которые необходимо выполнить более одного раза.
Повторяющиеся алгоритмические действия являются телом цикла.
Дополнительно каждый цикл имеет условие, по которому выполнение циклического алгоритма заканчивается.
Повторяющиеся алгоритмические действия являются телом цикла.
Дополнительно каждый цикл имеет условие, по которому выполнение циклического алгоритма заканчивается.
Слайд 3Цикл с постусловием
Проверка условия выполняется после первой обработки тела цикла
и контролирует выход из него.
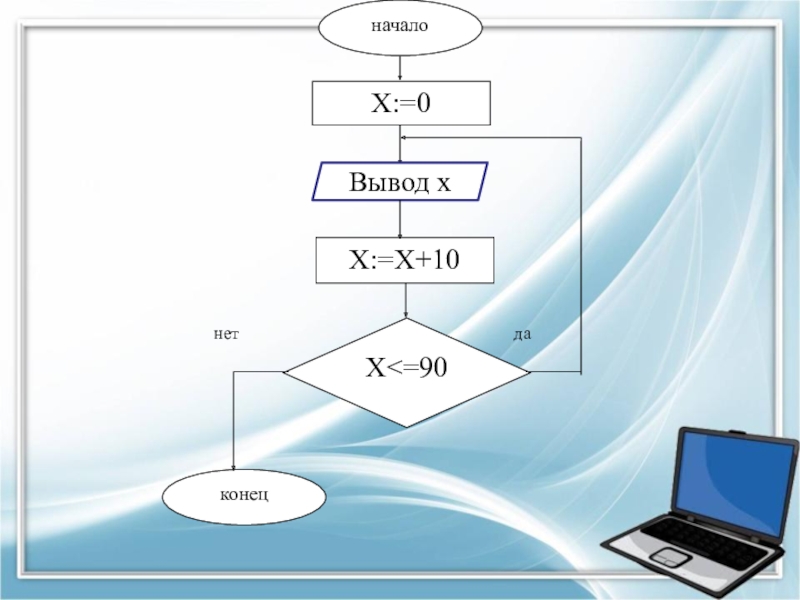
Слайд 4Задача 1. Составить алгоритм вывода двузначных чисел, оканчивающихся на 0.
Постановка
задачи:
Вх. данные: х - число
Вых. данные: х – число
Вх. данные: х - число
Вых. данные: х – число
Слайд 5Матем. модель:
начальное значение Х равно 0. Ввод значения Х выполняется командой
присваивания: х:=0.
т.к. первое двузначное число, оканчивающееся нулём – это число 10, выполним действие Х=Х+10,
далее Х примет значение 20, затем 30, …, 90.
Значит, переменная X изменяет своё значение на промежутке от 10 до 90 с шагом 10.
Результатом является значение величины X на каждом повторении цикла.
т.к. первое двузначное число, оканчивающееся нулём – это число 10, выполним действие Х=Х+10,
далее Х примет значение 20, затем 30, …, 90.
Значит, переменная X изменяет своё значение на промежутке от 10 до 90 с шагом 10.
Результатом является значение величины X на каждом повторении цикла.
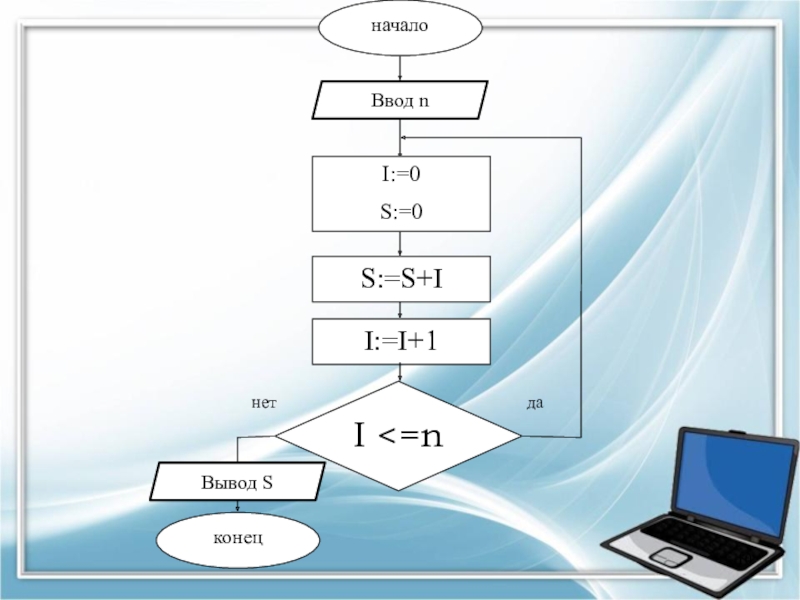
Слайд 8ЗАДАНИЕ №2. Составить алгоритм расчет суммы от 1 до числа
n.
Вх. данные: n – натуральное чичло
Вых. данные: S
Вх. данные: n – натуральное чичло
Вых. данные: S
Слайд 9Матем. модель:
введем конечное число расчета суммы n;
зададим нулевые начальные значения итоговой
суммы S (S:=0) и счетчика цикла I (I:=0);
циклический процесс выполняется до первой проверки условия (S:=S+I, I:=I+1);
проверим условие цикла, т. е. значение счетчика I меньше или равен n (I <=n). Если результат условия положительный, выполняем цикл еще раз, иначе заканчиваем цикл и выводим сумму на дисплей или печать.
циклический процесс выполняется до первой проверки условия (S:=S+I, I:=I+1);
проверим условие цикла, т. е. значение счетчика I меньше или равен n (I <=n). Если результат условия положительный, выполняем цикл еще раз, иначе заканчиваем цикл и выводим сумму на дисплей или печать.
Слайд 11Цикл с предусловием
В таких циклических алгоритмах условие продолжения проверяется до
обработки тела цикла, т. е. наличествует необходимость повторения обработки цикла.
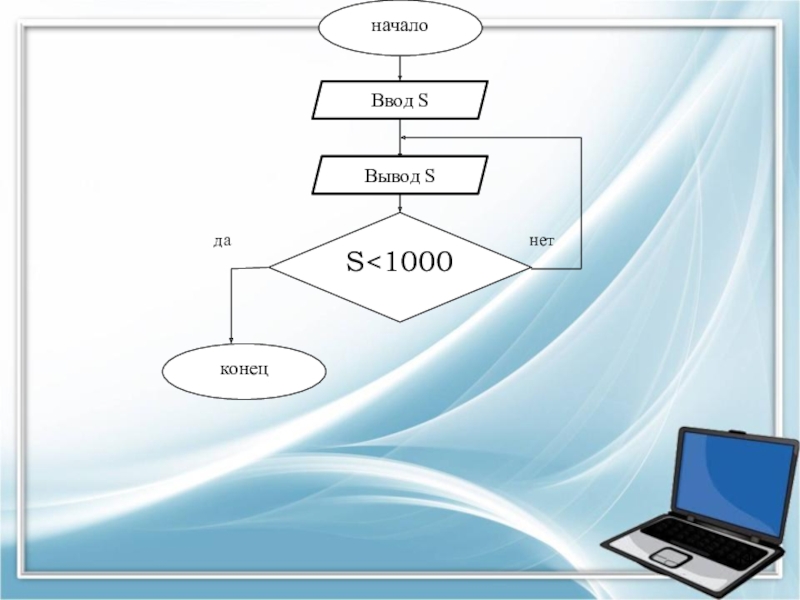
Слайд 12ЗАДАНИЕ №3. Составить блок-схему алгоритма алгоритма вывода стоимости товаров в чеке
до первой суммы, превышающей 1000 руб.
Постановка задачи:
Входные данные: S (стоимость);
Выходные данные: S.
Постановка задачи:
Входные данные: S (стоимость);
Выходные данные: S.
Слайд 13Матем. модель: алгоритм будет выполняться до тех пор, пока не будет
введена первая сумма, превышающая 1000 руб.
Псевдокод
1. Начало цикла
Выполнять:
Ввод S
Вывод S
До
Проверка условия:
S<1000
Конец цикла
2. Конец
Псевдокод
1. Начало цикла
Выполнять:
Ввод S
Вывод S
До
Проверка условия:
S<1000
Конец цикла
2. Конец
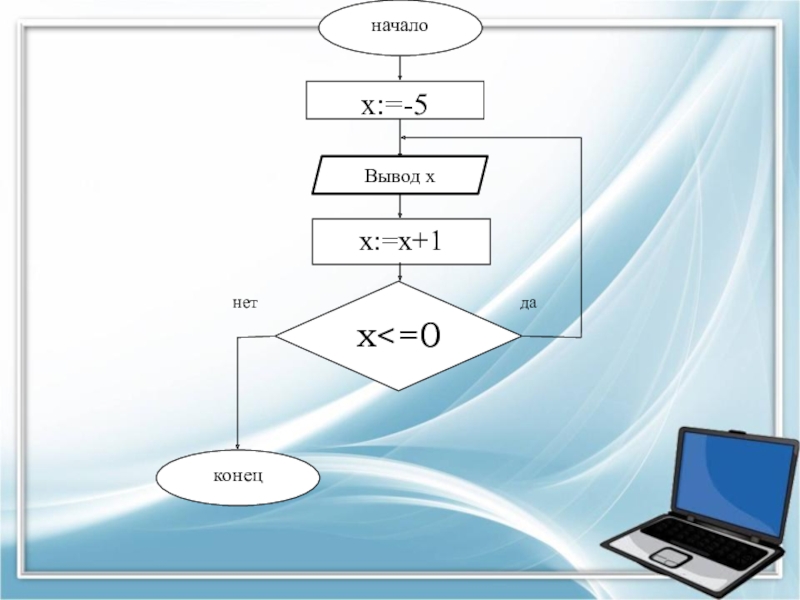
Слайд 15ЗАДАНИЕ №4. Составить блок-схему алгоритма алгоритма вывода на печать чисел от
-5 до 0.
Постановка задачи:
Входные данные: x - число
Выходные данные: x
Постановка задачи:
Входные данные: x - число
Выходные данные: x
Слайд 16Матем. модель:
задаем начальное значение базовой переменной j, равное -5;
проверяем условие
цикла, условие положительное, и тело цикла выполняется первый раз;
далее прибавляем к переменной j единицу, снова проверяем условие цикла;
цикл продолжает выполняться, пока значение j меньше нуля или равно ему, в противном случае выходим из цикла по ветке
далее прибавляем к переменной j единицу, снова проверяем условие цикла;
цикл продолжает выполняться, пока значение j меньше нуля или равно ему, в противном случае выходим из цикла по ветке
Слайд 18Безусловный цикл
Обычно используется в алгоритмах, когда нужное количество выполнений цикла заранее
известно, и очень часто применяется при работе с массивами.
Такой алгоритм содержит три обязательных элемента: стартовое значение, которое называют параметром цикла, т. к. именно эта переменная изменяется после каждого выполнения цикла и определяет момент его завершения значение, при котором цикл завершается.
В таких циклических алгоритмах условие продолжения проверяется до обработки тела цикла, т. е. наличествует необходимость повторения обработки цикла.
Такой алгоритм содержит три обязательных элемента: стартовое значение, которое называют параметром цикла, т. к. именно эта переменная изменяется после каждого выполнения цикла и определяет момент его завершения значение, при котором цикл завершается.
В таких циклических алгоритмах условие продолжения проверяется до обработки тела цикла, т. е. наличествует необходимость повторения обработки цикла.
Слайд 19ЗАДАНИЕ №5. Составить блок-схему алгоритма вычисления суммы n первых членов ряда
Постановка задачи:
Входные данные: x, n - число
Выходные данные: S – сумма
Слайд 20Математическая модель:
выражение представляет собой закономерную последовательность, все члены которой изменяются
по одному закону:
первый , второй , третий .
Введём переменной I обозначение показателя степеней, основания ступени в знаменателе дроби.
Выведем формулу последовательности: , где i изменяется от 1 до n. Формула нахождения суммы:
первый , второй , третий .
Введём переменной I обозначение показателя степеней, основания ступени в знаменателе дроби.
Выведем формулу последовательности: , где i изменяется от 1 до n. Формула нахождения суммы:
Слайд 22Решение задач
№1 Составить псевдокод алгоритма вычисления квадратов чисел, заданных на промежутке
Выполнить исполнение алгоритма для n=5.
№2 Даны 50 концентрических окружностей, радиус каждой отчается на 3 см. Вычислить и напечатать радиус наибольшей окружности. Составить псевдокод.
Пояснение: некоторая переменная I изменяет своё значение на промежутке [1,50]. А радиус для каждой новой окружности вычисляется по формуле r=r+3.
№2 Даны 50 концентрических окружностей, радиус каждой отчается на 3 см. Вычислить и напечатать радиус наибольшей окружности. Составить псевдокод.
Пояснение: некоторая переменная I изменяет своё значение на промежутке [1,50]. А радиус для каждой новой окружности вычисляется по формуле r=r+3.
Слайд 23Самостоятельная работа
1. Составить алгоритм вычисления произведения 100 натуральных чисел.
2.
Составить алгоритм вычисления суммы чётных чисел из промежутка [10, 20].
3. Составить алгоритм вычисления стоимости покупки с учетом скидки: при покупке товара на сумму больше 500 руб. предоставляется скидка 10 %. Входные данные: a (цена единицы товара), b (количество единиц товара); выходные данные: s (сумма покупки).
4. Составить алгоритм вычисления значения функции y=cos(x+1) при значениях х от -20 до 20 с шагом изменения 0,5.
3. Составить алгоритм вычисления стоимости покупки с учетом скидки: при покупке товара на сумму больше 500 руб. предоставляется скидка 10 %. Входные данные: a (цена единицы товара), b (количество единиц товара); выходные данные: s (сумма покупки).
4. Составить алгоритм вычисления значения функции y=cos(x+1) при значениях х от -20 до 20 с шагом изменения 0,5.