имени П.М.Вострухина
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по Информатике на тему: Использование метода кругов Эйлера для решения задач поиска информации
Содержание
- 1. Презентация к уроку по Информатике на тему: Использование метода кругов Эйлера для решения задач поиска информации
- 2. Содержание Введение Представление логических связок в поисковых
- 3. Круги Эйлера Круги Эйлера — геометрическая схема,
- 4. Круги Эйлера Достаточно основательно развил этот метод
- 5. Представление логических связок При
- 6. Связь логических операций с теорией множеств
- 7. Использование кругов Эйлера при доказательстве логических
- 8. Использование кругов Эйлера при доказательстве логических
- 9. Задачи в формате ГИА и ЕГЭ по теме: «Поиск информации в Интернет»
- 10. Задача №18 из демо-версии ГИА
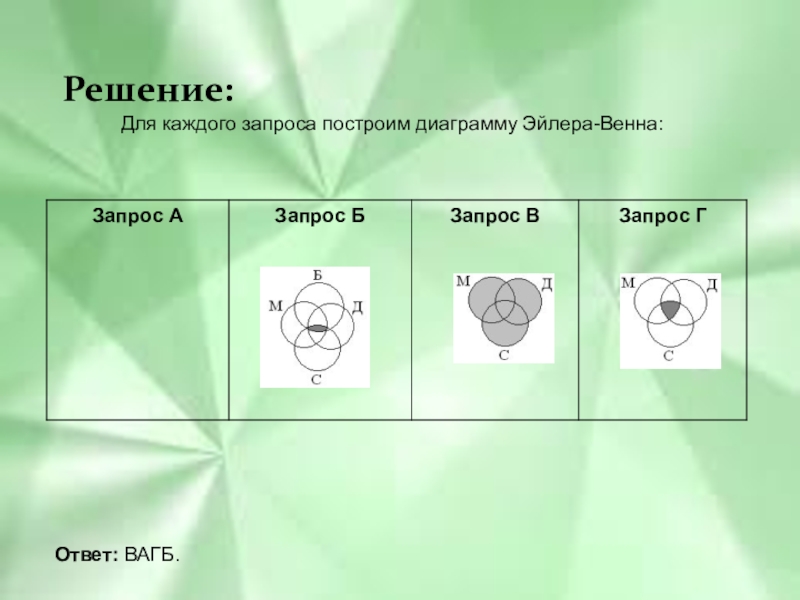
- 11. Решение: Для каждого запроса построим диаграмму Эйлера-Венна:Ответ: ВАГБ.
- 12. Задача В12 из демо-версии ЕГЭ-2013 В таблице
- 13. Решение: Пусть Ф – количество страниц (в
Содержание Введение Представление логических связок в поисковых запросах Связь логических операций с теорией множеств Использование кругов Эйлера при доказательстве логических равенств Задачи в формате ГИА и ЕГЭ по теме: «Поиск информации в Интернете»
Слайд 2Содержание
Введение
Представление логических связок в поисковых запросах
Связь логических операций
с теорией множеств
Использование кругов Эйлера при доказательстве логических равенств
Задачи в формате ГИА и ЕГЭ по теме: «Поиск информации в Интернете»
Использование кругов Эйлера при доказательстве логических равенств
Задачи в формате ГИА и ЕГЭ по теме: «Поиск информации в Интернете»
Слайд 3 Круги Эйлера
Круги Эйлера — геометрическая схема, с помощью которой можно
изобразить отношения между подмножествами, для наглядного
представления. Изобретены Леонардом Эйлером. Используется в
математике, логике, менеджменте и других прикладных направлениях.
Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна,
изображающие все комбинаций свойств, то есть конечную булеву
алгебру. При диаграмма Эйлера — Венна обычно изображается в виде
трёх кругов с центрами в вершинах равностороннего треугольника и
одинаковым радиусом, приблизительно равным длине стороны
треугольника.
При решении целого ряда задач Леонард Эйлер использовал идею
изображения множеств с помощью кругов. Однако этим методом ещё до
Эйлера пользовался выдающийся немецкий философ и математик
Готфрид Вильгельм Лейбниц. Лейбниц использовал их для
геометрической интерпретации логических связей между понятиями, но
при этом всё же предпочитал использовать линейные схемы.
Слайд 4 Круги Эйлера
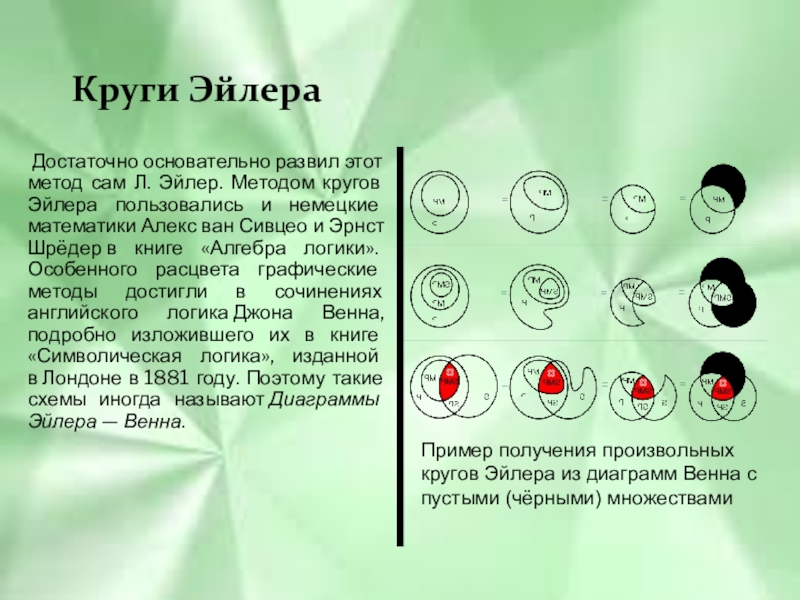
Достаточно основательно развил этот метод сам Л. Эйлер. Методом
кругов Эйлера пользовались и немецкие математики Алекс ван Сивцео и Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами
Слайд 5Представление логических связок
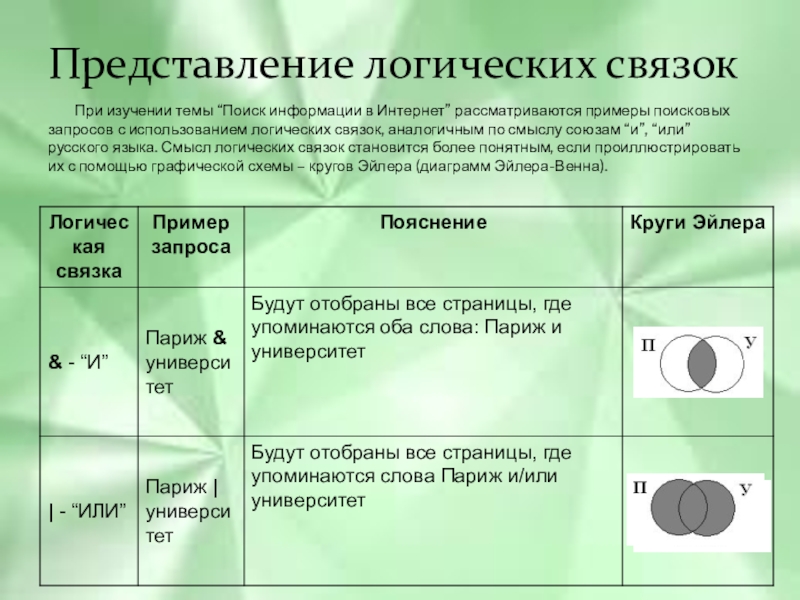
При изучении темы “Поиск информации
в Интернет” рассматриваются примеры поисковых
запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или”
русского языка. Смысл логических связок становится более понятным, если проиллюстрировать
их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или”
русского языка. Смысл логических связок становится более понятным, если проиллюстрировать
их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
Слайд 6Связь логических операций с теорией множеств
С помощью диаграмм
Эйлера-Венна можно наглядно представить связь
логических операций с теорией множеств. Для демонстрации можно
воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В
Приложении 2 подробно рассматриваются графические иллюстрации
логических операций вместе с их таблицами истинности. Поясним принцип
построения диаграммы в общем случае. На диаграмме – область круга с
именем А отображает истинность высказывания А (в теории множеств круг А
– обозначение всех элементов, входящих в данное множество).
Соответственно, область вне круга отображает значение “ложь”
соответствующего высказывания. Что бы понять какая область диаграммы
будет отображением логической операции нужно заштриховать только те
области, в которых значения логической операции на наборах A и B равны
“истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11).
Заштрихуем последовательно: 1) область вне двух пересекающихся кругов,
которая соответствует значениям А=0, В=0; 2) область, относящуюся только к
кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область,
относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям
А=1, В=1. Объединение этих трех областей и будет графическим
представлением логической операции импликации.
логических операций с теорией множеств. Для демонстрации можно
воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В
Приложении 2 подробно рассматриваются графические иллюстрации
логических операций вместе с их таблицами истинности. Поясним принцип
построения диаграммы в общем случае. На диаграмме – область круга с
именем А отображает истинность высказывания А (в теории множеств круг А
– обозначение всех элементов, входящих в данное множество).
Соответственно, область вне круга отображает значение “ложь”
соответствующего высказывания. Что бы понять какая область диаграммы
будет отображением логической операции нужно заштриховать только те
области, в которых значения логической операции на наборах A и B равны
“истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11).
Заштрихуем последовательно: 1) область вне двух пересекающихся кругов,
которая соответствует значениям А=0, В=0; 2) область, относящуюся только к
кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область,
относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям
А=1, В=1. Объединение этих трех областей и будет графическим
представлением логической операции импликации.
Слайд 7Использование кругов Эйлера при доказательстве
логических равенств
Для того, чтобы доказать
логические равенства можно применить метод
диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) =
¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним
последовательно: заштрихуем оба круга (применим дизъюнкцию)
серым цветом, затем для отображения инверсии заштрихуем область за
пределами кругов черным цветом:
диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) =
¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним
последовательно: заштрихуем оба круга (применим дизъюнкцию)
серым цветом, затем для отображения инверсии заштрихуем область за
пределами кругов черным цветом:
Слайд 8Использование кругов Эйлера при доказательстве
логических равенств
Для визуального представления правой
части равенства
выполним последовательно: заштрихуем область для
отображения инверсии (¬А) серым цветом и, аналогично,
Область (¬В) также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
выполним последовательно: заштрихуем область для
отображения инверсии (¬А) серым цветом и, аналогично,
Область (¬В) также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
Слайд 10
Задача №18 из демо-версии
ГИА 2013
В таблице приведены запросы к
поисковому
серверу. Для
каждого запроса указан его код
– соответствующая буква от А
до Г. Расположите коды
запросов слева направо в
порядке убывания количества
страниц, которые найдет
поисковый сервер по каждому
запросу.
каждого запроса указан его код
– соответствующая буква от А
до Г. Расположите коды
запросов слева направо в
порядке убывания количества
страниц, которые найдет
поисковый сервер по каждому
запросу.
Слайд 12Задача В12 из демо-версии ЕГЭ-2013
В таблице приведены запросы
и количество
найденных по ним
страниц некоторого сегмента
сети Интернет.
Какое количество страниц (в
тысячах) будет найдено по
запросу Эсминец?
Считается, что все запросы
выполнялись практически
одновременно, так что набор
страниц, содержащих все
искомые слова, не изменялся
за время выполнения запросов.
страниц некоторого сегмента
сети Интернет.
Какое количество страниц (в
тысячах) будет найдено по
запросу Эсминец?
Считается, что все запросы
выполнялись практически
одновременно, так что набор
страниц, содержащих все
искомые слова, не изменялся
за время выполнения запросов.
Слайд 13Решение:
Пусть
Ф – количество страниц (в тысячах) по запросу
Фрегат;
Э
– количество страниц (в тысячах) по запросу
Эсминец;
Х – количество страниц (в тысячах) по
запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по
запросу, в котором упоминается Эсминец и не упоминается Фрегат.
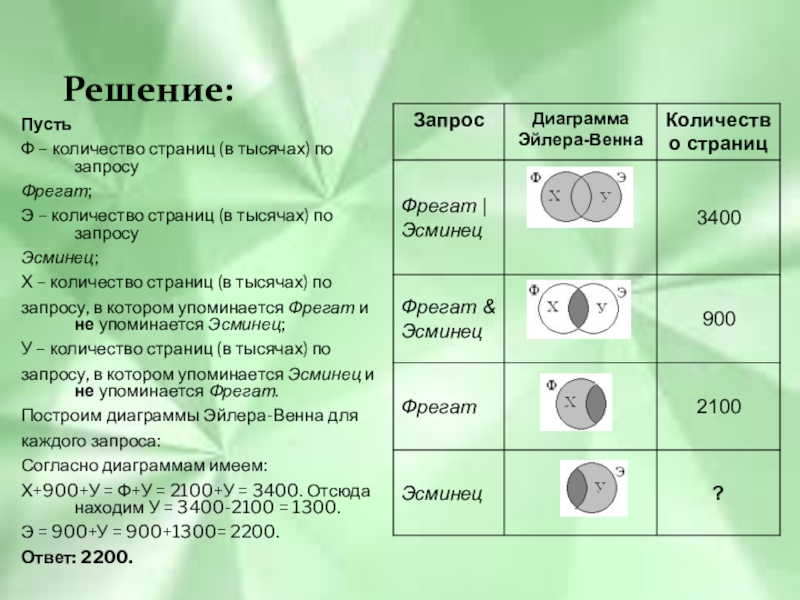
Построим диаграммы Эйлера-Венна для
каждого запроса:
Согласно диаграммам имеем:
Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
Э = 900+У = 900+1300= 2200.
Ответ: 2200.
Эсминец;
Х – количество страниц (в тысячах) по
запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по
запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для
каждого запроса:
Согласно диаграммам имеем:
Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
Э = 900+У = 900+1300= 2200.
Ответ: 2200.